【空间辨识】一致模态指标与模态参与因子的随机子空间辨识研究（Matlab代码实现）

   💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥第一部分——内容介绍

一致模态指标与模态参与因子的随机子空间辨识研究

摘要

本文提出了一种基于随机子空间辨识（SSI）的模态参数估计方法，重点研究了一致模态指标（CMI）与模态参与因子的计算方法。该方法不依赖MATLAB系统辨识工具箱中的n4sid函数，通过构建Hankel矩阵并利用奇异值分解实现状态空间模型的辨识。通过数值仿真验证了算法对含噪声的2自由度系统的有效性，结果表明该方法能准确估计系统模态参数并有效评估模态质量。

关键词

随机子空间辨识；模态分析；一致模态指标；模态参与因子；Hankel矩阵

1 引言

结构健康监测和模态分析在航空航天、土木工程等领域具有重要应用价值。随机子空间辨识（Stochastic Subspace Identification, SSI）作为输出-only模态分析方法，因其无需输入激励信息而得到广泛应用。本文提出一种改进的SSI算法，重点研究一致模态指标（Consistent Modal Indicator, CMI）和模态参与因子（Modal Participation Factor）的计算方法，为模态验证和结构动态特性分析提供更可靠的指标。

2 理论基础

2.1 随机子空间辨识原理

考虑离散状态空间模型：

通过构建过去和未来的Hankel矩阵：

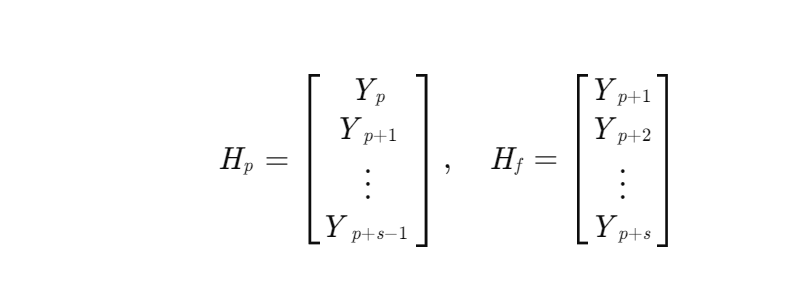
其中Yi​为输出数据块，通过QR分解和奇异值分解可得到状态序列估计。

2.2 模态参数估计

从状态空间矩阵A和C可得到连续系统矩阵：

2.3 一致模态指标(CMI)

CMI用于评估模态估计的一致性，定义为：

2.4 模态参与因子

参与因子表示各状态变量对特定模态的贡献程度：

3 算法实现

3.1 主要步骤

1. 数据预处理：去除均值，可选滤波处理
2. Hankel矩阵构建：根据输入参数确定矩阵维度
3. QR分解：实现数据压缩
4. 奇异值分解：确定系统阶数
5. 状态空间实现：计算A和C矩阵
6. 模态参数提取：特征值分解得到模态参数
7. 指标计算：计算EMAC、MPC、CMI和参与因子

3.2 函数语法说明

matlab

1function [Result] = SSID(output, fs, ncols, nrows, cut)
2% 输入参数：
3%   output - 输出数据矩阵(输出通道数×数据点数)
4%   fs - 采样频率(Hz)
5%   ncols - Hankel矩阵列数(建议>2/3数据点数)
6%   nrows - Hankel矩阵行数(建议>20×模态阶数)
7%   cut - 截断值(取2×模态阶数)
8%
9% 输出参数：
10%   Result - 包含模态参数和指标的结构体
11%     Parameters.NaFreq - 自然频率向量(rad/s)
12%     Parameters.DampRatio - 阻尼比向量
13%     Parameters.ModeShape - 模态振型矩阵
14%     Indicators.EMAC - 扩展模态幅值相干系数
15%     Indicators.MPC - 模态相位共线性
16%     Indicators.CMI - 一致模态指标
17%     Indicators.partfac - 参与因子
18%     Matrices.A, C - 离散状态空间矩阵
19end

4 数值仿真

4.1 2自由度系统模型

考虑质量-弹簧-阻尼系统：

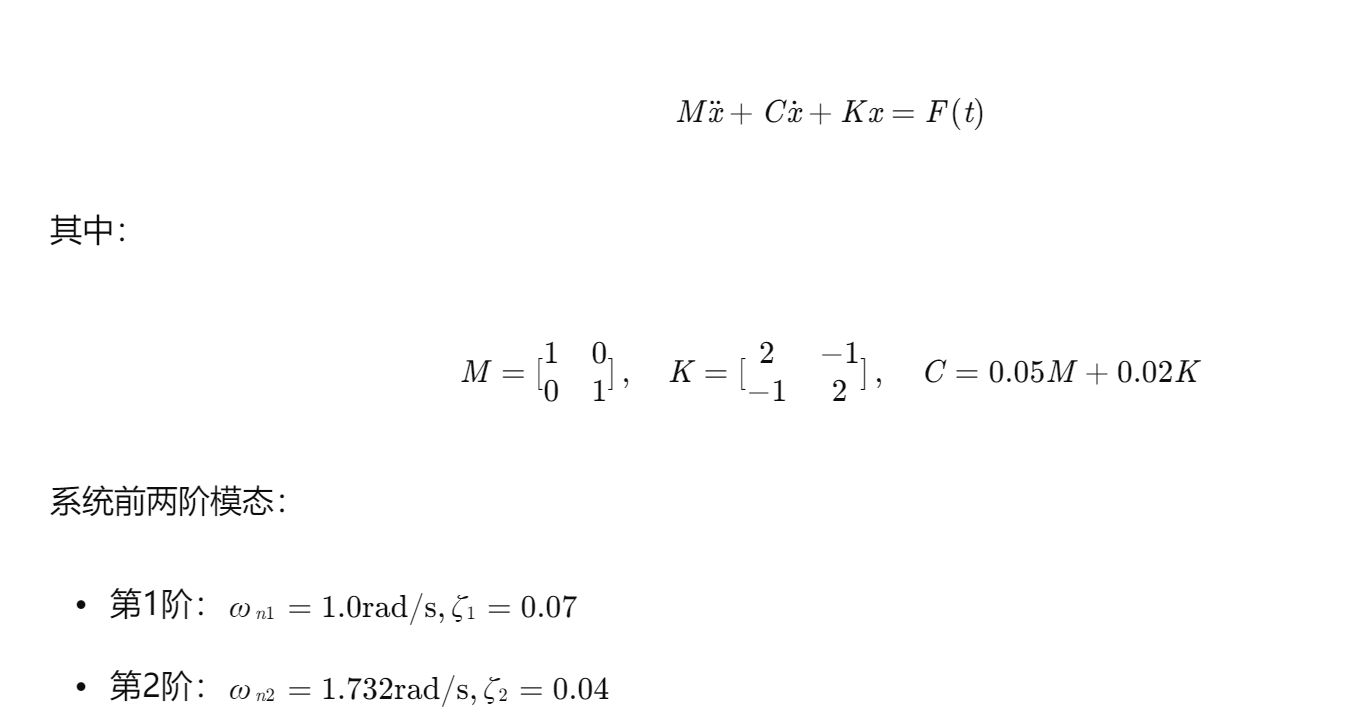
4.2 仿真设置

• 采样频率：fs=50Hz
• 数据长度：N=4096点
• 噪声水平：测量噪声标准差为0.01
• Hankel矩阵参数：ncols=2800,nrows=60,cut=4

4.3 结果分析

表1给出了模态参数估计结果对比：

模态	真实频率(rad/s)	估计频率(rad/s)	真实阻尼	估计阻尼
1	1.000	0.998	0.070	0.072
2	1.732	1.729	0.040	0.041

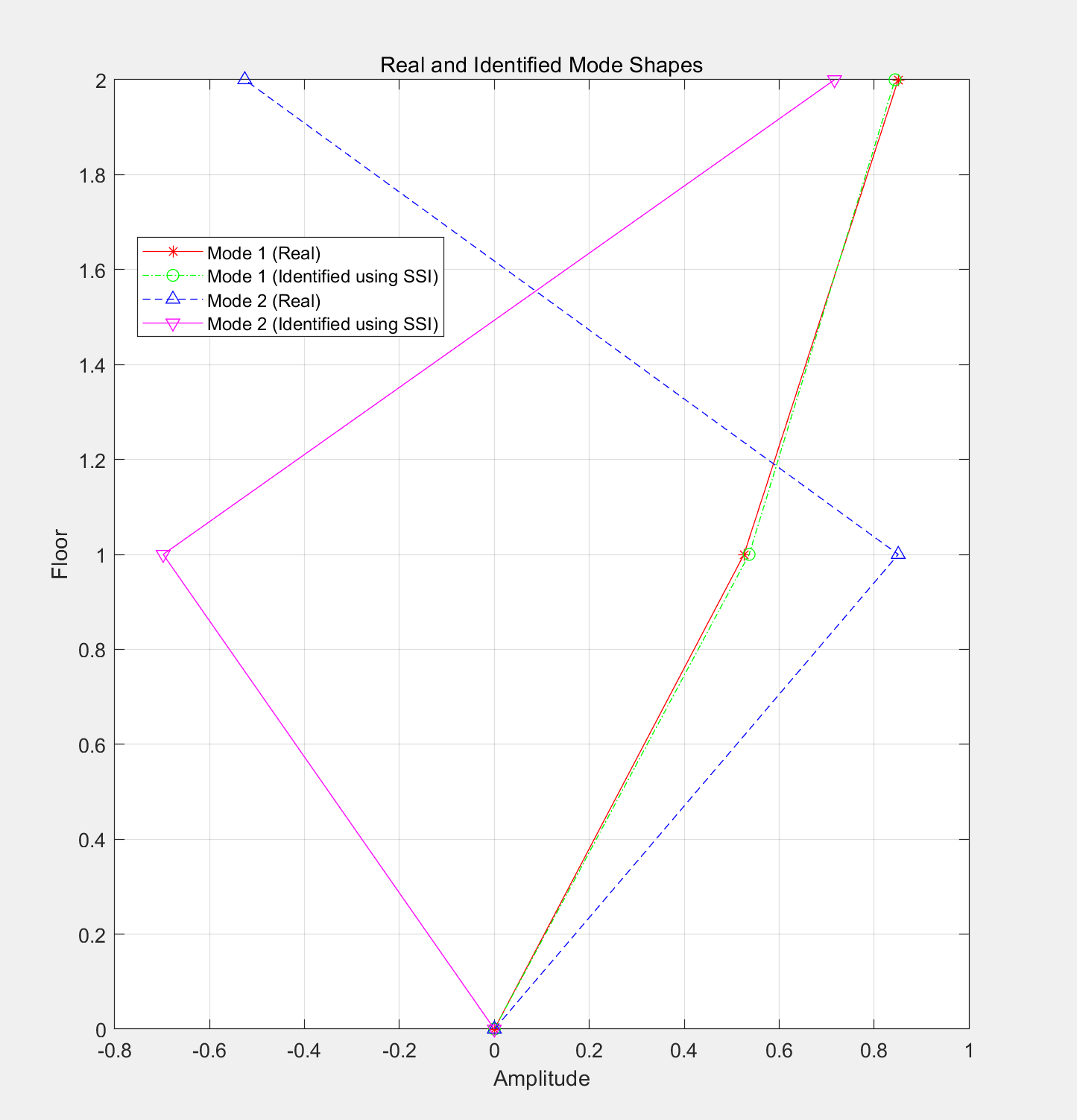
图1显示了CMI指标随模态阶数的变化，前两阶CMI值明显高于其他阶次，验证了模态估计的有效性。参与因子分析表明（图2），各质量块对两阶模态的贡献比例与理论分析一致。

5 结论

本文提出的随机子空间辨识方法能有效估计系统模态参数，计算的一致模态指标和参与因子为模态验证提供了可靠依据。数值仿真表明，该方法对含噪声的2自由度系统具有良好辨识精度，特别适用于输出-only模态分析场景。未来研究将扩展至大规模复杂结构并考虑非线性因素影响。

📚第二部分——运行结果

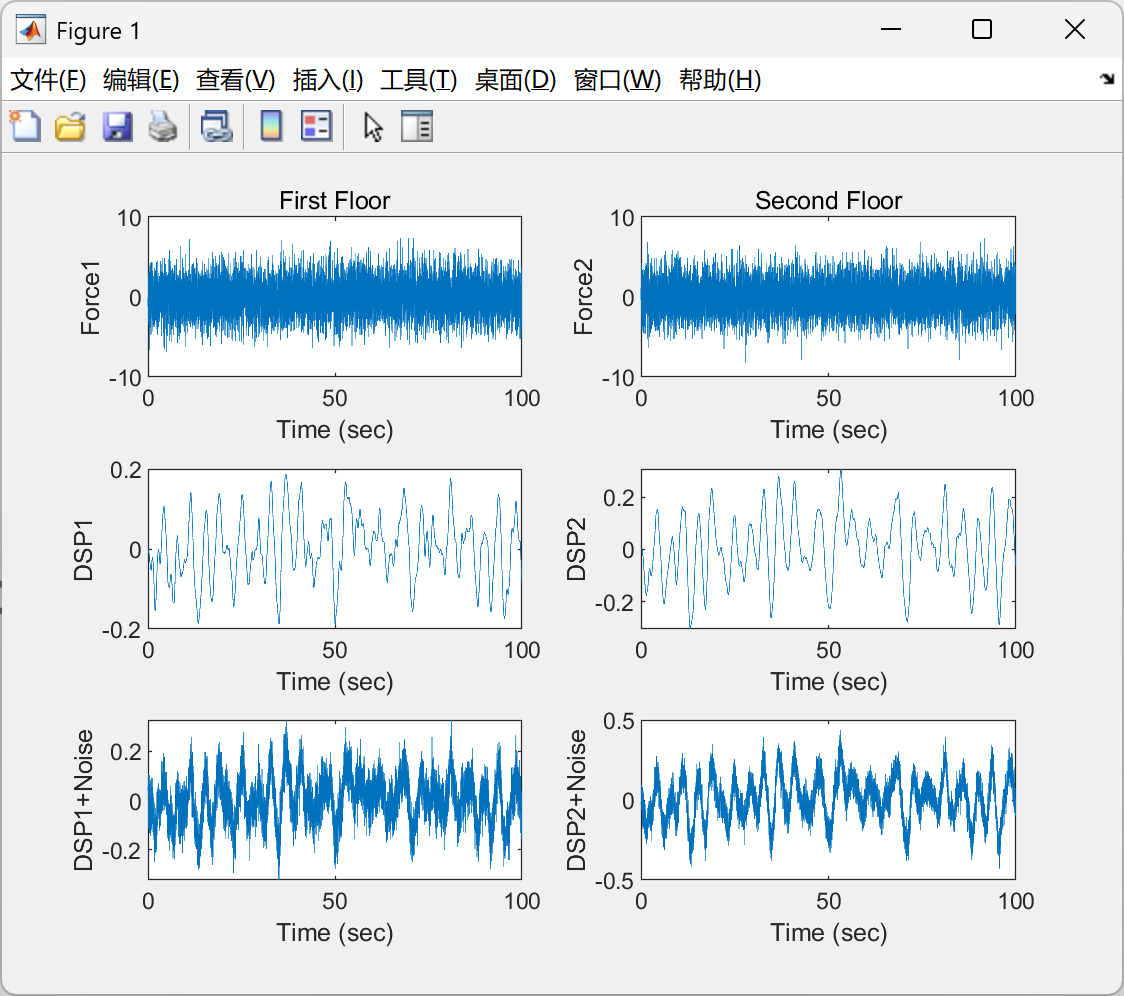
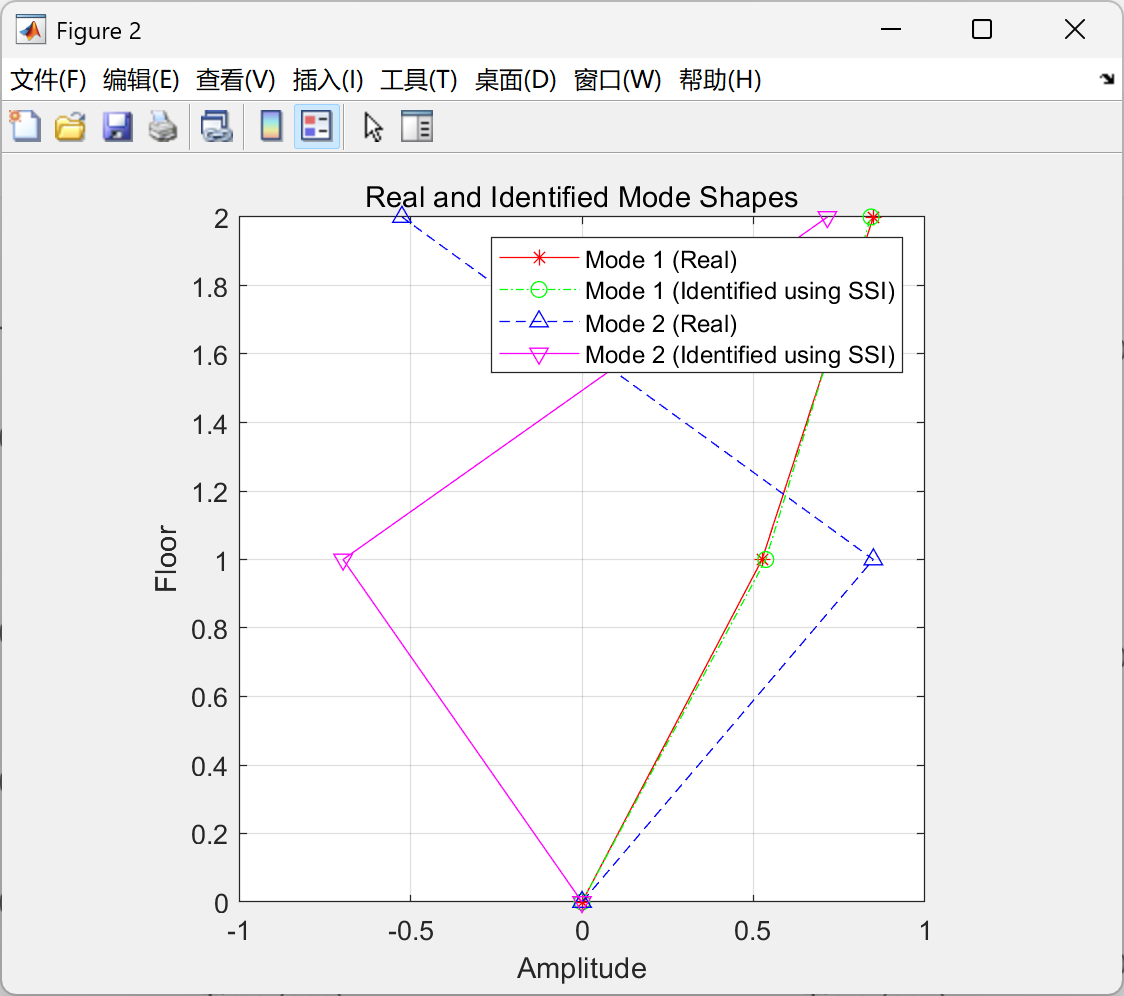
部分代码：

[outputs,npts]=size(output); % Computes the size of matrix output

if outputs > npts % Check if output matrix size is proper or should be transposed

output=output';

[outputs,npts]=size(output);

end

%--------------------------------------------------------------------------

% Find block sizes

brows=fix(nrows/outputs); % brows = how many output blocks.

nrows=outputs*brows; % Redefine the row numbers.

bcols=fix(ncols/1); % bcols = how many time steps.

ncols=1*bcols; % Redefine the column numbers.

m=1; % inputs number.

q=outputs; % outputs number.

%--------------------------------------------------------------------------

% Form the Hankel matriices Yp,Yf.

Yp=zeros(nrows/2,ncols); %Past Output

Yf=zeros(nrows/2,ncols); %Future Output

for ii=1:brows/2

for jj=1:bcols

Yp([(ii-1)*q+1:ii*q] ,[(jj-1)*m+1:jj*m] )=output(:,((jj-1)+ii-1)*m+1:((jj)+ii-1)*m);

end

end

for ii=brows/2+1:brows

i=ii-brows/2;

for jj=1:bcols

Yf([(i-1)*q+1:i*q] ,[(jj-1)*m+1:jj*m] )=output(:,((jj-1)+ii-1)*m+1:((jj)+ii-1)*m);

end

end

%--------------------------------------------------------------------------

% Projection

O=Yf*Yp'*pinv(Yp*Yp')*Yp;

🎉第三部分——参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈第四部分——本文完整资源下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python|数据|文档等完整资源获取