高等数学笔记-苏德矿-第十章-曲线积分和曲面积分-第七节-高斯公式与斯托克斯公式

本文链接：https://blog.youkuaiyun.com/Ding_Yifan/article/details/124943810

这篇笔记详细介绍了高等数学中的曲线积分和曲面积分，涵盖了高斯公式和斯托克斯公式的基本概念、散度和旋度的意义，以及第二类曲面积分的计算方法。高斯公式将曲面积分转化为三重积分，揭示了散度与流体源、汇的关系。斯托克斯公式则连接了曲线积分和曲面积分，说明了旋度与边界曲线积分的关系。此外，还讨论了空间曲线积分的类型和与路径无关的条件。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

高等数学笔记-苏德矿

第十章曲线积分和曲面积分

第七节高斯公式与斯托克斯公式

一、基本概念

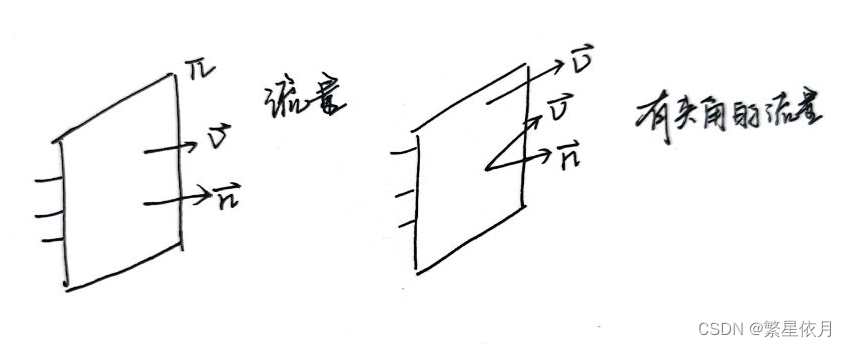
01 右手法则

伸出右手，使四指与边界曲线 $L$ 的方向一致，如果此时

大拇指的方向恰好与曲面 $Σ\Sigma$ 的法方向一致，称它们是符合右手法则的。

在这里插入图片描述

02 线单连通区域

设 $Ω⊂R3\Omega\subset R^3$ 是一个空间立体，对于 $Ω\Omega$ 中任意封闭曲线 $L$ ，不越过立体 $Ω\Omega$ 的边界曲面连续，

收缩为 $Ω\Omega$ 中的一点，称 $Ω\Omega$ 为线单连通区域。

03 面单连通区域

设 $Ω⊂R3\Omega\subset R^3$ 是一个空间立体，对于 $Ω\Omega$ 中任意封闭曲面 $Σ\Sigma$ ，不越过立体 $Ω\Omega$ 的边界曲面连续，

收缩为 $Ω\Omega$ 中的一点，称 $Ω\Omega$ 为面单连通区域。

比如厚球壳形状的立体是线单连通区域，不是面单连通区域。

二、高斯公式

设有界闭区域立体 $Ω⊂R3\Omega\subset R^3$ 的边界曲面是分片光滑曲线 $Σ\Sigma$ 指向外侧，若 $RP\ , \ Q\ , \ R$ 在 $Ω\Omega$ ( 包括 $Σ\Sigma$ ) 上连续且具有连续的一阶偏导数，则
$\oiint\limits_{\Sigma_{外}}Pdydz+Qdzdx+Rdxdy=\iiint\limits_{\Omega}(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dV$
$A⃗(x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)}\vec{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\}$ ， $dS⃗={dydz,dzdx,dxdy}d\vec{S}=\{dydz,dzdx,dxdy\}$ 。

高斯公式可以写成： $∯Σ外A⃗⋅dS⃗=∭ΩdivA⃗dV\displaystyle{ \oiint\limits_{\Sigma_{外}}\vec{A}\cdot d\vec{S}=\iiint\limits_{\Omega}\mathrm{div}\vec{A}dV }%$ 。

三、散度与旋度

01 散度

(1) 散度的概念

记 $∂P∂x+∂Q∂y+∂R∂z=divA⃗\displaystyle{ \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\mathrm{div}\vec{A} }%$ ，称 $A⃗(x,y,z)\vec{A}(x,y,z)$ 在点 $(x, y, z)$ 处的散度。
$\mathrm{div}\vec{A}(x_0,y_0,z_0)=\frac{\partial P}{\partial x}\Big|_{(x_0,y_0,z_0)}+\frac{\partial Q}{\partial y}\Big|_{(x_0,y_0,z_0)}+\frac{\partial R}{\partial z}\Big|_{(x_0,y_0,z_0)} =\mathrm{div}\vec{A}\Big|_{(x_0,y_0,z_0)}$

(2) 散度的意义

$M0(x0,y0,z0)∈Ω\forall\ M_0(x_0,y_0,z_0)\in\Omega$ ，取一个小立体 $V$ ，使 $M0∈V⊂ΩM_0\in V\subset\Omega$ ， $V$ 的边界曲面为分片光滑曲面 $Σ1\Sigma_1$ ，

$M∗∈V\displaystyle{ \oiint\limits_{\Sigma_{外}}\vec{A}\cdot d\vec{S}=\iiint\limits_{\Omega}\mathrm{div}\vec{A}dV=\mathrm{div}\vec{A}|_{M^*}\cdot V\ ,\ M^*\in V }%$ ，等式变形得： $divA⃗∣M∗=∯Σ1外A⃗⋅dS⃗V\displaystyle{ \mathrm{div}\vec{A}|_{M^*}=\frac{\oiint\limits_{\Sigma_{1外}}\vec{A}\cdot d\vec{S}}{V} }%$ .

等式右侧，即 $∯Σ1外A⃗⋅dS⃗V\displaystyle{\frac{\oiint\limits_{\Sigma_{1外}}\vec{A}\cdot d\vec{S}}{V}}%$ 称为流量 $Q$ 对体积 $V$ 的平均变化率。

令 $V→M0V\rightarrow M_0$ ，则有 $M∗→M0M^*\rightarrow M_0$ ， $lim⁡V→M0divA⃗∣M∗=lim⁡V→M0∯Σ1外A⃗⋅dS⃗V\displaystyle{\lim\limits_{V\rightarrow M_0}\mathrm{div}\vec{A}|_{M^*}=\lim\limits_{V\rightarrow M_0}\frac{\oiint\limits_{\Sigma_{1外}}\vec{A}\cdot d\vec{S}}{V}}%$ ，两侧取极限，得：

$divA⃗∣M0=lim⁡V→M0∯Σ1外A⃗⋅dS⃗V\displaystyle{\mathrm{div}\vec{A}|_{M^0}=\lim\limits_{V\rightarrow M_0}\frac{\oiint\limits_{\Sigma_{1外}}\vec{A}\cdot d\vec{S}}{V}}%$ ，此时等式右边称为在 $M_0$ 处流量 $Q$ 对体积 $V$ 的变化率，即 $divA⃗∣M0\mathrm{div}\vec{A}|_{M^0}$ 。

当 $divA⃗∣M0>0\mathrm{div}\vec{A}|_{M^0}>0$ ，称 $M_0$ 为流体的源；当 $divA⃗∣M0<0\mathrm{div}\vec{A}|_{M^0}<0$ ，称 $M_0$ 为流体的汇；

当 $divA⃗∣M0=0\mathrm{div}\vec{A}|_{M^0}=0$ ，称 $M_0$ 既不源也无汇。

(3) 散度的线性运算法则

线性运算法则：若 $B⃗(x,y,z)\vec{A}(x,y,z)\ , \ \vec{B}(x,y,z)$ 的分量偏导数均存在， $β\alpha\ ,\ \beta$ 为常数，

则 $div(αA⃗+βB⃗)=αdivA⃗+βdivB⃗\mathrm{div}(\alpha\vec{A}+\beta\vec{B})=\alpha\mathrm{div}\vec{A}+\beta \mathrm{div}\vec{B}$ 。

02 旋度

(1) 旋度的概念

$∮LPdx+Qdy+Rdz=∬Σ(∂R∂y−∂Q∂z)dydz+(∂P∂z−∂R∂x)dzdx+(∂Q∂x−∂P∂y)dxdy\displaystyle{\oint_{L}Pdx+Qdy+Rdz=\iint_{\Sigma}(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dzdx+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy}%$

曲面 $Σ\Sigma$ 的方向与边界曲线 $L$ 的方向符合右手系。

$A⃗(x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)}\vec{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\}$ ，

$ds⃗={dx,dy,dz}d\vec{s}=\{dx,dy,dz\}$ ， $dS⃗={dydz,dzdx,dxdy}d\vec{S}=\{dydz,dzdx,dxdy\}$ 。

${∂R∂y−∂Q∂z,∂P∂z−∂R∂x,∂Q∂x−∂P∂y}=△rotA⃗\displaystyle{\left\{\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right\}\stackrel{\triangle}{=}rot\vec{A}}%$ ，称 $A⃗(x,y,z)\vec{A}(x,y,z)$ 在点 $M (x, y, z)$ 处的旋度。
$rot\vec{A}\Big|_{(x_0,y_0,z_0)}=\left\{ (\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})\Big|_{(x_0,y_0,z_0)}+ (\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})\Big|_{(x_0,y_0,z_0)}+ (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})\Big|_{(x_0,y_0,z_0)} \right\}$

(3) 旋度的线性运算法则

线性运算法则：若 $B⃗(x,y,z)\vec{A}(x,y,z)\ , \ \vec{B}(x,y,z)$ 的分量偏导数均存在， $β\alpha\ ,\ \beta$ 为常数，

则 $rot(αA⃗+βB⃗)=αrotA⃗+βrotB⃗\mathrm{rot}(\alpha\vec{A}+\beta\vec{B})=\alpha\mathrm{rot}\vec{A}+\beta \mathrm{rot}\vec{B}$ 。

四、第二类曲面积分的类型

(1) $∯Σ外P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy\oiint\limits_{\Sigma_{外}}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy$

① 能用高斯公式就用高斯公式，化成三重积分容易计算。

② $Σ\Sigma$ 包围的内部有洞（ $P$ 或 $Q$ 或 $R$ 在洞上没有定义，称为”洞“ ）

如果在洞的外部 $RP\ , \ Q\ , \ R$ 偏导数均连续且 $divA⃗≡0\mathrm{div}\vec{A}\equiv0$ ，则

$∯Σ外Pdydz+Qdzdx+Rdxdy=∯Σ1外Pdydz+Qdzdx+Rdxdy\oiint\limits_{\Sigma_{外}}Pdydz+Qdzdx+Rdxdy=\oiint\limits_{\Sigma_{1外}}Pdydz+Qdzdx+Rdxdy$ .

( 注意， $Σ1\Sigma\ , \ \Sigma_1$ 包围同一些”洞“，且同侧。)

$Σ1\Sigma_1$ 的选择：

一般选择被积函数中分母表达式等于常数的封闭曲面 $Σ1\Sigma_1$ ，且 $Σ1\Sigma\ , \ \Sigma_1$ 包围同一些洞，同方向。

满足定理条件，化为 $Σ1\Sigma_1$ 上的第二类曲面积分，分母化简为常数，化简后 $RP\ , \ Q\ , \ R$ 偏导数处处连续，用高斯公式。

③ 直接计算，化成二重积分。

④ 化成第一类曲面积分计算，把 $cos⁡γ\cos\alpha\ , \ \cos\beta\ , \ \cos\gamma$ 求出来用 $x, y, z$ 表达式表示。

(2) $∬ΣPdydz+Qdzdx+Rdxdy\iint\limits_{\Sigma}Pdydz+Qdzdx+Rdxdy$

$∬ΣPdydz+Qdzdx+Rdxdy\iint\limits_{\Sigma}Pdydz+Qdzdx+Rdxdy$ ，其中 $Σ\Sigma$ 为非封闭曲面。

① 原式 $=∯Σ+Σ1−∬Σ1=\oiint_{\Sigma+\Sigma_1}-\iint_{\Sigma_1}$ ，其中 $Σ1\Sigma_1$ 为简单曲面，一般为平面块，前者用高斯公式，后者直接计算。

② 直接计算，化成二重积分容易计算。

③ 化成第一类曲面积分。

五、斯托克斯公式

若 $RP\ , \ Q\ , \ R$ 在分片光滑曲面 $Σ\Sigma$ ( 包括边界分段光滑曲线 $L$ ) 连续且具有连续的偏导数，

则 $∮LPdx+Qdy+Rdz=∬Σ(∂R∂y−∂Q∂z)dydz+(∂P∂z−∂R∂x)dzdx+(∂Q∂x−∂P∂y)dxdy\displaystyle{\oint_{L}Pdx+Qdy+Rdz=\iint_{\Sigma}(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dzdx+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy}%$

（ $=∣dydzdzdxdxdy∂∂x∂∂y∂∂zPQR∣=\displaystyle{ \left|\begin{array}{ll} dydz & dzdx & dxdy \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array}\right| }$ ，按第一行展开。）

曲面 $Σ\Sigma$ 的方向与边界曲线 $L$ 的方向符合右手法则。

注：以 $L$ 为边界的曲面 $Σ\Sigma$ 有无数个，选择简单的曲面，最好选择平面 $Σ\Sigma$ 。

引入旋度的概念后，斯托克斯公式也可写为： $∮LA⃗⋅ds⃗=rotA⃗⋅S⃗\displaystyle{ \oint_{L}\vec{A}\cdot d\vec{s}=\mathrm{rot}\vec{A}\cdot\vec{S} }%$ .

六、空间曲线积分与路径无关的条件

空间第二类曲线积分与路径无关的四个等价条件

设 $Ω\Omega$ 是空间的一个线单连通的一阶偏导数，则以下四个条件等价：

(1) 对 $Ω\Omega$ 中的任意封闭曲线 $L$ 上的第二类曲线积分为 $0$ ，即 $∮LPdx+Qdy+Rdz=0\oint_{L}Pdx+Qdy+Rdz=0$

(2) 对 $Ω\Omega$ 中的任意两个非封闭曲线 $ΓADB\Gamma_{ACB} \ , \ \Gamma_{ADB}$ ，

有 $∫ΓACBPdx+Qdy+Rdz=∫ΓADBPdx+Qdy+Rdz\displaystyle{ \int_{\Gamma_{ACB}}Pdx+Qdy+Rdz=\int_{\Gamma_{ADB}}Pdx+Qdy+Rdz }%$ ，

即 $Ω\Omega$ 中非封闭曲线上的第二类曲线积分只与起点和终点有关，与 $Ω\Omega$ 中的路径无关。

(3) 存在 $Ω\Omega$ 上的一个三元函数 $u (x, y, z)$ ，使 $d u = P d x + Q d y + R d z$ ，

即 $∂u∂z=R\displaystyle{ \frac{\partial u}{\partial x}=P\ , \ \frac{\partial u}{\partial y}=Q\ , \ \frac{\partial u}{\partial z}=R }%$ ，称 $u$ 是 $P d x + Q d y + R d z$ 的一个原函数。

(4) $∂P∂z≡∂R∂x\displaystyle{ \frac{\partial Q}{\partial x}\equiv\frac{\partial P}{\partial y}\ , \ \frac{\partial R}{\partial y}\equiv\frac{\partial Q}{\partial z}\ , \ \frac{\partial P}{\partial z}\equiv\frac{\partial R}{\partial x} }%$ ，即 $(x,y,z)∈Ω\mathrm{rot}\vec{A}\equiv0\ , \ (x,y,z)\in\Omega$ .

七、空间第二类曲线积分的类型

(1) $∮LPdx+Qdy+Rdz\oint_{L}Pdx+Qdy+Rdz$

① 能直接计算就直接计算，

$z=z(t)L:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases}$ ，找出起点对应的参数 $t_0$ ，找出终点对应的参数 $t_1$ 。化成参数的定积分。

② 斯托克斯公式。

(2) $∫ΓABPdx+Qdy+Rdz\int_{\Gamma_{AB}}Pdx+Qdy+Rdz$

① 能直接计算就直接计算，

$z=z(t)\Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases}$ 找出起点 $A$ 对应的参数 $t_A$ ，找出终点 $B$ 对应的参数 $t_B$ 。化成参数的定积分。

② 曲线积分的牛顿-莱布尼兹公式。

若找到 $u (x, y, z)$ ，使 $d u = P d x + Q d y + R d z$ ，

$∫ΓABPdx+Qdy+Rdz=∫A(x0,y0,z0)B(x1,y1,z1)du=u(x,y,z)∣A(x0,y0,z0)B(x1,y1,z1)\displaystyle{ \int_{\Gamma_{AB}}Pdx+Qdy+Rdz=\int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}du=u(x,y,z)\Big|_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)} }$

$∫A(x0,y0,z0)B(x1,y1,z1)Pdx+Qdy+Rdz=∫x0x1P(x,y0,z0)dx+∫y0y1Q(x1,y,z0)dy+∫z0z1R(x1,y1,z)dz\displaystyle{ \int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}Pdx+Qdy+Rdz=\int_{x_0}^{x_1}P(x,y_0,z_0)dx+\int_{y_0}^{y_1}Q(x_1,y,z_0)dy+\int_{z_0}^{z_1}R(x_1,y_1,z)dz }%$

③ 找到线单连通 $Ω\Omega$ 使 $ΓAB⊂Ω\Gamma_{AB}\subset\Omega$ ，有 $RP\ , \ Q\ , \ R$ 偏导数连续，且 $rotA⃗≡0\mathrm{rot}\vec{A}\equiv0$ ，知与路径无关。

$∫A(x0,y0,z0)B(x1,y1,z1)P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz\displaystyle{ \int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz }%$

$=∫x0x1P(x,y0,z0)dx+∫y0y1Q(x1,y,z0)dy+∫z0z1R(x1,y1,z)dz\displaystyle{ =\int_{x_0}^{x_1}P(x,y_0,z_0)dx+\int_{y_0}^{y_1}Q(x_1,y,z_0)dy+\int_{z_0}^{z_1}R(x_1,y_1,z)dz }%$

将 $x_1$ 换成 $x$ ，同理有：

$u(x,y,z)=∫A(x0,y0,z0)B(x1,y1,z1)Pdx+Qdy+Rdz+C\displaystyle{ u(x,y,z)=\int_{A(x_0,y_0,z_0)}^{B(x_1,y_1,z_1)}Pdx+Qdy+Rdz+C }%$ （与路径无关）

$=∫x0xP(x,y0,z0)dx+∫y0yQ(x,y,z0)dy+∫z0zR(x,y,z)dz+C\displaystyle{ =\int_{x_0}^{x}P(x,y_0,z_0)dx+\int_{y_0}^{y}Q(x,y,z_0)dy+\int_{z_0}^{z}R(x,y,z)dz+C }%$