高等数学笔记-苏德矿
第十章 曲线积分和曲面积分
第一节 第一类曲线积分
第一类曲线积分也称数量值函数的曲线积分。
一、第一类曲线积分的概念
问题:怎样求一段曲线弧状的质线的质量?
01 解决问题前的基本概念

02 由问题引入积分的定义
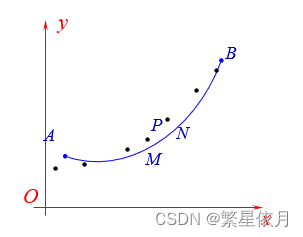
问题:若在曲线 ΓAB\Gamma_{AB}ΓAB 上点 PPP 的密度为 μ=f(P)\mu=f(P)μ=f(P) 连续,求 ΓAB\Gamma_{AB}ΓAB 的质量 MMM 。

(1) 分割:
相应地把曲线分成 nnn 个弧段 Mi−1Mi⌢\overset{\LARGE{\frown}}{M_{i-1}M_{i}}Mi−1Mi⌢,它的弧片记为 Δsi\Delta s_iΔsi,i=1,2,⋯ ,ni=1,2,\cdots,ni=1,2,⋯,n,λ=max1⩽i⩽nΔsi\lambda=\max \limits_{1 \leqslant i \leqslant n} \Delta s_{i}λ=1⩽i⩽nmaxΔsi 。
(2) 取近似:
∀ Pi∈Mi−1Mi⌢\forall\ P_i\in\overset{\LARGE{\frown}}{M_{i-1}M_{i}}∀ Pi∈Mi−1Mi⌢,ΔMi≈f(Pi)Δsi\Delta M_i\approx f(P_i)\Delta s_iΔMi≈f(Pi)Δsi,,i=1,2,⋯ ,ni=1,2,\cdots,ni=1,2,⋯,n 。
(3) 作和:
M=∑i=1nΔMi≈∑i=1nf(Pi)ΔsiM=\sum\limits_{i=1}^{n}\Delta M_i\approx\sum\limits_{i=1}^{n} f(P_i)\Delta s_iM=i=1∑nΔMi≈i=1∑nf(Pi)Δsi
(4) 取极限:
limλ→0∑i=1nf(Pi)ΔSi=M\lim \limits_{\lambda \rightarrow 0} \sum\limits_{i=1}^{n} f(P_i)\Delta S_i=Mλ→0limi=1∑nf(Pi)ΔSi=M
03 抽离物理背景的数学准备
去掉物理背景,取代密度 μ=f(P)\mu=f(P)μ=f(P) 为定义在曲线 ΓAB\Gamma_{AB}ΓAB 上的有界函数 f(P)f(P)f(P) 。
定义所加的条件本质上是保证该和式极限存在且唯一。
04 给出第一类曲线积分的定义
设 f(P)f(P)f(P) 在曲线 ΓAB\Gamma_{AB}ΓAB 上有定义且有界,若 limλ→0∑i=1nf(Pi)ΔSi\lim \limits_{\lambda \rightarrow 0} \sum\limits_{i=1}^{n} f(P_i)\Delta S_iλ→0limi=1∑nf(Pi)ΔSi 极限存在且唯一,
该极限值称为 f(P)f(P)f(P) 在曲线 ΓAB\Gamma_{AB}ΓAB 上的第一类曲线积分,又称数量值函数曲线积分。
记作 ∫ΓABf(P)ds\int_{\Gamma_{AB}}f(P)ds∫ΓABf(P)ds,即 ∫ΓABf(P)ds=limλ→0∑i=1nf(Pi)ΔSi\int_{\Gamma_{AB}}f(P)ds=\lim \limits_{\lambda \rightarrow 0} \sum\limits_{i=1}^{n} f(P_i)\Delta S_i∫ΓABf(P)ds=λ→0limi=1∑nf(Pi)ΔSi 。否则,称 f(P)f(P)f(P) 在曲线 ΓAB\Gamma_{AB}ΓAB 不可积。
极限存在且唯一的含义:
不论分点的插入方法或者 PiP_iPi 趋于哪一点,得到的和式极限值都存在,并且等于同一个值。
二、第一类曲线积分的定理和性质
01 第一类曲线积分的意义
(1) 几何意义

设 CCC 是 xyx yxy 平面上曲线,SSS 是以 CCC 为准线,母线垂直 xyx yxy 平面的柱面,
柱面高度为 f(x,y)f(x, y)f(x,y) ,求 xyx yxy 平面以上这部分柱面 SSS 的面积
结论:A=∫Cf(x,y)dsA=\int \limits_{C} f(x, y) d sA=C∫f(x,y)ds (曲线积分的几何意义)
(2) 物理意义
若 ∫ΓABf(P)ds\int_{\Gamma_{AB}}f(P)ds∫ΓABf(P)ds 存在且 f(P)⩾0f(P)\geqslant0f(P)⩾0,则 ∫ΓABf(P)ds\int_{\Gamma_{AB}}f(P)ds∫ΓABf(P)ds 表示密度 μ=f(P)\mu=f(P)μ=f(P) 曲线段 ΓAB\Gamma_{AB}ΓAB 的质量 MMM 。
02 第一类曲线积分的性质
第一类曲线具有二重积分的所有性质。
(1) 对 111 的积分等于该段弧长的长度:若 f(P)≡1f(P)\equiv1f(P)≡1,∫ΓAB1ds=∫ΓAB1ds=S\int _{\Gamma_{AB}}1ds=\int _{\Gamma_{AB}}1ds=S∫ΓAB1ds=∫ΓAB1ds=S
(2) 与曲线方向无关: ∫ΓABf(x,y)ds=∫ΓBAf(x,y)ds\displaystyle{ \int_{\Gamma_{AB}} f(x, y) d s=\int_{\Gamma_{BA}} f(x, y) d s }%∫ΓABf(x,y)ds=∫ΓBAf(x,y)ds
(3) 线性: ∫ΓAB[αf(x,y)+βg(x,y)]ds=α∫ΓABf(x,y)ds+β∫ΓABg(x,y)ds\displaystyle{ \int_{\Gamma_{AB}}[\alpha f(x, y)+\beta g(x, y)] d s=\alpha \int_{\Gamma_{AB}} f(x, y) d s+\beta \int_{\Gamma_{AB}} g(x, y) d s }%∫ΓAB[αf(x,y)+βg(x,y)]ds=α∫ΓABf(x,y)ds+β∫ΓABg(x,y)ds
(4) 可加性:设曲线段 ΓAC_{\Gamma_{AC}}ΓAC 与 ΓCB_{\Gamma_{CB}}ΓCB 首尾相接成曲线 ΓAB\Gamma_{AB}ΓAB
∫ΓABf(x,y)ds=∫ΓACf(x,y)ds+∫CBf(x,y)ds
\int _{\Gamma_{AB}}f(x, y) d s=\int_{\Gamma_{AC}} f(x, y) d s+\int_{CB} f(x, y) d s
∫ΓABf(x,y)ds=∫ΓACf(x,y)ds+∫CBf(x,y)ds
(5) 中值定理:设函数 fff 在光滑曲线段 CCC 上连续,则存在 (ξ,η)∈C(\xi, \eta) \in C(ξ,η)∈C,使得
∫Cf(x,y)ds=f(ξ,η)⋅sc(Sc为曲线段C的长度)
\int \limits_{C} f(x, y) d s=f(\xi, \eta) \cdot s_{c}\quad( S_{c} 为曲线段 C 的长度)
C∫f(x,y)ds=f(ξ,η)⋅sc(Sc为曲线段C的长度)
03 可积的必要条件
定理:若 f(P)f(P)f(P) 在光滑曲线 ΓAB\Gamma_{AB}ΓAB 上连续,则 f(P)f(P)f(P) 在 ΓAB\Gamma_{AB}ΓAB 可积,反之不成立。
三、第一类曲线积分的分类
01 平面第一类曲线积分
若 ΓAB⊂R2\Gamma_{AB}\subset\mathrm{R}^2ΓAB⊂R2,P(x,y)∈ΓABP(x,y)\in\Gamma_{AB}P(x,y)∈ΓAB,
∫ΓABf(P)ds=∫ΓABf(x,y)ds\int_{\Gamma_{AB}}f(P)ds=\int_{\Gamma_{AB}}f(x,y)ds∫ΓABf(P)ds=∫ΓABf(x,y)ds 称为平面第一类曲线积分。
02 空间第一类曲线积分
若 ΓAB⊂R3\Gamma_{AB}\subset\mathrm{R}^3ΓAB⊂R3,P(x,y,z)∈ΓABP(x,y,z)\in\Gamma_{AB}P(x,y,z)∈ΓAB,
∫ΓABf(P)ds=∫ΓABf(x,y,z)ds\int_{\Gamma_{AB}}f(P)ds=\int_{\Gamma_{AB}}f(x,y,z)ds∫ΓABf(P)ds=∫ΓABf(x,y,z)ds 称为空间第一类曲线积分。
第一类曲线积分可以求平面和空间的曲线弧长。
四、第一类曲线积分的计算
01 数量值函数曲线积分的计算
参数方程可以表示曲线方程更一般的形式。
设 ΓAB⊂R2\Gamma_{AB}\subset\mathrm{R}^2ΓAB⊂R2,且 ΓAB:{ x=x(t) y=y(t)α⩽t⩽β\Gamma_{AB}: \begin{cases}\ x=x(t) \\ \ y=y(t)\end{cases}\quad\alpha\leqslant t\leqslant\betaΓAB:{ x=x(t) y=y(t)α⩽t⩽β (微元法)
计算 ∫ΓABf(x,y)ds\int_{\Gamma_{AB}}f(x,y)ds∫ΓABf(x,y)ds .
设 Q=∫ΓABf(x,y)dsQ=\int_{\Gamma_{AB}}f(x,y)dsQ=∫ΓABf(x,y)ds ⇔\Leftrightarrow⇔ dQ=f(x,y)ds,(x,y)∈ΓABdQ=f(x,y)ds,(x,y)\in\Gamma_{AB}dQ=f(x,y)ds,(x,y)∈ΓAB
利用定积分中曲线弧长的微分公式 ds=x′2(t)+y′2(t) dtds=\sqrt{x'^2(t)+y'^2(t)}\ dtds=x′2(t)+y′2(t) dt .
要求 x′(t),y′(t)x'(t),y'(t)x′(t),y′(t) 连续不同时为0(光滑曲线)
从而 dQ=f(x(t),y(t))x′2(t)+y′2(t) dt , t∈[α,β]dQ=f(x(t),y(t))\sqrt{x'^2(t)+y'^2(t)}\ dt\ , \ t\in[\alpha,\beta]dQ=f(x(t),y(t))x′2(t)+y′2(t) dt , t∈[α,β] 。
所以,Q=∫ΓABf(x,y)dsQ=\int_{\Gamma_{AB}}f(x,y)dsQ=∫ΓABf(x,y)ds,且积分中 dsd sds 是弧长,取正值,故右端积分限应 α⩽β\alpha \leqslant \betaα⩽β 。
Q=∫ΓABf(x,y)ds=Q=∫αβf(x(t),y(t))x′2(t)+y′2(t)dt
Q=\int_{\Gamma_{AB}}f(x,y)ds=Q=\int_{\alpha}^{\beta}f(x(t),y(t))\sqrt{x'^2(t)+y'^2(t)}dt
Q=∫ΓABf(x,y)ds=Q=∫αβf(x(t),y(t))x′2(t)+y′2(t)dt
02 几种第一类曲线积分的计算
(1) 几种第一类平面曲线积分
① ΓAB:y=φ(x),x∈[a,b]\Gamma_{AB}:y=\varphi(x),x\in[a,b]ΓAB:y=φ(x),x∈[a,b] (x=x) 特殊的参数方程
φ’(x)\varphi’(x)φ’(x) 连续(以后默认)
∫ΓABf(x,y)ds=∫abf(x,φ(x))1+φ′2(x) dx
\int_{\Gamma_{AB}}f(x,y)ds=\int_{a}^{b}f(x,\varphi(x))\sqrt{1+\varphi'^2(x)}\ dx
∫ΓABf(x,y)ds=∫abf(x,φ(x))1+φ′2(x) dx
② ΓAB:x=ψ(y) , y∈[c,d] , ψ’(x)\Gamma_{AB}:x=\psi(y)\ , \ y\in[c,d]\ , \ \psi’(x)ΓAB:x=ψ(y) , y∈[c,d] , ψ’(x) 连续 ( y=yy=yy=y ) 特殊的参数方程
∫ΓABf(x,y)ds=∫cdf(ψ(y),y)1+ψ′2(y) dy
\int_{\Gamma_{AB}}f(x,y)ds=\int_{c}^{d}f(\psi(y),y)\sqrt{1+\psi'^2(y)}\ dy
∫ΓABf(x,y)ds=∫cdf(ψ(y),y)1+ψ′2(y) dy
③ ΓAB:r=r(θ) , θ∈[α,β] , r′(θ)\Gamma_{AB}:r=r(\theta)\ , \ \theta\in[\alpha,\beta]\ , \ r'(\theta)ΓAB:r=r(θ) , θ∈[α,β] , r′(θ) 连续
⇒ { x=r(θ)cosθ y=r(θ)sinθθ∈[α,β]\Rightarrow\ \begin{cases}\ x=r(\theta)\cos\theta \\ \ y=r(\theta)\sin\theta\end{cases}\quad\theta\in[\alpha,\beta]⇒ { x=r(θ)cosθ y=r(θ)sinθθ∈[α,β] ,x′2(θ)+y′2(θ)=r2(θ)+r′2(θ)x'^2(\theta)+y'^2(\theta)=r^2(\theta)+r'^2(\theta)x′2(θ)+y′2(θ)=r2(θ)+r′2(θ) . 强行构造参数方程
∫ΓABf(x,y)ds=∫αβf(r(θ)cosθ,r(θ)sinθ)r2(θ)+r′2(θ) dθ
\int_{\Gamma_{AB}}f(x,y)ds=\int_{\alpha}^{\beta}f(r(\theta)\cos\theta,r(\theta)\sin\theta)\sqrt{r^2(\theta)+r'^2(\theta)}\ d\theta
∫ΓABf(x,y)ds=∫αβf(r(θ)cosθ,r(θ)sinθ)r2(θ)+r′2(θ) dθ
④ ΓAB:θ=θ(r) , r∈[a,b] , θ′(r)\Gamma_{AB}:\theta=\theta(r)\ , \ r\in[a,b]\ , \ \theta'(r)ΓAB:θ=θ(r) , r∈[a,b] , θ′(r) 连续
⇒ { x=rcosθ(r) y=rsinθ(r)r∈[a,b]\Rightarrow\ \begin{cases}\ x=r\cos\theta(r) \\ \ y=r\sin\theta(r)\end{cases}\quad r\in[a,b]⇒ { x=rcosθ(r) y=rsinθ(r)r∈[a,b]
不作统一形式的公式,具体题目具体分析
好的思路:转化为 r=r(θ)r=r(\theta)r=r(θ) 或者关于x,y的方程
(2) 第一类空间曲线积分
若 ΓAB: { x=x(t) y=y(t) z=z(t)t∈[α,β]\Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases}\quad t\in[\alpha,\beta]ΓAB: ⎩⎪⎨⎪⎧ x=x(t) y=y(t) z=z(t)t∈[α,β],则
∫ΓABf(x,y,z)ds=∫αβf(x(t),y(t),z(t))x′2(t)+y′2(t)+z′2(t) dt
\int_{\Gamma_{AB}}f(x,y,z)ds=\int_{\alpha}^{\beta}f(x(t),y(t),z(t))\sqrt{x'^2(t)+y'^2(t)+z'^2(t)}\ dt
∫ΓABf(x,y,z)ds=∫αβf(x(t),y(t),z(t))x′2(t)+y′2(t)+z′2(t) dt
重积分被积函数一般不能化简,因为它满足的是不等式,而曲线曲面积分经常可以化简,因为它满足的是等式。




 本文详细解析了第一类曲线积分的概念,包括如何通过分割、近似和取极限求解曲线弧的质量,以及其几何和物理意义。介绍了定理、性质和计算方法,涉及平面和空间曲线积分,重点讲解了参数方程在计算中的应用。
本文详细解析了第一类曲线积分的概念,包括如何通过分割、近似和取极限求解曲线弧的质量,以及其几何和物理意义。介绍了定理、性质和计算方法,涉及平面和空间曲线积分,重点讲解了参数方程在计算中的应用。
















 3202
3202

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








