《几何原本》命题I.28
同位角相等，两直线平行；同旁内角互补，两直线平行。
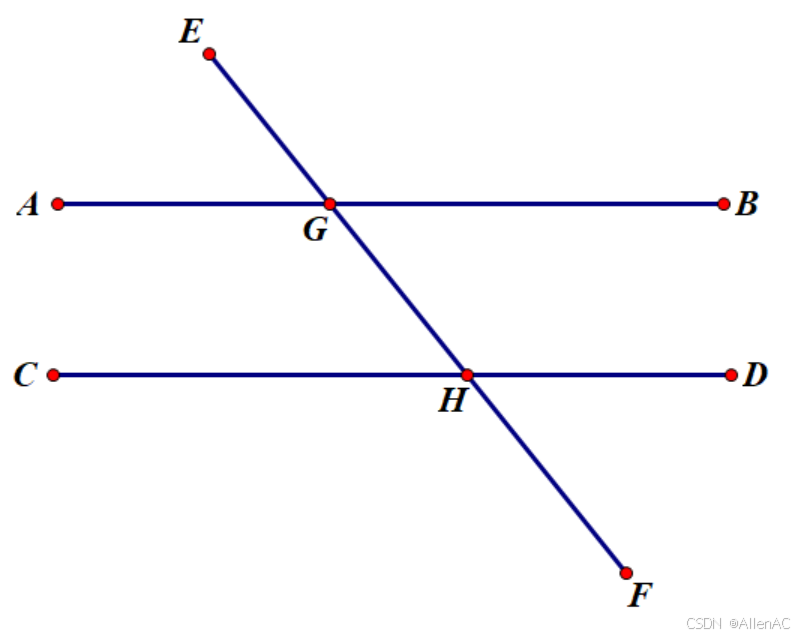
设 ∠EGB=∠GHD\angle EGB=\angle GHD∠EGB=∠GHD
∠EGB=∠AGH=∠GHD,AB∥CD\angle EGB=\angle AGH=\angle GHD,AB\parallel CD∠EGB=∠AGH=∠GHD,AB∥CD
设 ∠BGH+∠GHD=180∘\angle BGH+\angle GHD=180^{\circ}∠BGH+∠GHD=180∘
∠BGH=180∘−∠GHD=∠GHC,AB∥CD\angle BGH=180^{\circ}-\angle GHD=\angle GHC,AB\parallel CD∠BGH=180∘−∠GHD=∠GHC,AB∥CD
扫一扫
1408
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
