《几何原本》命题I.4
如果三角形的两条对应边及夹角相等，那么其第三边亦相等，两个三角形亦全等，其余的两对应角亦相等。
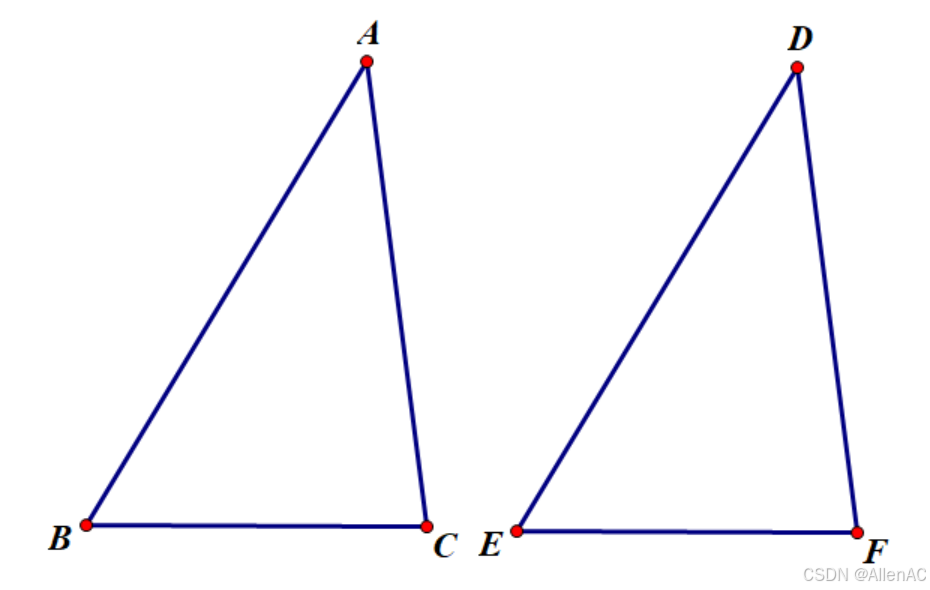
设 AB=DE,AC=DF,∠A=∠DAB=DE,AC=DF,\angle A=\angle DAB=DE,AC=DF,∠A=∠D
将 △ABC\triangle ABC△ABC 平移至 △DEF\triangle DEF△DEF 使得 AAA 与 DDD 重合、ABABAB 与 DEDEDE 重合
则 BBB 与 EEE 重合，CCC 与 FFF 重合、ACACAC 与 DFDFDF 重合
则 BC=EF,△ABC≅△DEF,∠B=∠E,∠C=∠FBC=EF,\triangle ABC \cong \triangle DEF,\angle B=\angle E,\angle C=\angle FBC=EF,△ABC≅△DEF,∠B=∠E,∠C=∠F
扫一扫
1406
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
