PCL Delaunay贪婪投影三角化（Surface_GreedyProjectionTriangulation）

PCL专栏目录及须知

用于无序点云的三角剖分，点云最好经过体素抽稀，保证点云平滑，且密度相差不大。

目录

1.Delaunay三角剖分

1.1 空圆性质

1.2 Delaunay三角剖分

1.2.1 概念

1.2.2 性质

1.2.3 算法流程

2. 使用场景

3. 关键函数

4.完整代码

5.结果展示

---

1.Delaunay三角剖分

1.1 空圆性质

即一个三角形（或边）的外接圆范围内（边界除外），不包含点集P中的任何顶点。

如下图：

黑色点为点集P。圆形为三角形的外接圆。图左，三角形的外接圆内部包含点集P中的其他顶点（不符合空圆性质）；图右，两个三角形外接圆的内部都不包含点集P中的其他顶点（符合空圆性质）；

1.2 Delaunay三角剖分

1.2.1 概念

所有三角形的外接圆均满足空圆性质的三角剖分，称为一个Delaunay三角剖分。

（1）Delaunay三角形：外接圆满足空圆性质的三角形。

（2）Delaunay边：外接圆满足空圆性质的三角形的其中一条边。

（3）局部Delaunay边：对三角剖分中的一条属于两个三角形的边e，若存在一个外接圆不包含三角形中的任何顶点称为局部Delaunay边。若一条边只属于一个三角形，也属于局部Delaunay边。Delaunay边一定是局部Delaunay的，但反过来未必。

（4）边翻转：对于点集的三角剖分并不唯一，例如下图：

图左图右是一个点集的不同三角剖分，两条红线代表不同的剖分方法。

如上面不唯一的剖分所示，从左边的竖着的那条红色的内对角线变成右边横着的内对角线的这个操作称作边翻转。每进行一次边翻转就会得到一个不同的剖分方案。

通过边翻转，实现不同的剖分方案，以得到满足空圆性质的Delaunay三角形。

1.2.2 性质

三角剖分得到的三角形，满足以下几个性质：

（1）空圆性

三角剖分后的所有三角面片都必须满足空圆性。

（2）最邻近性

任何一条连接于最邻近两点之间的边，都会创造出一个Delaunay三角形，也即必有一个外接圆满足该性质。

1.2.3 算法流程

（1）计算所有点云点的法向量。

（2）按照法向量方向，将点云投影到二维平面。

（3）从点云点集P中找到一个种子点pi，使用KD树进行邻域搜索，找到与种子点pi相邻的邻域点集C。

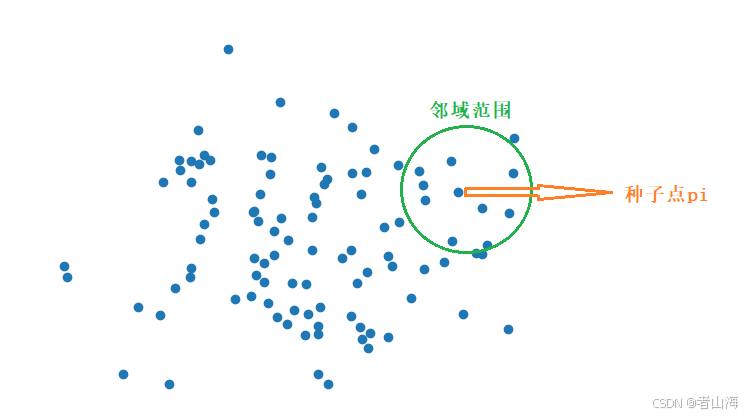
（4）连接投影后的（二维）种子点pi与投影后的（二维）种子点邻域点集C中的所有点，得到一个向量集合Cv。按照向量到x轴的角度排序向量集合Cv（绿色向量集合）。

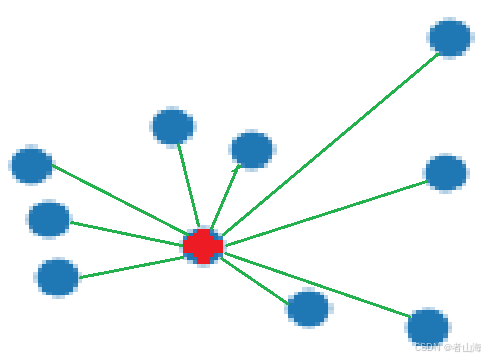
（5）按照排序依次连接pi和C中数据点，得到不交叠的三角形（可能存在重叠三角形）。

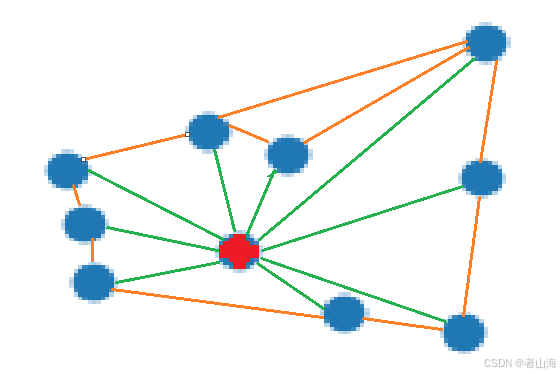
（6）删除重叠三角形

1）根据可见度删除重叠三角形：即删除被已有三角面片遮挡的数据点（图左三角形被遮挡，因此删除，得到图右）。

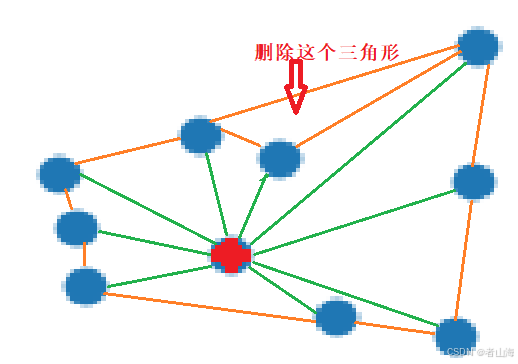
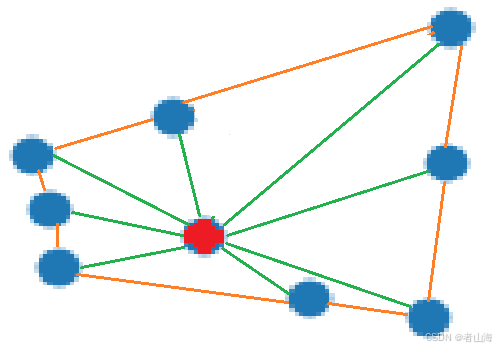
2）根据角度删除重叠三角形：

<1>按照pi到C中数据点的角度排列点集C中的数据。

<2>寻找最大角度，删除大角度中包含的小角度连接，得到三角面片。

（7）三角化

依次连接剩下的数据点，形成三角形。如果相邻数据点之间的角度过大（如大于150°），则不连接成为三角形，算法认为这是模型的孔洞。

（8）遍历所有点云，直到完成点云的三角剖分。

2. 使用场景

用于无序点云的三角剖分。

3. 关键函数

（1）邻域搜索半径，也就是三角形的最大边长

segmentation.setSearchRadius(0.15);

（2）种子点邻域搜索的最远距离，为了适应点云密度的变化

segmentation.setMu(2.5);

（3）种子点最多可搜索的邻域个数

segmentation.setMaximumNearestNeighbors(200);

（4）某点法线方向偏离样本点法线方向的最大角度（用于投影）

segmentation.setMaximumNearestNeighbors(200);

（5）三角化后得到三角形内角的最小角度（用于根据角度删除三角面）

segmentation.setMinimumAngle(M_PI / 18);

（6）三角化后得到三角形内角的最大角度（用于根据角度删除三角面）

segmentation.setMaximumAngle(2 * M_PI / 3);

（7）是否保证法线朝向一致（用于投影）

segmentation.setNormalConsistency(false);

4.完整代码

#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/io/ply_io.h>
#include <pcl/point_types.h>
#include <pcl/search/kdtree.h>
#include <pcl/features/normal_3d.h>
#include <pcl/surface/gp3.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <boost/thread/thread.hpp>

int main()
{
    /****************贪婪投影三角化********************/
    pcl::PointCloud<pcl::PointXYZRGB>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZRGB>);				// 源点云
    pcl::io::loadPCDFile("D:/code/csdn/data/bunny2.pcd", *cloud);

    // 计算法线
    pcl::NormalEstimation<pcl::PointXYZRGB, pcl::Normal> n;
    pcl::search::KdTree<pcl::PointXYZRGB>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZRGB>);
    n.setInputCloud(cloud);
    n.setSearchMethod(tree);
    n.setKSearch(20);                                                                                   // k邻域搜索范围
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    n.compute(*normals);

    pcl::PointCloud<pcl::PointXYZRGBNormal>::Ptr cloudNormals(new pcl::PointCloud<pcl::PointXYZRGBNormal>);         // 连接点云及法向量
    pcl::concatenateFields(*cloud, *normals, *cloudNormals);

    // 贪婪投影三角化
    pcl::GreedyProjectionTriangulation<pcl::PointXYZRGBNormal> segmentation;
    pcl::search::KdTree<pcl::PointXYZRGBNormal>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZRGBNormal>);
    segmentation.setInputCloud(cloudNormals);                                                                       // 输入点云（需包含法线）
    segmentation.setSearchMethod(tree2);
    segmentation.setSearchRadius(0.15);                                                                             // 邻域搜索半径，也就是三角形的最大边长
    segmentation.setMu(2.5);                                                                                        // 种子点邻域搜索的最远距离，为了适应点云密度的变化
    segmentation.setMaximumNearestNeighbors(200);                                                                   // 种子点最多可搜索的邻域个数
    segmentation.setMaximumSurfaceAngle(M_PI_4);                                                                    // 某点法线方向偏离样本点法线方向的最大角度
    segmentation.setMinimumAngle(M_PI / 18);                                                                        // 三角化后得到三角形内角的最小角度
    segmentation.setMaximumAngle(2 * M_PI / 3);                                                                     // 三角化后得到三角形内角的最大角度
    segmentation.setNormalConsistency(false);                                                                       // 是否保证法线朝向一致
    pcl::PolygonMesh triangles;                                                                                     // 存储最终三角化的网格模型
    segmentation.reconstruct(triangles);

    std::vector<int> parts = segmentation.getPartIDs();                                                             // 获取顶点信息
    std::vector<int> states = segmentation.getPointStates();

    pcl::io::savePLYFile("D:/code/csdn/data/bunny2.ply", triangles);

    /****************展示********************/
    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("GreedyProjectionTriangulation"));
    viewer->addPointCloud(cloud, "cloud");
    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer0(new pcl::visualization::PCLVisualizer("GreedyProjectionTriangulation1"));
    viewer0->addPolygonMesh(triangles, "triangles");
    viewer0->setRepresentationToWireframeForAllActors();          // 网格模型以线框图模式显示

    while (!viewer->wasStopped() || !viewer0->wasStopped())
    {
        viewer->spinOnce(100);
        viewer0->spinOnce(100);
        boost::this_thread::sleep(boost::posix_time::microseconds(100000));
    }

    return (0);
}

5.结果展示

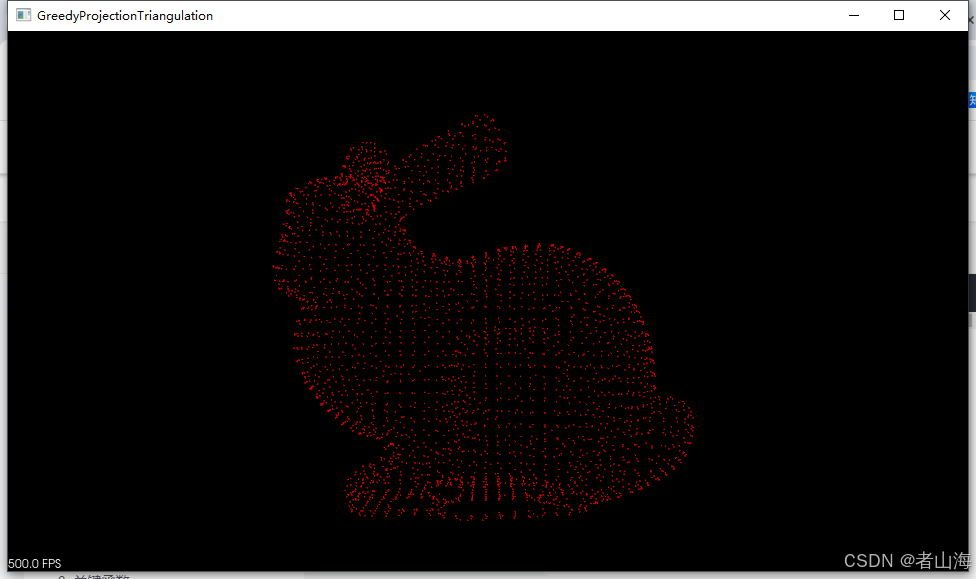
原始点云

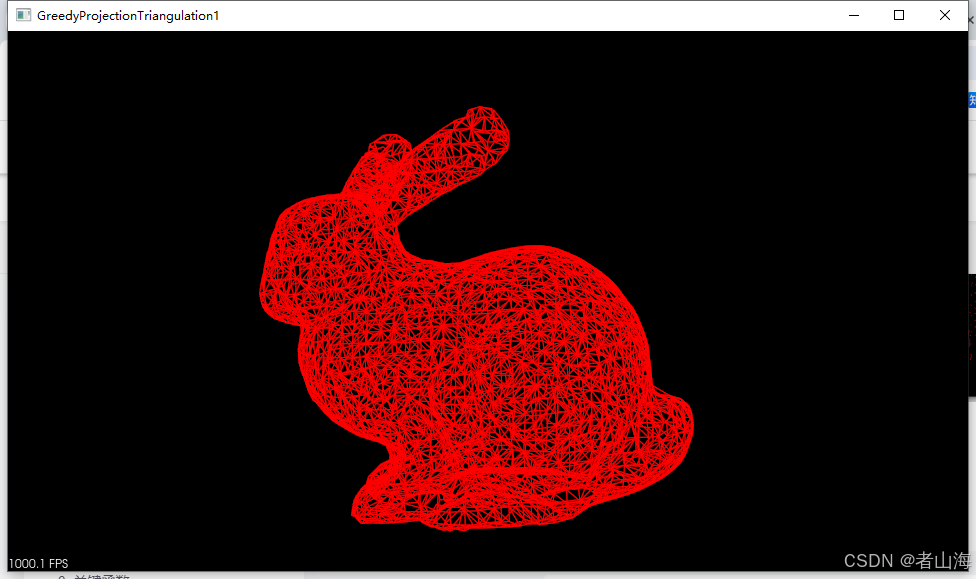
结果点云