基线方程的推导和基于双差载波观测方程的基线方程解算

 前言

        笔者水平有限，有错漏之处还望指出，不胜感激！

        参考视频：​​​​​​卫星导航定位原理与应用_中国大学MOOC(慕课)https://www.icourse163.org/learn/SEU-1449624174?tid=1473187448#/learn/content?type=detail&id=1260228084&cid=1296304241&contentid=1220032219卫星导航系统_中国大学MOOC(慕课)https://www.icourse163.org/learn/HRBEU-1207123826?tid=1473239462#/learn/content?type=detail&id=1260473592&cid=1296834056&contentid=480000001473950

基线方程的推导

                                                                                ​​​​​​​                ​​​​​​​        ​​​​​​​        ​​​​​​​        

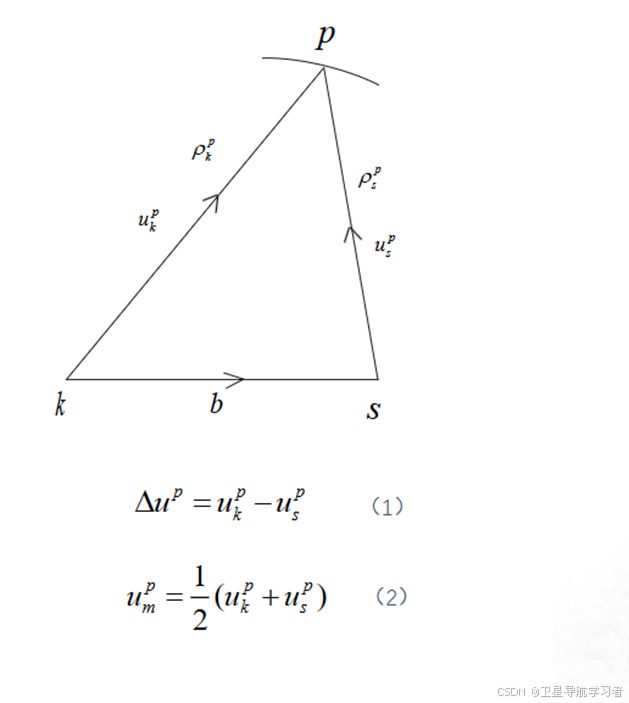
        如上图所示，两个测站k，s分别观测卫星p，为测站k至卫星p的星地距离，为测站k至卫星p的星地距离.

        做辅助线，使得右上角三角形为等腰三角形，如下图：

                                ​​​​​​​​​​​​​​        ​​​​​​​        ​​​​​​​     

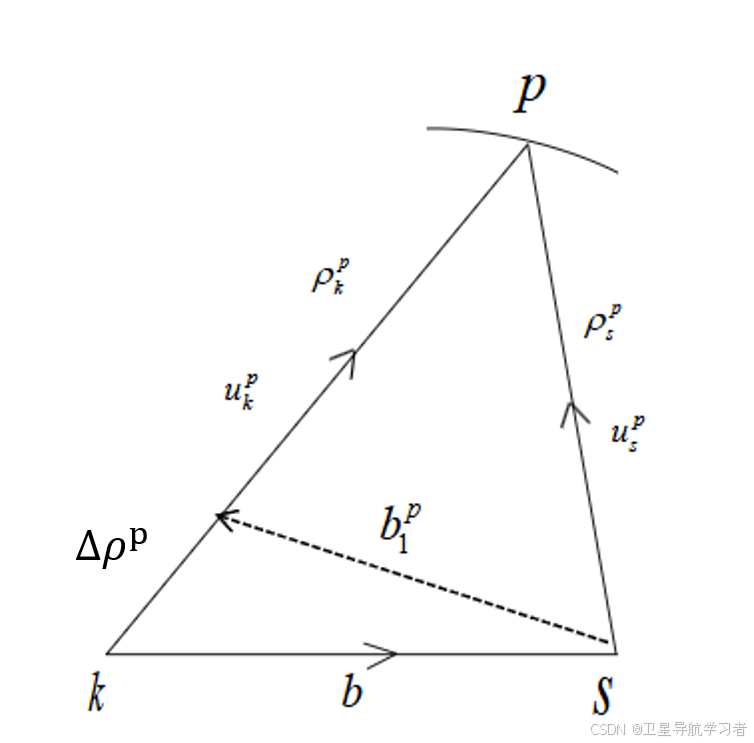
        因为为等腰三角形，所以：

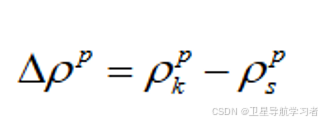                                                                                               （3）

        且：

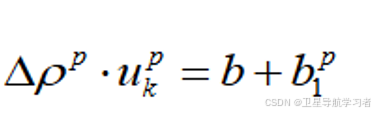        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                                （4）

        辅助线通过向量kp与sp相减可得:

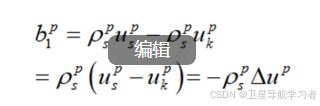  ​​​​​​​        ​​​​​​​        ​​​​​​​                                                 （5）

         将式（4）代入：        ​​​​​​​        ​​​​​​​    

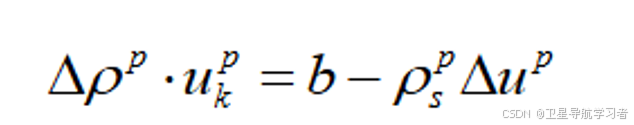                                                                       （6）

        将上式两端同×（也就是平均向量）：

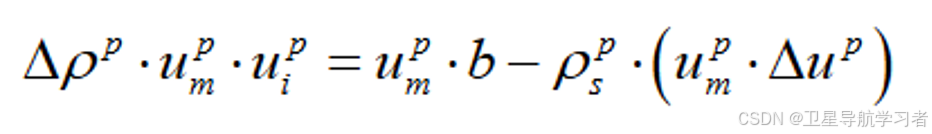        ​​​​​​​        ​​​​​​​           （7）  

        对上式进行化简，截取其中部分式子如下：

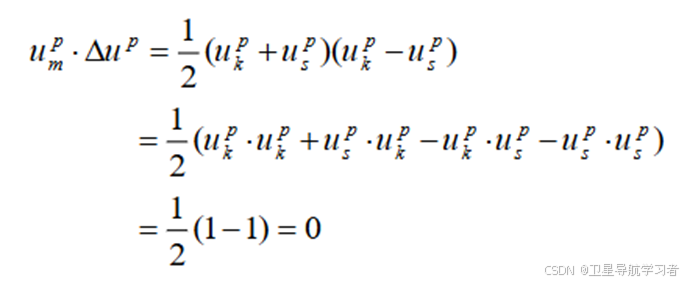                        ·                              （8）

        将上式代入式（7）中，得到：

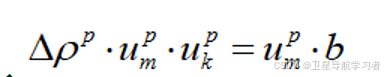        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                       （9）

        将表达式代入左侧，得到：

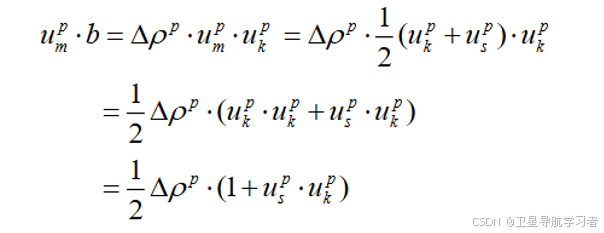        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​              (10)

        而，两向量点乘，我们引入顶角角度：

                                                        

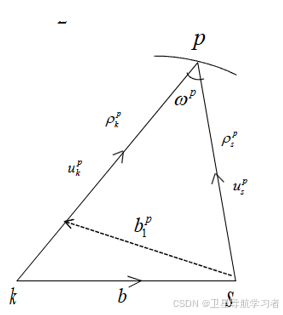
        根据向量点乘法则：

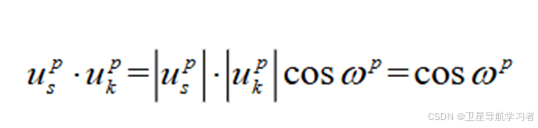        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                        （11）

        将式（11）代入式（10），可得：

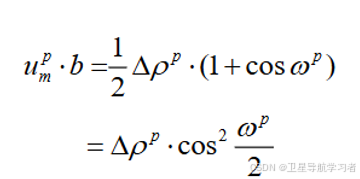                                                                              （12）

        对上式进行变形，可以得到：

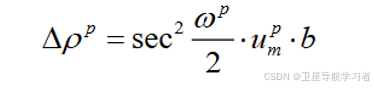                                                       （13）

        同理，对于卫星q，可以得到：

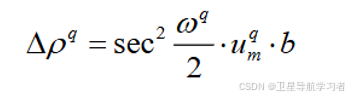        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​             （14）

        回顾双差载波方程：

                       （15）

        可以发现上述两项即为不同接收机对于卫星的星地距离差值，因此我们进行代入：        

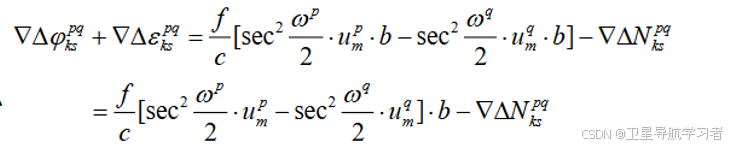           （16）

        当基线长度小于40km时，，因此：

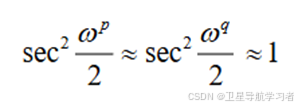        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                   （17）

        代入式（16）：

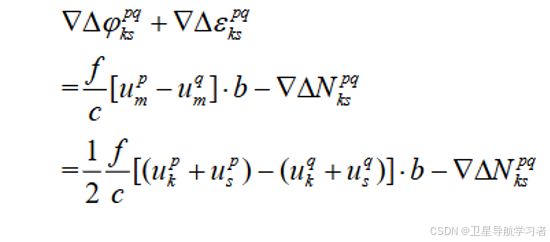                                     （18）

        将单位向量，等用卫星和接收机相对坐标增量，这里可以用测站近似坐标和卫星坐标进行表示即可，同时将距离b用两个接收机之间距离差表示：

                                       (19)

        将上式代入式（18），得出基线方程：

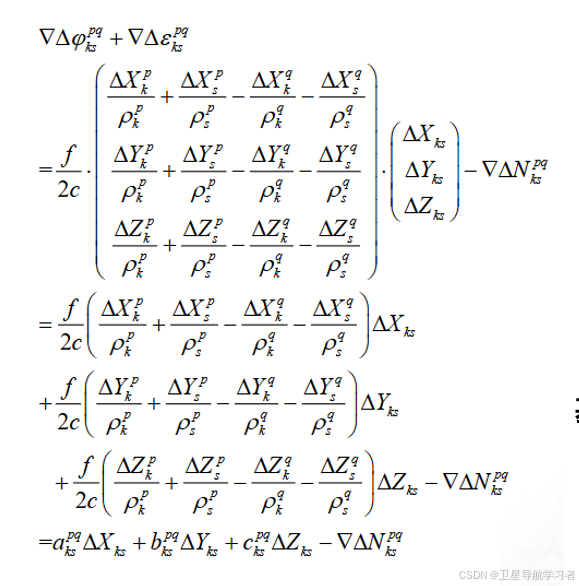                                                （20）

基线方程的解算：

        为了进行方程的解算，需要将其化为误差方程的形式，且其变量应为实际坐标差的变化值：     

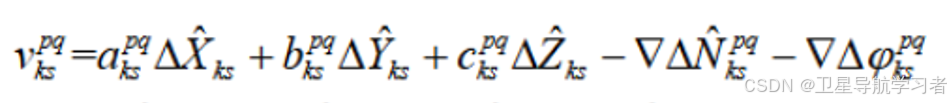           ​​​​​​​     （21）

        将上式化为变化值：   ​​​​​​​        ​​​​​​​    

        ​​​​​​​        ​​​​​​​                      （22）

        式中：

        ​​​​​​​        ​​​​​​​        ​​​​​​​                ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

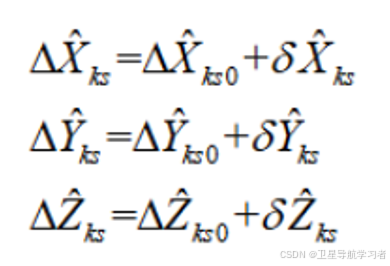
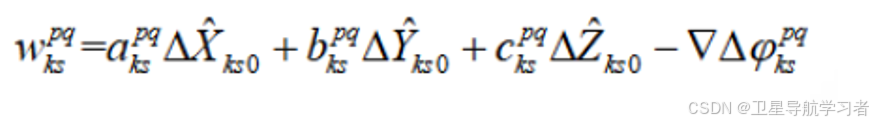
        不妨对式（22）进行观察，可以发现其含有4个未知数，分别为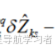：，，三个基线向量坐标增量，和一个双差模糊度。

        如果以某一个卫星作为参考卫星，某一历元在测站i和测站j上，同时观测了S个卫星，则可列出(S-1)个形如式（22）的误差方程，相应地要引入(S-1)个双差模糊度未知数，再考虑到有3个基线向量未知数，则该历元共有s+2个未知数，未知数个数大于方程数，此时，误差方程组不可解，
        若测站i和测站i对所有S个卫星进行连续观测，随着历元数的增加，误差方程数也在增加，但未知数没有变。假设观测了n个历元，则总共有n*(s-1)个误差方程方程数大于未知数个数，进而实现了误差方程组可解。

        对m个卫星进行多历元观测：

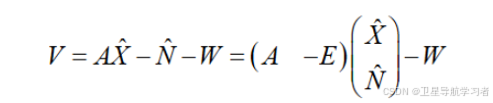        ​​​​​​​        ​​​​​​​        ​​​​​​​                          （23）     

        式中：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​             

        ​​​​​​​根据最小二乘法，已知观测值的方差矩阵D的条件下进行未知数的求解：

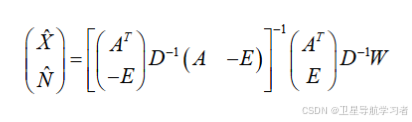        ​​​​​​​        ​​​​​​​        ​​​​​​​                     （24）