前言
最近正在学习卫星导航定位的基本原理,在进行组会汇报时发现纸上得来终觉浅,还是实际自己推导一下会印象更加深刻,因此准备记录一下学习心得,既是方便回顾,也能巩固知识,笔者水平有限,有错漏之处还望指出,不胜感激!
参考视频:卫星导航定位原理与应用_中国大学MOOC(慕课)![]() https://www.icourse163.org/learn/SEU-1449624174?tid=1473187448#/learn/content?type=detail&id=1260228084&cid=1296304241&contentid=1220032219卫星导航系统_中国大学MOOC(慕课)
https://www.icourse163.org/learn/SEU-1449624174?tid=1473187448#/learn/content?type=detail&id=1260228084&cid=1296304241&contentid=1220032219卫星导航系统_中国大学MOOC(慕课)![]() https://www.icourse163.org/learn/HRBEU-1207123826?tid=1473239462#/learn/content?type=detail&id=1260473592&cid=1296834056&contentid=480000001473950
https://www.icourse163.org/learn/HRBEU-1207123826?tid=1473239462#/learn/content?type=detail&id=1260473592&cid=1296834056&contentid=480000001473950
载波相对定位
1.1载波相位观测方程
当接收机来自卫星的信号后,接收机信号和卫星信号会有一个相位差。因为我们只能确定两者相位的小数部分F(t1),对于整数部分,也就是周,无法确定,这也是下图中整周模糊度N的概念。
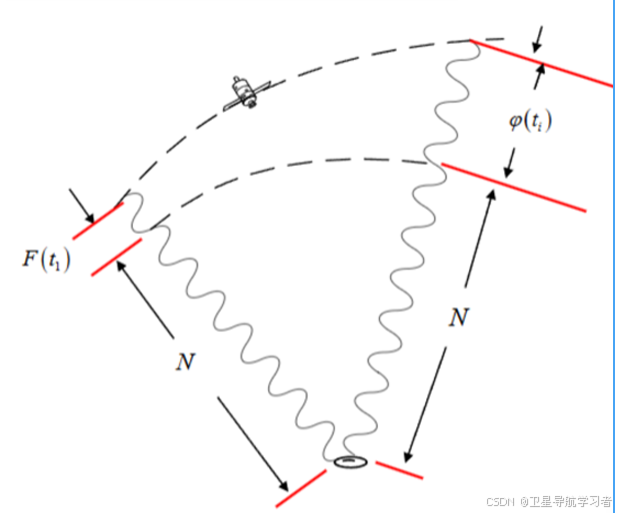
对于上图中相位差,我们可以采用一下形式进行表示:
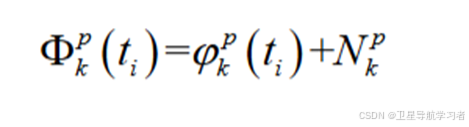
同时,我们也可以通过最基础的相位表示方法:载波频率乘以时间进行表示:
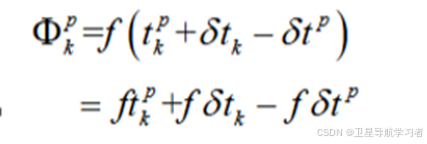
其中,为信号传递时间,
为接收机钟差,
为卫星钟差。
联立上述两式,得到:
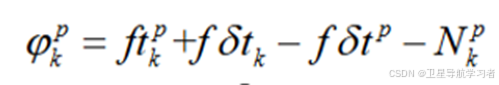
将转为星地距离表示,按照距离=速度✖时间,应该由平均速度乘以
表示,但其值较难测量,所以用光速c近似表示,但要因此引入对流层误差和电离层误差:
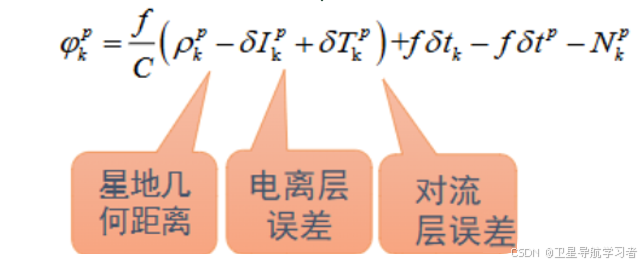
和伪距一样,相位观测值包含观测值和随机误差,引入随机误差,得到载波相位观测方程:
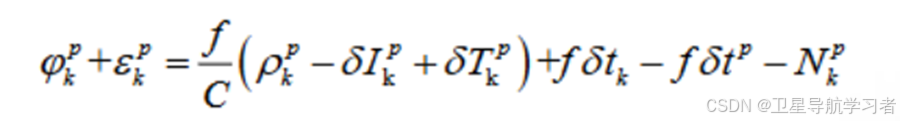
1.2载波相对定位
在前面,我们学习过伪距单点定位方法,单点定位也称为绝对定位。对于载波观测值来说,在理论上,我们也可以采用类似方法进行绝对定位。但是,由于各误差项的数学模型还不够完善,由模型所得的结果精度不高,这对于精度不高的伪距观测值来说可以忽略。但是,对于测量精度远远高于伪距的载波观测值来说,各误差项的模型误差就成为了影响高精度定位的主要因素。因此,需要寻找新的途径,消除各系统误差的影响,以实现快速、高精度定位。
假设有两台GNSS接收机,分别架设在k点和s点同步观测相同的GNSS卫星。当两站距离相隔不远的情况下,对于同一个卫星,电离层、对流层对两站GNSS观测值的影响可近似看做相等,使得定位结果向同一个方向偏移。在这种情况下,可以得到很高精度的两站间相对坐标。这种利用两台GNSS接收机,同步观测相同的卫星,利用载波观测值,得到两站间相对位置的定位方法,称作载波相对定位。
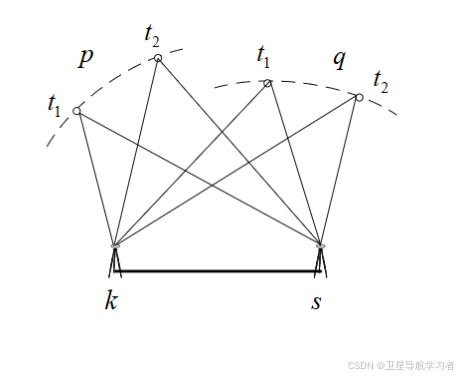
根据之前的载波相位观测方程,得到下列四组方程:
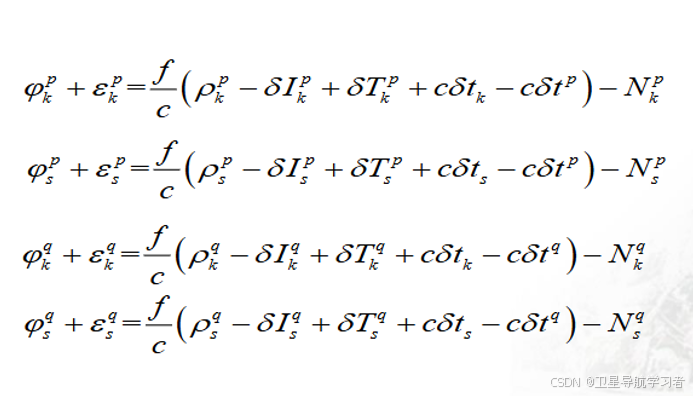
单差:
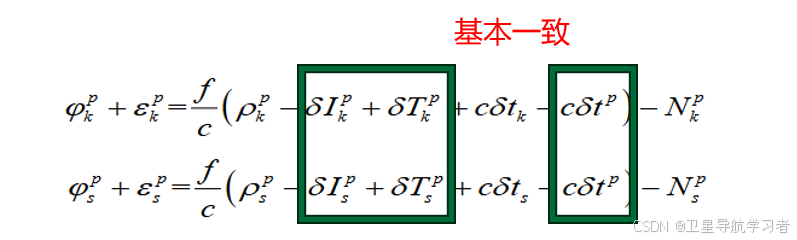
对于两个接收机同时接收一个卫星的载波相位观测方程进行做差,因为距离较近,所以电离层误差和对流层误差基本一致,同时卫星钟差也相等,因此可以得到单差载波观测方程:
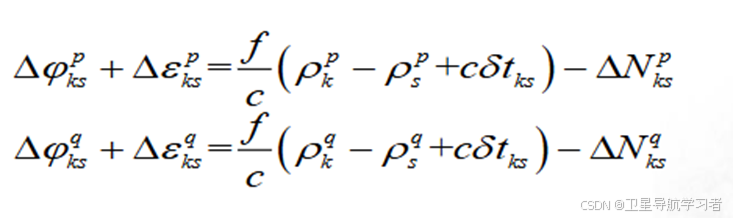
双差:
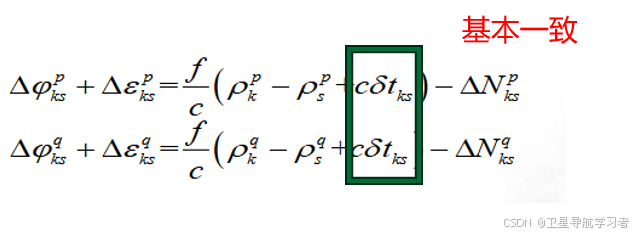
因为两个接收机的钟差之差是一致的,因此对于两个单差载波观测方程进行做差,可以得到双差载波观测方程如下:
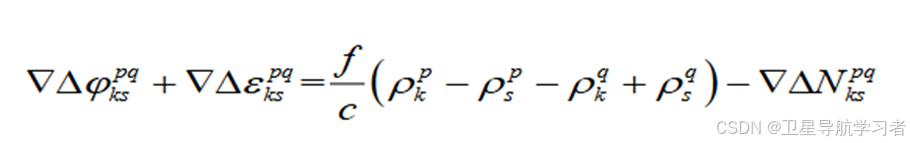
因为整周模糊度对于后续提升载波定位精度还有作用,可以利用其整数特性,因此在实际使用中经常使用双差载波观测方程。
三差:
如果还想进一步消去对应参数,可以对两个不同历元的双差载波观测方程进行做差,因为模糊度不会随着历元数进行变化,其在首次对该卫星进行观测时就已确定,因此不同历元的模糊度相同:
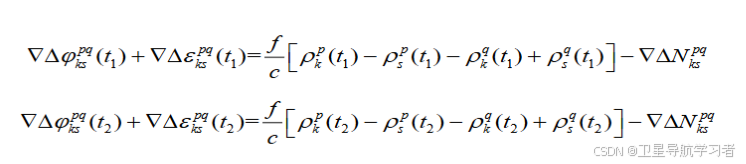
相减得到三差载波观测方程:
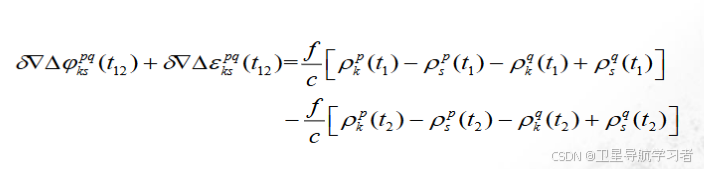
总结:
本章讲述了载波相位观测方程和相对定位方程的建立,但还是不能进行坐标的相对位置的求解,因为在载波相对定位中,求得的是两站相对坐标,也即基线向量。因此,如何将双差观测值表示成基线向量的函数,将在下一个博客进行讲解。
基线方程的推导和基于双差载波观测方程的基线方程解算-优快云博客![]() https://blog.youkuaiyun.com/weixin_61546541/article/details/143976485
https://blog.youkuaiyun.com/weixin_61546541/article/details/143976485





















 1361
1361

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










