规划算法很难？一篇教你掌握（附代码）

 概要

        规划模型中的“规划”是以目标为核心、以约束为边界、以数学建模为工具、以优化解为输出的系统性决策过程，“规划” 其实就是把实际问题变成一个 “数学 puzzle”的过程。打个比方：你想周末安排一天出去玩，目标是“玩得开心又花钱最少”，这就是你的“目标”；但你受限于“只有 8 小时时间”“最多带 500 块钱”“想去的地方之间有距离”，这些就是“约束”。

规划的类型

规划模型包括线性规划、非线性规划、整数规划。

归类算法如何判断？

总结：算法选择的“三步判断法”

（1）看变量类型：

1.连续变量→线性/非线性规划（再看函数是否线性）。

2.整数变量→整数规划（若仅0-1，则为零一规划）。

（2）看函数形态：

1.线性函数→线性规划/整数线性规划。

2.非线性函数→非线性规划/整数非线性规划。

（3）看问题规模：

1.小规模（变量<50）→优先精确算法（单纯形法、分支定界法）。

2.大规模（变量>100）→启发式算法（遗传算法、粒子群算法等）。

知识讲义

一、线性规划

（一）适用条件

函数形态和约束条件都是线性函数，决策变量为连续实数，解决中小规模问题。

（二）使用情景

情景①：资源分配的问题：用有限的原材料生产多种产品，最大化利润。

情景②：运输问题：从多个仓库向多个点运货，最小运输成本。

情景③：混合配料问题：按比例混合多种原材料，满足质量标准并且成本最低。

  （三）典型案例

情景①：资源分配问题

【简单】某工厂用A、B两种原材料生产甲、乙两种产品。生产1件甲产品需2单位A和1单位B，利润3元；生产1件乙产品需1单位A和3单位B，利润4元。现有A原料10单位，B原料15单位，如何安排生产使利润最大？

【困难】某工厂用A、B、C三种原材料生产甲、乙、丙、丁四种产品。生产每种产品的原料消耗、单位利润及原料总量如下表，且甲产品产量不低于乙产品的30%，丙产品产量不超过丁产品的50%，如何安排生产使利润最大？

产品	A消耗	B消耗	C消耗	单位利润
甲	2	1	3	5
乙	3	2	1	4
丙	1	3	2	6
丁	2	2	2	3
总量	50	40	60

情景②：运输问题

【简单】有2个仓库向3个零售店运送货物。仓库1有100吨，仓库2有150吨。零售店1需80吨，店2需70吨，店3需90吨（不能少于需求量，且库存要清空）。运输成本（元/吨）如下表，如何运输使总成本最低？

仓库/零售店	店1	店2	店3
仓库1	5	6	4
仓库2	3	7	5

【困难】有3个工厂向4个地区配送商品，工厂A、B、C的产能分别为200、300、250件。地区1-4的需求分别为150、200、220、180件。从工厂到地区的运输成本（元/件）如下表，且工厂A到地区1的运输量不超过50件，工厂B到地区4的运输量至少30件，如何运输使总成本最低？

工厂/地区	地区1	地区2	地区3	地区4
A	8	6	9	7
B	5	7	8	6
C	7	5	6	9

情景③：混合配料问题

【简单】

某饲料厂用玉米和豆粕混合生产饲料，要求蛋白质含量不低于15%，粗纤维不超过8%。玉米含蛋白质8%、粗纤维2%，单价1.2元/kg；豆粕含蛋白质40%、粗纤维10%，单价2.5元/kg，并且使得混合原料恰好为100kg，如何配料使成本最低？

【困难】

某化工厂用A、B、C三种原料混合生产100kg产品，要求：纯度≥93%，水分≤3.5%，杂质≤2%。原料成分及成本如下表，且A用量不超过总量的40%，B用量至少是C的1.5倍，如何配料使成本最低？

原料	纯度(%)	水分(%)	杂质(%)	成本(元/kg)
A	98	1	1	8
B	96	2	2	6
C	90	5	5	4

二、非线性规划

（一）适用条件

函数形态和约束条件至少有一个是非线性函数，决策变量为连续实数，但函数可能涉及平方、乘积、指数等非线性项，可能会存在多个局部最优解。

（二）使用情景

情景①：曲线拟合优化：找到非线性曲线拟合数据，使得误差平方和最小

情景②：工程设计优化：设计参数满足非线性约束

情景③：经济均衡问题：涉及边际效应递减的资源分配

（三）典型例题

情景①：曲线拟合优化

例题：某实验室测得一组化学反应数据，时间t（分钟）与产物浓度y（mol/L）的关系如下表。已知该反应符合指数增长模型，其中a、b为待估参数。请通过优化方法找到最佳参数a、b，使模型预测值与实测值的误差平方和最小。

时间t（分钟）	0	10	20	30	40	50	60
浓度y（mol/L）	0	0.6	1	1.3	1.5	1.6	1.

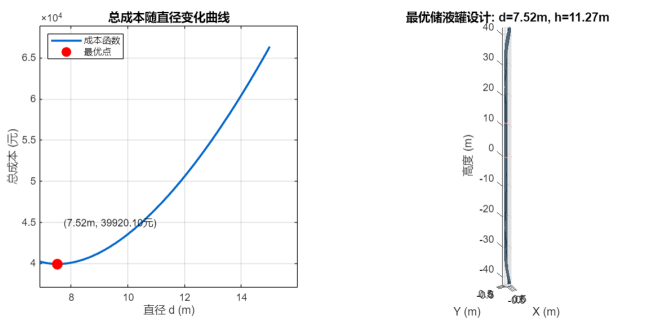
情景②：工程设计优化

例题：某工厂需设计一个圆柱形储液罐，要求容积为500m³。罐壁材料成本为100元/m²，罐底和罐顶材料成本为150元/m²。为保证结构安全，罐高h不得超过直径d的2倍，且直径d至少为5m。如何确定罐的直径d和高度h，使总造价最低？

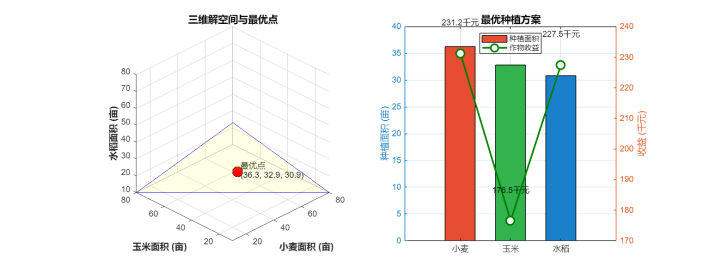
情景③：经济均衡问题

例题：某农场有 100 亩土地可种植三种作物：小麦、玉米和水稻。根据经验，三种作物的收益函数（单位：千元）分别为：小麦：，玉米：

，水稻：，其中 分别为种植面积（亩）。为保证粮食供应多样性，每种作物至少种植 10 亩。如何分配种植面积使总收益最大？

三、整数规划（0-1规划特殊的整数规划）

（一）适用条件

答：函数形态和约束条件是以是线性或者非线性的函数，决策变量为整数（0-1规划是决策变量只能取0或者1）。

（二）使用情景

情景①：选址问题：从多个候选地址中选择若干个建设仓库，满足覆盖需求且费用最低

情景②：背包问题：有限容量的背包中装入若干物品，使得总价值最大

情景③：项目选择问题：从多个项目中选择若干个，在预算约束下最大化收益

情景④：人力资源调度问题：安排不同班次的员工数量，满足需求且总工时最少

情景⑤：指派问题：将n个任务分配给n个人，每人做一项，总效率最高

情景⑥：开关控制问题：电路中开关的通断组合，使得总功耗最低

（三）典型例题

情景①：选址问题

例题：某公司计划在5个候选地址中选择若干个建设仓库，每个仓库的建设成本分别为100、120、90、150、80（万元）。这些仓库需要覆盖8个需求点，各候选地址能覆盖的需求点如下表所示，要求每个需求点至少被一个仓库覆盖，试确定最优的仓库选址方案，使总建设成本最低。

候选地址	覆盖的需求点	成本	候选地址	覆盖的需求点	成本
1	1,2,3	100	4	5,6,7	150
2	2,4,5	120	5	7,8	80
3	3,6	90

情景②：背包问题

例题：一个背包的最大容量为15kg，现有5件物品，其重量和价值如下表所示，每件物品只能选择装入或不装入背包，请问如何选择物品，才能在不超过背包容量的前提下使总价值最大？

物品	重量(kg)	价值(元)	物品	重量(kg)	价值(元)
1	2	10	4	7	42
2	3	15	5	4	25
3	5	30

情景③：项目选择问题

例题：某公司有6个可供选择的投资项目，各项目的投资额和预期收益如下表所示。公司的总预算为60万元，且项目3和项目5互斥（不能同时选择），项目2必须在项目1被选中的情况下才能被选中。请问如何选择项目，才能在预算约束下使总收益最大？

项目	投资额(万元)	预期收益(万元)	项目	投资额(万元)	预期收益(万元)
1	20	25	4	10	12
2	15	18	5	25	30
3	30	40	6	18	22

情景④：人力资源调度问题

【简单】某商店需安排员工值班，每天分3个班次，需求人数分别为：早班6人，中班8人，晚班5人。员工可选择连续工作2个班次（不考虑跨天），如何安排使值班人数最少？

【困难】某医院一周7天需安排护士值班，每天需求人数如下表。护士每周工作5天休息2天（连续或不连续均可），如何安排使总护士数最少？

星期	一	二	三	四	五	六	日
需求	10	8	9	11	12	15	7

情景⑤：指派问题

例题：某公司有4个项目（任务）需要分配给4名员工，每个员工只能负责一个项目，每个项目也只能由一名员工负责。已知各员工完成不同项目的效率（单位：件/天）如下表所示。如何分配任务才能使总效率最高？

员工/项目	项目1	项目2	项目3	项目4
员工1	8	6	10	9
员工2	9	12	7	5
员工3	7	8	11	8
员工4	6	10	9	7

情景⑥：开关控制问题

例题：某电路中有5个开关，每个开关有"接通"和"断开"两种状态。当开关接通时会消耗一定功率并提供相应的电路功能值，如下表所示。开关之间存在约束：开关1和开关2不能同时接通；开关3接通时开关4必须接通；开关5接通时至少要有2个其他开关接通。如何控制开关状态才能在满足所有约束条件的前提下，使总功耗最低？（不能全断开）

开关	接通时功耗	开关	接通时功耗
1	5	4	3
2	4	5	7
3	6

四、规划算法资料包展示

五、规划类算法总结

（一）对比总结

维度	线性规划（LP）	非线性规划（NLP）	整数规划（IP/0-1 规划）
函数形式	目标函数和约束均为线性	至少一项为非线性	通常为线性（非线性更复杂）
决策变量取值	连续实数	连续实数	整数（0-1 规划为 0 或 1）
可行域	凸多面体（连续、凸集）	可能为非凸集（连续）	离散点集（非连续）
最优解特性	存在时必在顶点上	可能有多个局部最优解	需在离散点中搜索
求解难度	低（有成熟高效算法）	高（无通用算法，依赖问题特性）	高（离散性导致搜索复杂）
典型求解算法	单纯形法、内点法	梯度下降法、拉格朗日乘数法等	分支定界法、隐枚举法等

（二）求解器选择

规划类型的求解器有很多，选择正确的求解器对于优化尤为重要。

线性规划

线性规划器选择： % 1. 对偶单纯形法（默认，适合中小问题） % options = optimoptions('linprog', 'Display', 'iter', 'Algorithm', 'dual-simplex'); % 2. 内点法（适合大规模问题） options = optimoptions('linprog', 'Display', 'iter', 'Algorithm', 'interior-point'); % 3. 传统内点法 % options = optimoptions('linprog', 'Display', 'iter', 'Algorithm', 'interior-point-legacy');

整数规划

规划器选择：分支定界法，底层调用线性规划求解器 （1）混合整数线性规划 (MILP) % 使用对偶单纯形法（中小规模） options = optimoptions('intlinprog', 'LPPreprocess', 'basic', 'Display', 'iter', 'RootLPSolver', 'dual-simplex'); % 使用内点法（大规模） options = optimoptions('intlinprog', 'LPPreprocess', 'basic', 'Display', 'iter', 'RootLPSolver', 'interior-point'); 非线性整数规划 (MINLP) %使用遗传算法，复杂非线性问题，全局搜索 options = optimoptions('ga', 'Display', 'iter'); %代理优化，计算代价高的黑箱函数 options = optimoptions('surrogateopt', 'Display', 'iter');

非线性规划

%1.下山单纯形法，适用于变量较少，无约束优化问题 options = optimset('Display', 'iter', 'Algorithm', 'simplex'); x = fminsearch(fun, x0, options);  % 无约束优化 %2.拟牛顿法家族（BFGS、改进的BFGS、DFP） % 无约束优化 (fminunc) options = optimoptions('fminunc', 'Algorithm', 'quasi-newton', ...                        'HessUpdate', 'bfgs', 'Display', 'iter'); % 约束优化 (fmincon)，适合小规模 options = optimoptions('fmincon', 'HessianApproximation', 'bfgs', ...                       'Algorithm', 'interior-point', 'Display', 'iter'); %3.共轭方向法，适合大规模变量 options = optimoptions('fminunc', 'Algorithm', 'trust-region', ...                       'SubproblemAlgorithm', 'cg', 'Display', 'iter'); %4.截断牛顿法，精确二阶导数可用的中大规模问题 options = optimoptions('fminunc', 'Algorithm', 'trust-region', ...                       'SubproblemAlgorithm', 'factorization', ...                       'Hessian', 'user-supplied'); %5.线性近似束优化方法，需要全局优化工具箱 options = optimoptions('fmincon', 'Algorithm', 'interior-point', ...                       'HessianApproximation', 'bfgs', ...                       'SubproblemAlgorithm', 'cg'); %6.序贯最小二乘规划 options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'iter'); %7.信赖域算法 % 无约束版本 options = optimoptions('fminunc', 'Algorithm', 'trust-region', ...                       'Hessian', 'bfgs', 'Display', 'iter'); % 约束版本 options = optimoptions('fmincon', 'Algorithm', 'trust-region-reflective', ...                       'GradObj', 'on', 'Display', 'iter');

关注【小小科研】公众号，回复 {规划算法} 可获取小小科研资料包哦！