Matlab扫频法求系统传递函数

对于一些不好求传递函数的系统，我们还可以使用扫频法来快速获得传递函数，相对于建模法计算的系统传函，扫频法得到的传函进度可能差点。下面以一阶RC滤波电路为例，利用扫频法获取传递函数。

1：在simulink中建立一阶RC低通滤波电路，如下：

2：设置系统的输入和输出

如上图，设置受控电压源的输入为系统输入，电压表的输出为系统输出。

3：打开 Model Linearizer—>ESTIMATION,设置input signal 为正弦输入

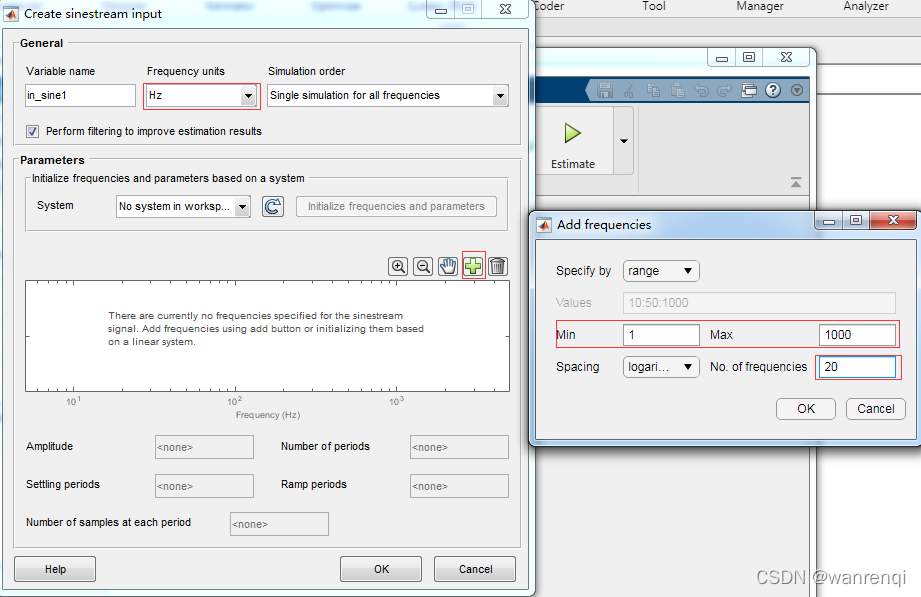
4 :对输入正弦信号的参数进行设置如图：
1：设置输入正弦的单位为HZ；
2：扫频的范围为1HZ~1000HZ；
3：扫频的点数为20个点；

5：所有点设置成一样的参数，Amplitude设置为受控电压源输入的1/10。 如下图：

6：点击Bode，会根据扫描的点绘制出伯德图，同时在Linear Analysis Workspace会生成两个变量； 如下：

6：根据扫频点的响应估算系统传递函数 如下：

我们把上面生成的变量estsys1（扫描点的频率响应）直接拖到 MATLAB Workspace中，然后在MATLAB的命令行中输入sys = tfest(estsys1,n)，n表示系统阶数。这里n为1；

我们根据建模得到的传函为 ：
$$sys=\frac{212.7}{s+212.7}$$
可以看出估算的传函基本和建模的接近。

这里除了用线性分析工具箱外还可以用命名的方式估算系统的伯德图，可以获取更详细的信息。如下：

mdl='RC_Filter';
open_system(mdl); %打开模型 RC_Filter

%%%%%%%%%%收集频率响应的数据

ios = [...      %指定频率响应的输入和输出点
    linio([mdl,'/volin'],1,'input'); ...
    linio([mdl,'/volout'],1,'output')];
f = logspace(log10(10),log10(20000),10);
in = frest.Sinestream('Frequency',f,'Amplitude',1);%使用frest.Sinestream命令来定义要在输入点注入的正弦曲线的频率范围，离散的点数和幅值
[sysData,simlog] = frestimate(mdl,ios,in); %利用frestimate计算频率响应曲线上离散的点
bopt               = bodeoptions;
bopt.Grid          = 'on';
bopt.PhaseMatching = 'on';
figure, bode(sysData,'*r',bopt)

%利用frest.simView命令在一个图形界面中查看注入信号、测量输出和频率响应

frest.simView(simlog,in,sysData);

%估算传递函数
sysA = tfest(sysData,1) %估算一个1阶的传递函数
figure, bode(sysData,'r*',sysA,bopt) %画出这个传函的伯德图

参考文章：https://ww2.mathworks.cn/help/ident/ug/estimating-transfer-function-models-for-a-boost-converter.html
参考模型：https://download.youkuaiyun.com/download/wanrenqi/85033776