厄拉多塞筛法快速求质数 /回文子串

最新推荐文章于 2022-08-01 14:57:49 发布

原创

最新推荐文章于 2022-08-01 14:57:49 发布 · 653 阅读

1 ·

CC 4.0 BY-SA版权

本文介绍了厄拉多塞筛法筛选质数的原理及优化后的暴力算法，同时探讨了回文子串的两种高效算法：动态规划法与中心扩散法，提供了详细的代码实现。

西元前250年，希腊数学家厄拉多塞(Eeatosthese)想到了一个非常美妙的质数筛法，减少了逐一检查每个数的的步骤，可以比较简单的从一大堆数字之中，筛选出质数来，这方法被称作厄拉多塞筛法(Sieve of Eeatosthese)。

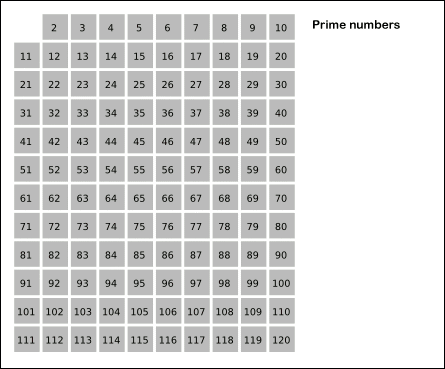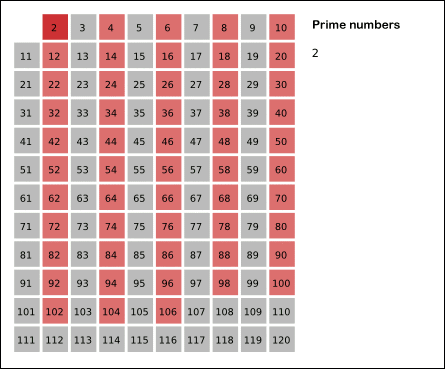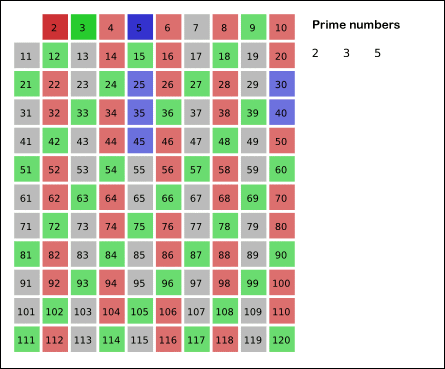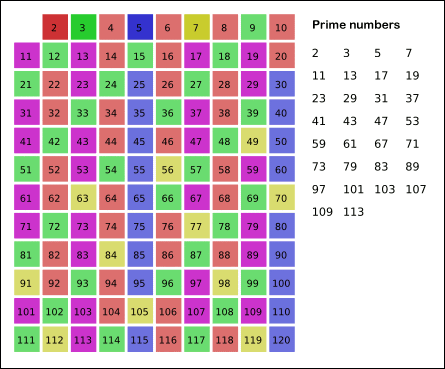
具体操作：先将 2~n 的各个数放入表中，然后在2的上面画一个圆圈，然后划去2的其他倍数；第一个既未画圈又没有被划去的数是3，将它画圈，再划去3的其他倍数；现在既未画圈又没有被划去的第一个数是5，将它画圈，并划去5的其他倍数……依次类推，一直到所有小于或等于 n 的各数都画了圈或划去为止。这时，表中画了圈的以及未划去的那些数正好就是小于 n 的素数。

其实，当你要画圈的素数的平方大于 n 时，那么后面没有划去的数都是素数，就不用继续判了。如下图：

这个介绍摘自 https://blog.youkuaiyun.com/u013291076/article/details/45575967

class Solution {
public:
    int countPrimes(int n)
    {
        int count = 0;
        bool prime[n+1];
        for(int i = 0; i < n; ++i)
        prime[i] = true;

        for(int i = 2; i <= sqrt(n); ++i)   //计数过程 
        {     //外循环优化