1. 引言
无刷直流电机(Brushless DC Motor, BLDC)因其高功率密度、高效率、长寿命等优点,在工业控制、汽车电子、家电等领域得到了广泛应用。然而,传统的六步换相控制方法存在转矩脉动大、噪音明显等缺点,限制了其在高端应用场景的表现。磁场定向控制(Field Oriented Control, FOC),又称矢量控制,通过精确控制电机磁场的方向和大小,实现了类似直流电机的控制性能,成为BLDC电机控制的主流技术。
本文将从基本原理、数学模型、算法实现到实践要点,全面解析BLDC电机的FOC技术,为工程师提供深入理解和实际应用的参考。
2. FOC基本原理与数学模型
2.1 矢量控制核心思想
FOC的基本思想是将电机的定子电流分解为产生磁场的励磁分量和产生转矩的转矩分量,并对其进行独立控制。通过坐标变换,将三相静止坐标系下的交流量转换为两相旋转坐标系下的直流量,从而实现对电机转矩和磁场的解耦控制。
2.2 三相BLDC电机数学模型
在三相静止坐标系(ABC坐标系)下,BLDC电机的电压方程可表示为:
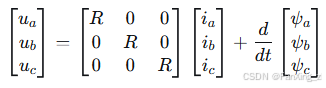
其中,为定子相电压,
为定子相电流,
为定子电阻,
为定子磁链。
磁链方程可表示为:
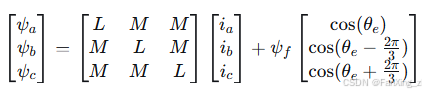
其中,为定子自感,
为定子互感,
为永磁体磁链幅值,
为电角度。
2.3 坐标变换理论
2.3.1 Clarke变换(3s/2s变换)
Clarke变换将三相静止坐标系(ABC)转换为两相静止坐标系(α-β):
逆Clarke变换为:
2.3.2 Park变换(2s/2r变换)
Park变换将两相静止坐标系(α-β)转换为两相旋转坐标系(d-q):
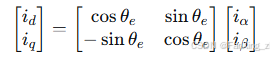
逆Park变换为:
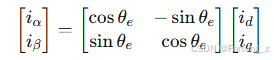
在d-q旋转坐标系下,电机转矩方程简化为:
![]()
对于表贴式BLDC电机(),转矩方程进一步简化为:
这一简化形式直观表明:通过控制即可线性控制电机转矩,这正是FOC技术的核心优势。
3. FOC系统架构与实现
3.1 FOC系统整体架构
完整的FOC系统包含以下关键模块:
-
电流采样与调理:采集电机三相电流
-
位置/速度检测:获取转子位置和速度信息
-
Clarke/Park变换:完成坐标变换
-
PI控制器:实现电流环和速度环控制
-
逆Park变换:将控制量转换回静止坐标系
-
SVPWM模块:生成驱动逆变器的PWM信号
3.2 电流采样技术
准确的电流采样是FOC实现的基础。常用采样方案包括:
-
单电阻采样:在逆变器直流母线上放置一个采样电阻
-
双电阻采样:在两相下桥臂放置采样电阻
-
三电阻采样:在三相下桥臂均放置采样电阻
三电阻采样法具有最高的信噪比和准确性,但成本也最高。在实际应用中需根据系统要求和成本约束选择合适的方案。
3.3 位置检测方法
3.3.1 传感器方案
-
光电编码器:精度高,但成本高且对环境要求严格
-
Resolver(旋转变压器):可靠性高,适用于恶劣环境
-
霍尔传感器:成本低,但精度有限
3.3.2 无传感器方案
对于成本敏感或空间受限的应用,无传感器FOC技术通过检测反电动势或高频注入等方法估算转子位置:
-
滑模观测器(Sliding Mode Observer, SMO)
-
模型参考自适应系统(Model Reference Adaptive System, MRAS)
-
扩展卡尔曼滤波器(Extended Kalman Filter, EKF)
反电动势法的基本观测器方程可表示为:
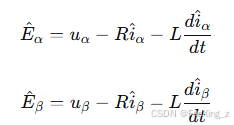
位置估计值为:
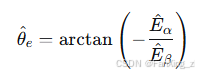
3.4 空间矢量脉宽调制(SVPWM)
SVPWM通过组合逆变器八种基本开关状态,合成逼近圆形旋转磁场的PWM波形,相比传统SPWM具有更高的直流母线电压利用率和更低的谐波失真。
SVPWM实现步骤:
-
扇区判断:根据参考电压矢量
确定所在扇区
-
基本矢量作用时间计算:计算相邻两个基本电压矢量的作用时间
-
PWM信号生成:根据作用时间生成对应的PWM波形
参考电压矢量在α-β坐标系下的表达式为:
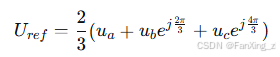
基本电压矢量的作用时间可通过以下公式计算:
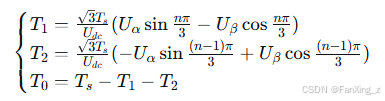
其中,为PWM周期,
为直流母线电压,
为扇区号(1-6)。
4. FOC控制器设计与调节
4.1 电流环设计
在d-q坐标系下,电流环传递函数可简化为:
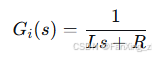
电流PI控制器传递函数为:
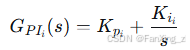
闭环传递函数为:
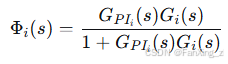
通过零极点对消法,令,可得:
![]()
其中,为电流环带宽,通常取开关频率的1/10~1/5。
4.2 速度环设计
速度环作为外环,其传递函数为:
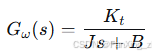
其中,$K_t$为转矩常数,$J$为转动惯量,$B$为阻尼系数。
速度PI控制器参数可通过对称最优法整定:
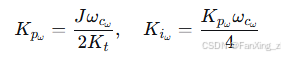
其中,为速度环带宽,通常取电流环带宽的1/10~1/5。
4.3 抗饱和积分(Anti-windup)
在实际系统中,由于电压输出限幅,PI控制器容易出现积分饱和问题。采用抗饱和积分技术可有效解决这一问题:
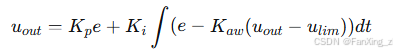
其中,为抗饱和系数,
为限幅值。
5. FOC系统实践要点
5.1 系统初始化与启动
FOC系统启动时需要解决转子初始位置检测和启动平滑性问题:
-
初始位置检测:可采用脉冲电压注入法或IPD(Inductance Position Detection)方法
-
启动策略:
-
对于有传感器系统:直接读取位置信息
-
对于无传感器系统:采用I-f开环控制逐步切换到闭环FOC
-
5.2 参数辨识与自适应控制
电机参数随温度、磁饱和等因素变化,影响控制性能。在线参数辨识可提高系统鲁棒性:
-
定子电阻辨识:注入直流信号测量电压电流关系
-
电感辨识:注入高频信号分析响应特性
-
反电动势常数辨识:基于模型参考自适应方法
5.3 死区补偿
逆变器功率管的开关延迟和死区时间会导致输出电压失真,需进行补偿:
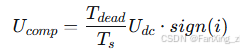
其中,$T_{dead}$为死区时间,$T_s$为PWM周期,$sign(i)$为电流方向符号函数。
6. 性能优化与先进FOC技术
6.1 最大转矩电流比(MTPA)控制
对于内置式永磁电机(IPMSM),通过优化d轴和q轴电流分配,实现在相同定子电流下输出最大转矩:
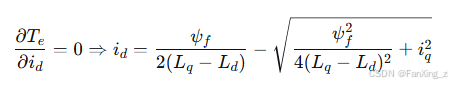
6.2 弱磁控制
当电机转速超过基速时,通过注入负的d轴电流削弱气隙磁场,实现恒功率运行:
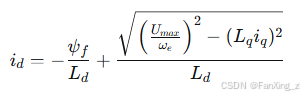
6.3 模型预测控制(MPC)
与传统PI控制相比,MPC通过预测系统未来行为优化控制量,具有更快的动态响应:
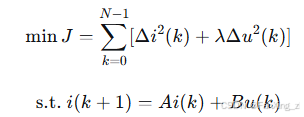
其中,为预测时域,
为控制权重系数。
7. 总结与展望
BLDC电机FOC技术通过精确控制磁场方向,实现了高性能的转矩控制,已成为高端电机应用的标准解决方案。本文系统阐述了FOC的基本原理、数学模型、系统架构和实现方法,并讨论了实践中的关键问题和先进技术。
随着处理器算力的提升和AI技术的发展,FOC技术正向着更智能、更自适应的方向发展:
-
深度学习在参数辨识和控制优化中的应用
-
基于强化学习的自适应控制器设计
-
多电机协同FOC控制
-
与功能安全(ISO 26262)结合的可靠FOC系统
FOC技术的持续演进将进一步拓展BLDC电机的应用边界,为工业4.0、电动汽车、机器人等高端应用提供强劲动力。
参考文献
-
B. K. Bose, "Modern Power Electronics and AC Drives", Prentice Hall, 2002.
-
J. Holtz, "Sensorless Control of Induction Motor Drives", Proceedings of the IEEE, 2002.
-
P. Pillay, "Modeling of Permanent Magnet Motor Drives", IEEE Transactions on Industrial Electronics, 1988.


























深度解析:从理论到实践&spm=1001.2101.3001.5002&articleId=153587411&d=1&t=3&u=e3ae8688662d41568f4f7361a45c4afe)
 2566
2566

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










