梯度下降法

梯度概念有如下特点：
1优良的数学性质特性： 方向是变化率最大的方向，大小是变化率的最大值。
2标量场中鲜明的的几何意义

 

一、书中梯度的定义：

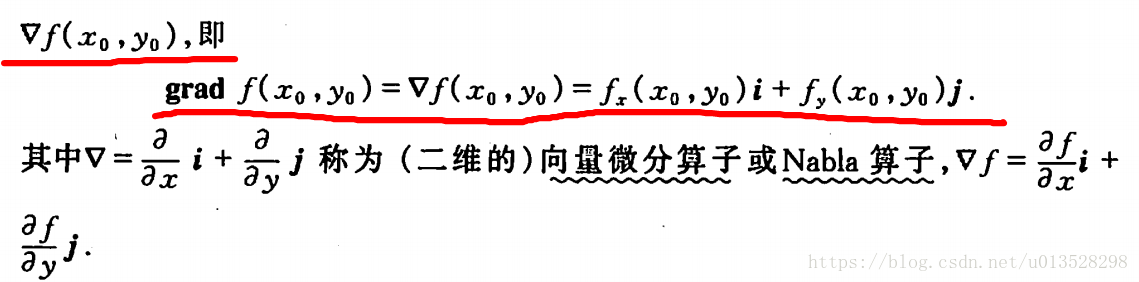
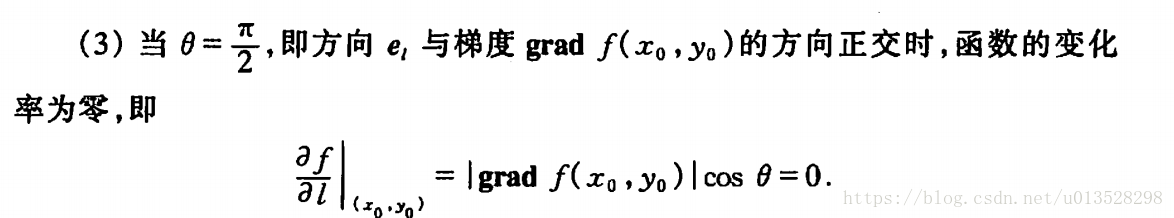
二、梯度直观的理解

1.一元函数时：函数的梯度等于函数的一阶导数

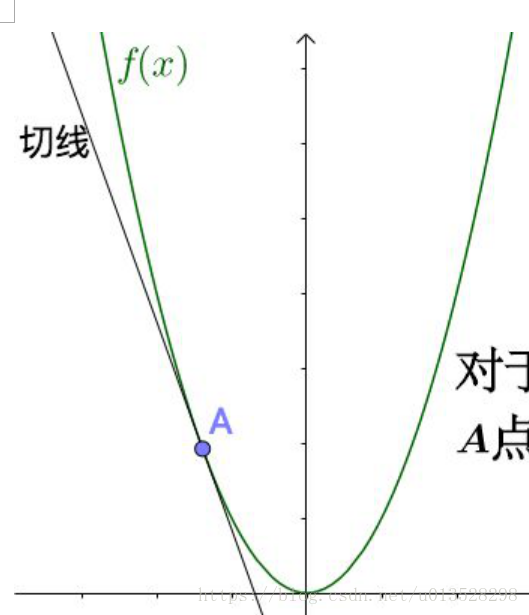
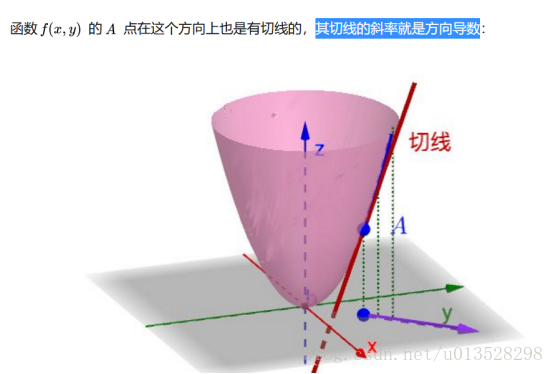
2.多元函数的梯度

 

过A点可以做很多相切的直线，在A点可以有很多方向，可以做很多相切的直线，

每一条相切的直线的就有一个方向导数。

其中梯度是这么定义出来的，梯度是一个向量。

梯度的方向是方向导数里值最大的那个方向导数的方向。

梯度的值是方向导数的最大值

                                               图一

                                               图二

 

Gradient梯度是“升维”操作，梯度符号作用在标量上，得到矢量；梯度符号作用在矢量上，得到张量。
Divergent散度是“降维”操作，散度作用在张量上，得到矢量；散度作用在矢量上，得到标量。

有没有不升不降的操作呢？--旋度。旋度作用在矢量上，还是矢量。[1]

 

 

梯度下降：

通俗易懂了解机器学习中的“回归”和“梯度下降方法”（二）
https://zhuanlan.zhihu.com/p/31167453（里面的梯度下降讲的很好）

参考资料：

[1]

作者：yy gao
链接：https://www.zhihu.com/question/24074028/answer/124997459
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

[2]

图一、图二出处：

https://www.zhihu.com/question/36301367