基于HPSO的低噪声CMOS放大器设计

最新推荐文章于 2025-11-08 13:17:34 发布

原创最新推荐文章于 2025-11-08 13:17:34 发布 · 790 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#HPSO # CMOS差分放大器 # 低噪声设计 # 自动化设计 # 电路优化

使用自动化设计方法的低噪声CMOS差分放大器设计

一、引言

粒子群优化（PSO）[1,2]是一种优化算法，包含一群粒子，通过粒子之间的局部交互以及环境与粒子的全局交互，收敛到最优解。由于易于实现且相关出版物数量最多，PSO非常流行，非常适合在复杂的科学与工程领域中求解优化问题[3]。自动化设计方法分为两类：（i）基于知识的方法和（ii）基于优化的方法。基于知识的设计依赖于设计者的专业知识来制定设计规则，这项工作繁琐、耗时较长，并且仅限于少数拓扑结构，例如：IDAC [4], OASYS [5],等。而基于优化的设计则涉及推导出自动生成设计将电路性能指标作为目标函数，并在一组约束条件下进行优化的流程。该方法在模拟电路设计中具有高度的可靠性和精确性。示例：‐ ASTRX/OBLX [6], DELIGHT.SPICE [7],等。

P. R.A. 武鲁尔 [8]介绍了群体智能在CMOS模拟电路最优尺寸设计中的应用。B.P.德 [9]提出了一种基于ALCPSO的设计方法论，用于n型通道输入折叠式共源共栅运算放大器和带有P型金属氧化物半导体的互补金属氧化物半导体两级比较器的最优设计。O.杰克[10]使用 $g_m/I_D$ 分析方法对BSIM3晶体管模型的热噪声和闪烁噪声进行了分析。根据现有文献可以得出结论：关于实现热噪声最小化的CMOS电路设计在当前研究中仍显不足。

电路中的噪声会限制其处理最低信号电平的能力，从而导致电路性能下降。因此，实现高性能电路需要对噪声进行恰当的分析，并提出降低电路噪声的方法论。目前关于将噪声作为设计规范纳入自动化设计方法论的研究文献较少。本文将噪声作为性能参数之一，与其他电路性能参数一并考虑，从而能够将MOS晶体管的长度和宽度均作为设计变量。所提出的方法论不仅优化了噪声和总电路面积，还深入揭示了噪声与其他电路规格之间的权衡关系。

本文结构如下：第2节描述了采用所提出设计方法论构建电路设计问题的过程；第3节展示了全局最优解的确定及验证过程；最后，第4节给出了论文的结论。

II. 基于HPSO的设计流程

A. HPSO算法

2014年，H. Liu 提出了粒子群优化的变体，称为 HPSO。HPSO 消除了原始粒子群优化中由于种群多样性降低而导致粒子容易陷入局部最优解的情况。为了保持种群的多样性，在速度更新方程中引入了一个称为全局最差粒子的参数，有助于在探索和开发搜索能力。此外，速度更新方程中移除了两个加速系数，从而降低了算法复杂度。HPSO算法的详细描述见 [11]。

B. 设计问题的表述

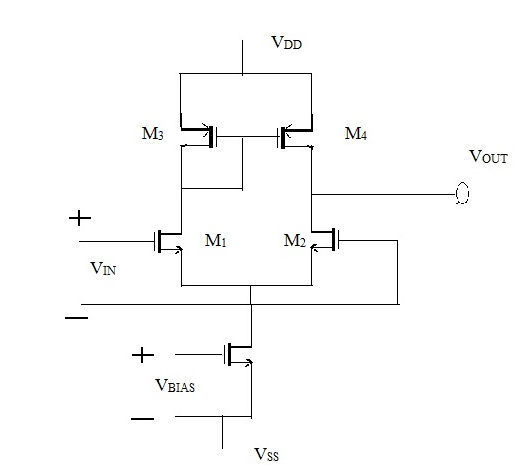
模拟电路的设计涉及选择最优晶体管尺寸，以实现所需或目标电路性能指标的优化性能。尺寸调整技术作为模拟电路设计的一部分，是一个将电路性能指标（目标或约束条件）映射到电路设计参数的构造性过程。换句话说，通过设计参数的取值来评估这些电路规格[12]的性能。因此，为了获得电路的优化性能，需要在不同的约束条件和多目标条件下确定设计参数。在本论文中，我们通过 HPSO优化多个所需的性能指标，主要目标是最小化电路面积和热噪声，设计了一个带有电流镜负载的低噪声 CMOS差分放大器，如图1所示。

示意图0

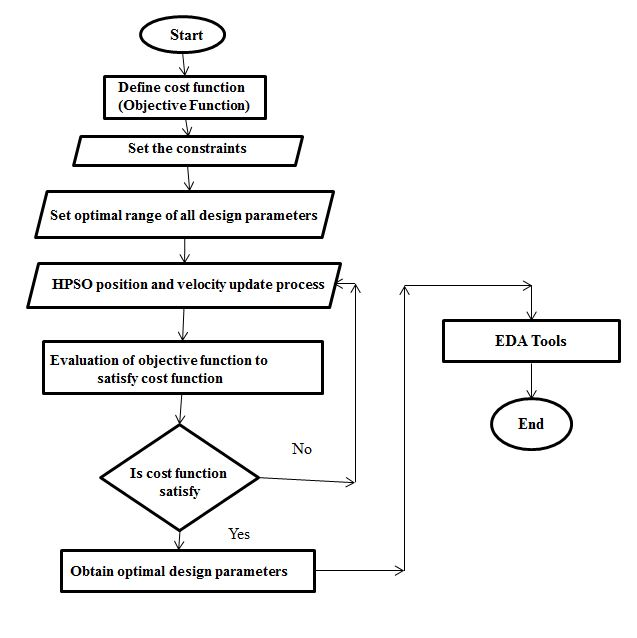
基于HPSO的设计流程从两类信息开始：1st 信息定义了组件，例如工艺、电源和温度，如表I所示。2nd 信息定义了每个设计规范和设计参数的最优范围，如表II所示。我们为电路[8]构建了一个粒子向量结构，该粒子向量结构分为两部分：1st 粒子向量结构用于确定MOS晶体管的最优长度，从而最小化热噪声；而2nd 粒子向量结构则用于其余性能指标。利用MOS晶体管的最优长度，确定满足所有其余约束条件的MOS晶体管最优宽长比。

表I 基于HPSO的设计流程的组件信息

组件	数值
电源电压（V）：VDD，VSS	1.8，-1.8
工艺技术相关（V）：VTN，VPN	0.42，-0.42
工艺技术相关（微安/伏²）：KN，KP	355, 75
温度	300°K

表II 基于HPSO的设计流程的约束条件

设计约束	范围
$(W/L)_k$, k=1-6	100 ≥ $(W/L)_k$ ≥ 3
Lk，k=1-6（μm）	3.5 ≥ Lk ≥ 0.4
转换速率 (V/μs)	≥40
CL(pF)	1.8 ≥ ICMR ≥ -1.5
AV(dB)	≥100
输入共模范围（伏）	-1.5 ≤ ICMR ≤ 1.8

在设计带电流镜负载的低噪声差分放大器时，考虑以下作为约束条件[13,14]的电路性能参数：热噪声、压摆率、频率响应、输入共模范围（ICMR）下限和上限、小信号电压增益。而MOS晶体管的尺寸和负载电容被视为设计参数。

差分放大器的热噪声 [13]
$$
V_{n,in}^2 = \frac{8}{3}kT \left( \frac{1}{g_{m1}} + \frac{1}{g_{m3}} \right) = \frac{8}{3}kT \left( \frac{2L_1}{W_1 K_n’ I_{D1}} + \frac{2L_3}{W_3 K_p’ I_{D3}} \right)
$$
压摆率 (SR)，$I_{D5}$[14] 的确定
$$
SR = \frac{I_{D5}}{C_L}
$$
频率响应 ($f_{-3dB}$, $R_{out}$)[14] 的确定
$$
f_{-3dB} = \frac{1}{2\pi R_{out} C_L}
$$
上输入共模范围（ICMR）($V_{IC(max)}$)，确定 $(W/L)_3$[14]
$$
V_{IC(max)} = V_{DD} - V_{SG3} + V_{TN}
$$
$$
I_{D5} = \frac{1}{2} K_p’ \left(\frac{W}{L}\right) 3 (V {SG3} - |V_{TP}|)^2
$$
下输入共模范围（ICMR），确定 $(W/L)_5$ [14]
$$
V_{IC(min)} = V_{SS} + V_{DS(sat)5} + V_{GS1}
$$
$$
I_{D5} = \frac{1}{2} K_n’ \left(\frac{W}{L}\right) 5 V {DS(sat)5}^2
$$

一个成本函数（CF），所提出的设计方法论必须满足该函数。换句话说，成本函数（CF）是所选或构建的电路的主要目标，即最小化热噪声和总电路面积。

$$
CF_1 = \min(V_{n,in}^2)
$$
$$
CF_2 = \min(T_A), \quad T_A = \sum_{k=1}^{6} W_k L_k, \quad CF_2 \leq 300\ \mu m^2
$$

考虑到描述差分放大器热噪声的公式（1），将 MOS晶体管M1和M3的长度作为设计变量。基于HPSO 的设计流程所采用的初始种群矩阵为10×2 ，其中行数 10表示群集中的粒子（解）数量，列数2表示粒子向量的维度（设计变量）。满足热噪声约束条件的相应粒子向量结构表示为
$$
X_{diff_amp_noise} = [L_1, L_3]
$$
其中，L1 和 L3 分别是MOS晶体管M1 和 M3的长度。

类似地，考虑方程（2-8），所有MOS晶体管的宽度被视为设计变量，即W1-W6。初始种群矩阵取为10×6，其中行数10表示群集中的粒子数量，列数6表示粒子向量的维度（设计规范）。相应的粒子向量结构表示为
$$
X_{diff_amp_per_spec} = [SR, C_L, f_{-3dB}, V_{IC(min)}, A_v, V_{IC(max)}]
$$
其中，SR 是压摆率，CL 是负载电容，f₋₃dB 是截止频率，VIC(min) 是下输入共模范围（ICMR），Av 是电压增益，VIC(max) 是上输入共模范围（ICMR）。

基于HPSO的设计流程用于设计低噪声差分放大器的系统架构如图2所示。

示意图1

III. 优化与Cadence结果

A. 使用HPSO进行优化

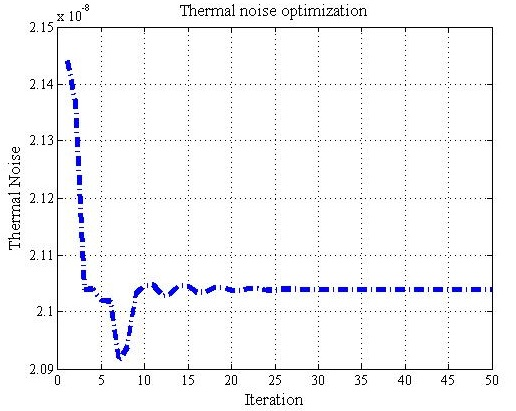
考虑到公式(1)，通过基于HPSO的设计流程进行热噪声优化，以获得使电路中热噪声最小化的MOS晶体管的最佳长度。长度的最优范围取为 ≤3.5 μm [8]，其余参数的值取为 $k=1.38×10^{-23}\ J/K$，$K_1’=355\ \mu A/V^2$，$K_3’=75\ \mu A/V^2$，每个宽度假定在 30–μm 之间。HPSO优化算法运行了50次迭代，并能够收敛到最优解，从而最小化热噪声，在经过25次迭代后，最短时间为0.221秒，如图3所示。通过HPSO算法获得的MOS晶体管长度的最优值和热噪声分别列于表III和表IV中。

示意图2

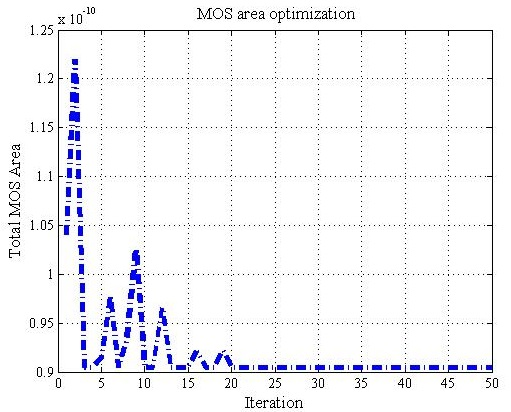
现在，其余性能指标通过基于HPSO的设计流程进行优化，以利用MOS晶体管的最佳长度来获得MOS晶体管的宽度值，主要目标是最小化电路的总面积。我们选择 MOS晶体管M5和M6的长度为1.4微米[8]，并运行 HPSO优化算法进行50次迭代，在满足所有约束条件的同时最小化整个电路。可以看出，HPSO算法在20次迭代后收敛到最优解，图4，最短时间为0.211秒。基于HPSO设计流程在获得全局最优解方面的效率相对于基于IPSO设计流程的效率分别列于表III和表IV中。

示意图3

B. Cadence仿真

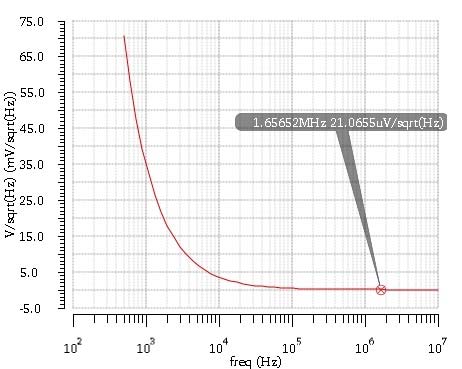
为了验证所提出的设计流程，使用UMC 0.18微米工艺参数技术，在Cadence仿真工具中利用最佳设计参数值对带电流镜负载的差分放大器进行了重新设计。图5展示了通过Cadence仿真获得的差分放大器的噪声分析图，可以看出热噪声在较高频率[13]处达到最小化。因此，基于 HPSO的设计流程能够获得满足差分放大器各项约束条件和目标函数的最优设计参数值。

表III 基于不同算法的设计流程在设计参数上的比较

设计标准	IPSO [8]	HPSO
W₁,W₂（微米）	29.4	7.40
W₃,W₄（微米）	11.3	6.11
W₅,W₆（微米）	2.8	2.8
L₁,L₂（微米）	3.5	3.056
L₃,L₄（微米）	3.5	3.3654

表IV 不同基于算法设计流程的设计规格比较

设计规格	IPSO [8]	HPSO
转换速率 (V/μs)	22.4	11.9
CL(pF)	5	4.4
f₋₃dB（kHz）	100	149.18
AV(dB)	42	41.93
VIC(最大值)(V)	1.4	1.15
VIC(最小值)(V)	-0.8	-0.33
$V_{n,in}^2$ (nV/√Hz @ MHz)	296	21.03
总面积 (μm²)	—	94.19

示意图4

IV. 结论

本文提出了一种基于HPSO的设计方法，用于设计带电流镜负载的差分放大器。所提出的设计方法在设计变量和满足约束条件方面能够获得更优的最优解，且最短耗时仅为0.432秒，从而证明了其相较于另一种知名的基于 IPSO的设计方法具有更高的效率。除了最小化电路中的噪声外，总电路面积也比其他自动化设计方法进一步显著降低。最后，我们使用Cadence对最优设计变量值进行噪声分析仿真，以验证所提出的自动化设计流程。未来的工作中，本文提出的设计方法可用于推导高阶放大器中的多目标优化问题。