96.不同的二叉搜索树 python

最新推荐文章于 2025-03-05 00:15:00 发布
原创 最新推荐文章于 2025-03-05 00:15:00 发布 · 646 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #开发语言 #数据结构 #算法 #leetcode #面试

不同的二叉搜索树

题目

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

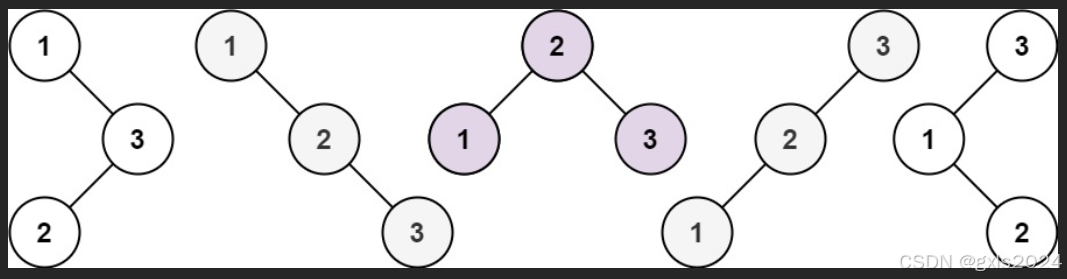
在这里插入图片描述

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

题解

这个问题实际上是在询问具有 n 个节点的二叉搜索树（BST）的不同数目。这个问题可以通过动态规划（Dynamic Programming, DP）来解决，因为它满足最优子结构性质：即问题的解可以由更小规模子问题的解构建而来。

解题思路

对于从 1 到 n 的每个整数 i，我们可以把它作为根节点。那么：

  • [1, i-1] 这些数字会在其左子树中，形成不同的 BSTs。
  • [i+1, n] 这些数字会在其右子树中，形成不同的 BSTs。

因为左子树和右子树都是 BSTs，并且它们的数量仅依赖于节点的数量，所以我们只需要知道对于任意数量的节点能形成多少种 BSTs 就可以了。这正是卡特兰数（Catalan number）的应用场景之一。

因此，我们可以通过以下步骤计算不同 BSTs 的数量：

  1. 创建一个大小为 n+1 的 DP 数组
最低0.47元/天 解锁文章
98. 验证二叉搜索树 Python
小明
03-28 1128
我们只需要遍历二叉树每一个节点，每次更新当前节点对应的范围，然后判断当前节点的值是否位于该范围，就可以知道其是否满足二叉搜索树条件。到这里就能很直观的看出来，每一个节点对应的位置的范围，如果该结点的值在这一范围内，则满足二叉搜索树的条件，反之则不满足。②所有的区间范围都应该是开区间，因为二叉搜索树中不应该存在重复的数值。-1]，我们则需要设置一个超出这个范围的值作为-∞和+∞（本题以-2。①题目要求中所提出，任意结点的值的范围是[-2。[父节点范围的下限，父节点的值][父节点的值，父节点范围的上限]
98.验证二叉搜索树 python
sysu63的博客
02-05 946
要判断一棵二叉树是否为有效的二叉搜索树（BST），可以采用递归的方法，利用每个节点值必须处于一个特定的范围内这一性质。对于BST而言，根节点的值应该大于左子树中任何节点的值，并且小于右子树中任何节点的值。这种方法的时间复杂度为 O(n)，其中 n 是树中节点的数量，因为每个节点都被访问一次。给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。函数来判断给定的二叉树是否是有效的二叉搜索树。解释：根节点的值是 5 ，但是右子节点的值是 4。节点的右子树只包含 大于 当前节点的数。
不同的二叉搜索树（Python版）
fuzzy__H的博客
07-21 341
题目描述 给定一个整数 n，生成所有由 1 … n 为节点所组成的 二叉搜索树 。 解题思路 首先要明确二叉搜索树的重要性质二叉搜索性即一棵二叉搜索树的根节点的值大于左子树所有节点的值，小于右子树所有节点的值，且左子树和右子树也同样为二叉搜索树。假设当前序列长度为 nn，如果我们枚举根节点的值为 ii，那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为 [1…i−1]，右子树的节点值的集合为 [i+1…n]。而左子树和右子树的生成相较于原问题是一个序列长度缩小的子问题，因此我们可以想到用递归的方法来
不同的二叉搜索树（Python）
Heathy__的专栏
03-24 238
不同的二叉搜索树 给定一个整数n，求以1 ...n为节点组成的二叉搜索树有多少种？ 示例: 输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 思路： 先有个列表dp，每个元素对应的索引就是n，值为种类数。dp[2]=2,dp[3]=5，至于dp[0],dp[1]没有意义，但是后面计算会用，设为1不会影响计算。 例子里n是3，还要有一个i从1开始循环到3，依次做根节点。 i=1时：左侧1种情况，右侧2种情况，一共有1*2种情况；dp[0]dp[2] ...
LeetCode 96. 不同的二叉搜索树 | Python
"大梦三千秋的博客
07-15 1182
使用动态规划，解决《LeetCode 96. 不同的二叉搜索树》问题
不同的二叉搜索树 || — Python
梁辰兴的博客
11-27 249
文章目录一、不同的二叉搜索树 ||1.程序简介示例 1示例 2提示2.程序代码3.运行结果 一、不同的二叉搜索树 || 1.程序简介 给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。 示例 1 输入：n = 3 输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]] 示例 2 输入：n = 1 输出：[[1]] 提示
【LeetCode】96. Unique Binary Search Trees 解题报告（Python）
L141210113的专栏
04-18 564
题目分析： 给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？示例:输入: 3，输出: 5 解释:给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 解题思路： 对于一点i，当其为根节点时，左子树的节点的个数为i-1，（为1,…i-1）,右子树的个数为n-i（为，i+1,…n）。对一个根来说，唯一二叉树的个数为左子树结点的个数乘以右子树的个数。而根节点可以从1到n 中选择...
精选资源
树-98. 验证二叉搜索树-PYTHON
01-20
验证二叉搜索树”中，我们需要编写一个Python函数来验证一个给定的二叉树是否符合二叉搜索树的特性。 题目提供了三个不同的解法：递归、迭代以及中序遍历。 1. **递归解法**： 这种方法基于二叉搜索树的性质，将...
leetcode98. 验证二叉搜索树
12-20
在LeetCode的第98题“验证二叉搜索树”中，主要的知识点是如何判断一个给定的二叉树是否符合二叉搜索树（Binary Search Tree, BST）的特性。二叉搜索树是一种特殊的二叉树，其特性是： 1. **节点特性**：对于任意...
LintCode -- 不同的二叉查找树（python-O(n)时间复杂度）
chan15的博客
10-09 907
LintCode -- unique-binary-search-trees(不同的二叉查找树) 原题链接：http://www.lintcode.com/zh-cn/problem/minimum-path-sum/ 给出 n，问由 1...n 为节点组成的不同的二叉查找树有多少种？ 您在真实的面试中是否遇到过这个题？  Yes
python-leetcode-不同的二叉搜索树
Lucy_wzw的博客
03-05 474
【代码】python-leetcode-不同的二叉搜索树。
96. 不同的二叉搜索树 Python
小明
03-22 434
96. 不同的二叉搜索树 Python
96. 不同的二叉搜索树(python)
vs974532452的博客
06-30 304
给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？ 示例: 输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 1 3 3 2 1 \ / / / \ \ 3 2 1 1 3 2 / ...
[Leetcode][python]Unique Binary Search Trees/不同的二叉查找树
蛮三刀酱
07-29 1975
题目大意 给出一个n，求1-n能够得到的所有二叉搜索树 解题思路 转自博客 这题想了好久才想清楚。其实如果把上例的顺序改一下，就可以看出规律了。 比如，以1为根的树有几个，完全取决于有二个元素的子树有几种。同理，2为根的子树取决于一个元素的子树有几个。以3为根的情况，则与1相同。 定义Count[i] 为以[0,i]能产生的Unique Binary Tree的数目， 如果数...
不同的二叉搜索树Python解法
皮_客的博客
03-18 545
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。 例： 输入：n = 3 输出：5 解析： 动态规划，n个节点，提取其中一个节点当根节点，因为每个节点的值不同，但是顺序不能打乱，所以一共可以构成（左子树个数）* （右子树个数），这就分成了子问题，符合动态规划，0个节点所能构成的树是0个但因为要进行乘法梳理，所以设置为1个，相乘起来并不影响，dp[0]=1，dp[1]=1。当有两个节点时，1节点和2节点都能当做根
Leetcode做题日记：96. 不同的二叉搜索树(PYTHON)
weixin_44033136的博客
05-22 192
给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？ 示例: 输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 1 3 3 2 1 \ / / / \ 3 2 1 1 3 2 / ...
LeetCode题目（Python实现）：不同的二叉搜索树 II
RexT1的博客
03-22 659
文章目录题目递归算法实现执行结果复杂度分析动态规划算法实现执行结果小结 题目 给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树。 示例： 输入: 3 输出: [ [1,null,3,2], [3,2,null,1], [3,1,null,null,2], [2,1,3], [1,null,2,null,3] ] 解释: 以上的输出对应以下 5 种不同结构的二叉...
不同的二叉搜索树----LeetCode（Python3实现）
PengFly123的博客
05-22 342
每天LeetCode至少一道题，能量慢慢的 一、题目 题目链接：https://leetcode-cn.com/problems/unique-binary-search-trees/ 给定一个整数n，求以1 ...n为节点组成的二叉搜索树有多少种？ 示例: 输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 1 ...
Leetcode 95. 不同的二叉搜索树 II(Python3)
Aries
02-26 449
95. 不同的二叉搜索树 II 给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。 示例: 输入: 3 输出: [   [1,null,3,2],   [3,2,null,1],   [3,1,null,null,2],   [2,1,3],   [1,null,2,null,3] ] 解释: 以上的输出对应以下 5 种不同结构的二叉搜索树： 1 ...
展示二叉搜索树 python
最新发布
10-02
<think>首先，用户的问题是：“我想查找用Python展示二叉搜索树的方法 请问Python实现二叉搜索树展示的方法”。用户想知道Python中如何展示二叉搜索树，可能指的是如何可视化二叉搜索树的结构，以便更好地理解或调试。 回顾系统指令： - 所有行内数学表达式必须使用$...$格式。 - 独立公式必须使用$$...$$格式并单独成段。 - LaTeX语法正确。 - 使用中文回答。 - 生成相关问题。 - 在回答中引用的段落末尾自然地添加引用标识。 用户提供的引用是关于二叉搜索树的Python实现： - 引用[1]：描述二叉搜索树的基本结构和特点。 - 引用[2]：二叉搜索树的性质和动态集合操作。 - 引用[3]：二叉搜索树的其他操作，如高度、大小、第k小元素、最近公共祖先。 - 引用[4]：二叉搜索树的特性，快速查找、插入和删除操作。 - 引用[5]：二叉搜索树的定义和性质。 这些引用主要集中在二叉搜索树的实现和操作上，但用户问的是“展示”二叉搜索树的方法，意思是可视化二叉搜索树的结构。 在Python中，展示二叉搜索树通常涉及： - 打印树的结构：例如，用缩进表示层级，或使用中序遍历等顺序打印值。 - 可视化工具：使用图形库如Graphviz或PyGraphviz、matplotlib等来绘制树的结构。 我需要构建一个回答： - 结构清晰：逐步解释如何实现展示二叉搜索树。 - 使用中文。 - 添加Python代码示例。 - 在回答中引用相关引用（末尾添加引用标识）。 - 生成相关问题。 步骤： 1. **解释二叉搜索树**：简要介绍二叉搜索树，基于引用。 2. **展示方法**： - 文本方式：打印树的结构（如递归打印）。 - 图形方式：使用可视化库（如Graphviz）。 3. **提供Python代码**：实现一个简单的二叉搜索树类，并添加展示方法。 4. **引用标识**：在相关解释后添加。 5. **生成相关问题**：在末尾。 Python代码示例： - 定义一个BST类，包含插入、搜索等基本操作。 - 添加一个展示方法，比如打印树的结构。 - 对于图形可视化，可以提到使用外部库。 引用相关引用： - 引用[1]和[5]描述BST的基本结构。 - 引用[4]提到有序性，这有助于理解展示。 - 在解释时自然地添加引用。 回答结构： - 开头：介绍二叉搜索树和展示的重要性。 - 主要部分： - 方法一：文本展示（递归打印）。 - 方法二：图形可视化（使用库）。 - 代码示例。 - 结尾：生成相关问题。 生成相关问题： - 基于主题，如BST的其他操作、优化等。 - 例如： 1. 如何平衡二叉搜索树？ 2. BST的搜索时间复杂度是什么？ 3. 如何实现BST的删除操作？ 确保LaTeX：用户问题中没有数学表达式，但如果提到，需用$...$格式。这里可能不需要。 最终回答： - 用中文。 - 清晰、可靠。 </think>### Python实现二叉搜索树展示的方法 二叉搜索树（Binary Search Tree, BST）是一种高效的数据结构，其核心特性是：对于任意节点，左子树的所有节点值小于该节点值，右子树的所有节点值大于该节点值（基于引用[2]和[5]）。这种有序性使得BST在搜索、插入等操作上具有$O(\log n)$的平均时间复杂度（最坏情况为$O(n)$）。在Python中，“展示”二叉搜索树通常指可视化树的结构，以便直观理解其形状和层级。展示方法主要分为两类：**文本方式**（直接打印树的结构）和**图形方式**（使用可视化库生成图像）。下面我将逐步解释这些方法，并提供Python代码实现。 #### 1. 文本方式展示二叉搜索树 文本方式通过递归打印树的结构，以缩进或特定格式表示层级关系。这种方法简单易实现，适合快速调试或文本输出环境（如终端）。核心思想是通过中序遍历或深度优先遍历打印节点值，并添加缩进表示层级（基于引用[4]的有序性特性）。 **Python代码实现**： ```python class TreeNode: def __init__(self, value): self.value = value self.left = None self.right = None class BST: def __init__(self): self.root = None def insert(self, value): if self.root is None: self.root = TreeNode(value) else: self._insert_recursive(self.root, value) def _insert_recursive(self, node, value): if value < node.value: if node.left is None: node.left = TreeNode(value) else: self._insert_recursive(node.left, value) elif value > node.value: if node.right is None: node.right = TreeNode(value) else: self._insert_recursive(node.right, value) def display_text(self, node=None, level=0): """递归打印BST的结构，缩进表示层级""" if node is None: node = self.root if node is not None: self.display_text(node.right, level + 1) print(' ' * 4 * level + '->', node.value) self.display_text(node.left, level + 1) # 示例用法 if __name__ == "__main__": bst = BST() values = [5, 3, 7, 2, 4, 6, 8] for val in values: bst.insert(val) print("二叉搜索树的结构（文本展示）：") bst.display_text() ``` **输出示例**： ``` 二叉搜索树的结构（文本展示）： -> 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 ``` 在这个输出中，缩进表示树的层级（例如，根节点5在顶部）。这种方法利用了BST的有序性，通过右子树优先的遍历确保节点值按顺序打印[^4]。 #### 2. 图形方式展示二叉搜索树 图形方式使用Python可视化库（如Graphviz或matplotlib）生成树的可视化图像，更适合教学或演示场景。Graphviz是首选工具，因为它专为树和图的结构设计（需要安装graphviz库：`pip install graphviz`）。核心步骤包括： - 将BST转换为Graphviz的Dot格式。 - 渲染生成图像文件（如PNG或SVG）（基于引用[3]的实现扩展性）。 **Python代码实现**： ```python from graphviz import Digraph class BST(BST): # 继承上述BST类 def display_graph(self, filename='bst'): """使用Graphviz生成BST的可视化图像""" dot = Digraph(comment='Binary Search Tree') self._add_nodes_edges(self.root, dot) dot.render(filename, format='png', cleanup=True) print(f"图像已保存为 {filename}.png") def _add_nodes_edges(self, node, dot): if node: dot.node(str(node.value), str(node.value)) if node.left: dot.edge(str(node.value), str(node.left.value)) self._add_nodes_edges(node.left, dot) if node.right: dot.edge(str(node.value), str(node.right.value)) self._add_nodes_edges(node.right, dot) # 示例用法（接上） if __name__ == "__main__": bst = BST() values = [5, 3, 7, 2, 4, 6, 8] for val in values: bst.insert(val) bst.display_graph() # 生成名为bst.png的图像 ``` **输出效果**： - 运行代码后，会在当前目录生成一个`bst.png`文件。图像显示根节点5在顶部，左子树（节点3, 2, 4）和右子树（节点7, 6, 8）层级分明。Graphviz根据节点的连接关系自动布局，确保可视化直观[^3]。 #### 方法比较与注意事项 - **文本方式**：优点是不需外部依赖，代码简单；缺点是输出不够直观，适用于小型树。 - **图形方式**：优点是视觉友好；缺点是需要安装graphviz库（安装命令：`pip install graphviz`），且在无图形界面的环境中受限。 - **通用建议**：在实现BST时，展示方法应与基本操作（如插入、搜索）结合。例如，插入后调用`display_text`可实时调试树的结构变化[^2]。二叉搜索树的有序性是展示的核心，确保节点值正确排序以避免误导[^1]。 以上方法都基于Python标准库或常用工具实现，确保可靠性和易用性。如果您需要更复杂的展示（如动画或交互式界面），可扩展使用matplotlib或PyQt等库[^3]。
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

gxls2024

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值