manacher专题

最新推荐文章于 2025-06-19 11:05:16 发布

lemondinosaur

最新推荐文章于 2025-06-19 11:05:16 发布

阅读量587

点赞数

CC 4.0 BY-SA版权

分类专栏： Manacher&回文自动机算法专题文章标签： manacher JZOJ 2682 最长双回文串洛谷 4555 最长双回文串 JZOJ 1950 拉拉队排练洛谷 1659 拉拉队排练

本文链接：https://blog.youkuaiyun.com/sugar_free_mint/article/details/86694606

算法专题同时被 2 个专栏收录

6 篇文章

订阅专栏

Manacher&回文自动机

3 篇文章

订阅专栏

本文详细介绍了Manacher算法，包括其在洛谷3805、4555和1659题目的应用。文章通过分析算法原理，解释如何优化求解最长回文子串、最长双回文串及奇回文串乘积问题，同时提供了相应的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

所讲例题
洛谷 3805【模板】manacher算法
JZOJ 2682 洛谷 4555 最长双回文串
JZOJ 1950 洛谷 1659 拉拉队排练

洛谷 3805【模板】manacher算法

题目

找到一个字符串中的最长回文子串

分析

首先字符串的长度为 $n\leq 11000000$ ，显然只能用 $O (n)$ 的时间完成这道题目，首先朴素的方法就是 $O(n^2)$ ，也就是枚举中间点向外扩展，但是这样的坏处在哪里呢，就是这样扩展很有可能找不到最优解而浪费了时间，那应该怎么做呢?
那就可以引进一种神奇的算法，manacher
那么这是什么神奇的东西呢，首先对于长度奇偶性可以在字符串中间填充分隔符，这样字符串就一定是奇数，为了避免越界，还要在开头加一个分隔符。
那要记录三样东西，首先是 $p [i]$ 表示中点为 $i$ 时的最长回文串的半径，然后那么显而易见答案就是 $max\{p[i]-1\}$ ，那问题是答案怎么算，这是一个大问题
再首先，我们要记录两个东西， $m i d$ 表示当前找到的最长回文串的中点， $m x$ 表示该回文串的右边界。
首先对于每一个 $i$ ，若 $i < m x$ 说明还是有希望的，否则就只能像纯模拟一样 $p [i] = 1$
当然不管怎么样还是得加上这句话 $w h i l e (s [i - p [i]] = = s [i + p [i]]) + + p [i];$
那 $i f (m x < i + p [i]) m x = i + p [i], m i d = i;$ 是为什么，显然可知是更新最长回文子串
但问题是 $m a n a c h e r$ 如何优化呢，那就是 $i < m x$ 的情况了
那么首先设 $j = 2 * i - m i d$ ，也就是对于 $m i d$ ， $i$ 的对称点，可以通过 $(j+i)\div 2=mid$ 得到。
那么分类讨论，首先先配两张图(蓝色所示为j的答案范围，浅绿所示为i的答案范围，区间为mid的答案范围）
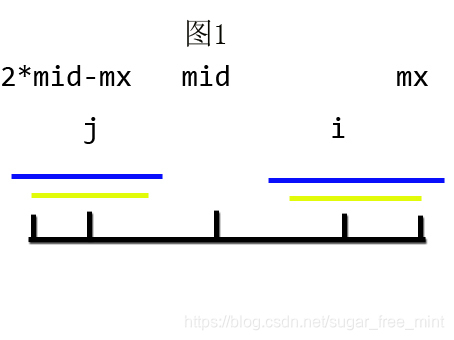
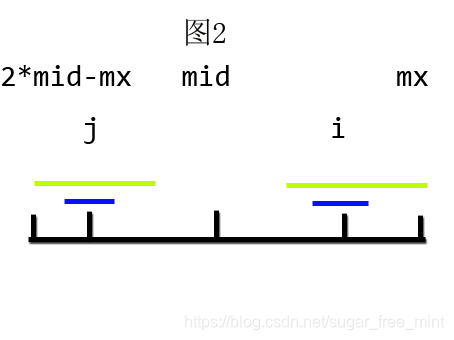
在这里插入图片描述

$j$ 的答案范围超出 $m i d$ 的答案范围,那么如果 $i$ 像 $j$ 那样求答案，就违背了 $m i d$ 的答案，故假设不成立，所以 $p [i] = m i d - i$
$j$ 的答案范围小于 $m i d$ 的答案范围,那么如果 $j$ 像 $i$ 那样求答案，就违背了 $j$ 的答案，故假设不成立，所以 $p [i] = p [j]$
$j$ 的答案范围等于 $m i d$ 的答案范围，则两者均可

综上所述，就可以得到上面的代码

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
char s[22000015]; int n,ans,p[22000015];
inline signed max(int a,int b){return (a>b)?a:b;}
inline signed min(int a,int b){return (a<b)?a:b;}
inline signed manacher(char *s,int len){
    rr int maxlen=1,mx=0,mid=0;
    for (rr int i=1;i<len;++i){
        p[i]=mx>i?min(p[(mid<<1)-i],mx-i):1;
        while (s[i-p[i]]==s[i+p[i]]) ++p[i];
        if (mx<i+p[i]) mx=i+p[i],mid=i;
        maxlen=max(maxlen,p[i]-1);
    }
    return maxlen;
}
signed main(){
    rr char c=getchar(); s[0]='!';
    while (!isalpha(c)) c=getchar();
    while (isalpha(c))  s[++n]='|',s[++n]=c,c=getchar();
    s[++n]='|'; ans=manacher(s,n);
    return !printf("%d",ans);
}

洛谷 4555 最长双回文串

题目

输入长度为 $n$ 的串 $S$ ，求 $S$ 的最长双回文子串 $T$ ,即可将 $T$ 分为两部分 $X$ ， $Y$ ， $（ ∣ X ∣, ∣ Y ∣ \geq 1 ∣ X ∣, ∣ Y ∣ \geq 1 ）$ 且 $X$ 和 $Y$ 都是回文串。

分析

那么在manacher的同时，可以记录最长回文串的最右端的长度 $l [i + p [i] - 1] = p [i] - 1$ 和最左端的长度 $r [i - p [i] + 1] = p [i] - 1$ ,然后用O(n)的时间更新，也就是 $l[i]=max\{l[i+2]-2,l[i]\},r[i]=max\{r[i-2]-2,r[i]\}$ 为什么呢，因为首先最长回文串内的回文子串答案是没有更新的，那为什么要更新呢，因为最长双回文串的两个回文串不一定是最长的，那么统计 $max\{l[i]+r[i]\}$ 即可

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
char s[200015]; int n,ans,p[200015],l[200015],r[200015];
inline signed max(int a,int b){return (a>b)?a:b;}
inline signed min(int a,int b){return (a<b)?a:b;}
inline void manacher(char *s,int len){
    rr int mx=0,mid=0;
    for (rr int i=1;i<len;++i){
        p[i]=mx>i?min(p[(mid<<1)-i],mx-i):1;
        while (s[i-p[i]]==s[i+p[i]]) ++p[i];
        if (mx<i+p[i]) mx=i+p[i],mid=i;
        l[i+p[i]-1]=max(l[i+p[i]-1],p[i]-1);
        r[i-p[i]+1]=max(r[i-p[i]+1],p[i]-1);
    }
    for (rr int i=1;i<=len;i+=2) r[i]=max(r[i],r[i-2]-2);
    for (rr int i=len;i>0;i-=2) l[i]=max(l[i],l[i+2]-2);
    for (rr int i=1;i<=len;i+=2) if (l[i]&&r[i]) ans=max(ans,l[i]+r[i]);
}
signed main(){
    rr char c=getchar(); s[0]='!';
    while (!isalpha(c)) c=getchar();
    while (isalpha(c))  s[++n]='|',s[++n]=c,c=getchar();
    s[++n]='|'; manacher(s,n);
    return !printf("%d",ans);
}

洛谷 1659 拉拉队排练

题目

问前 $k$ 个最长奇回文串长度的乘积

分析

在manacher的基础上开个桶统计长度个数,当然是一个前缀和，因为每个最长回文串其实包含着一些回文子串，然后一定要记得快速幂

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
const int mod=19930726; typedef long long ll;
char s[2000015]; int n,p[2000015],b[2000015];
inline signed max(int a,int b){return (a>b)?a:b;}
inline signed min(int a,int b){return (a<b)?a:b;}
inline void manacher(char *s,int len){
    rr int mx=0,mid=0;
    for (rr int i=1;i<len;++i){
        p[i]=mx>i?min(p[(mid<<1)-i],mx-i):1;
        while (s[i-p[i]]==s[i+p[i]]) ++p[i];
        if (mx<i+p[i]) mx=i+p[i],mid=i;
        if (!(p[i]&1)) ++b[p[i]-1];
    }
}
inline ll ksm(ll x,ll y){
    rr ll ans=1;
    for (;y;y>>=1,x=(x*x)%mod)
        if (y&1) ans=(ans*x)%mod;
    return ans;
}
signed main(){
    rr ll res=1,k;
    scanf("%*d%lld",&k);
    rr char c=getchar(); s[0]='!';
    while (!isalpha(c)) c=getchar();
    while (isalpha(c))  s[++n]='|',s[++n]=c,c=getchar();
    s[++n]='|'; manacher(s,n);
    for (rr int i=n,sum=0;i>0;i-=2){
        sum+=b[i];
        if (k>=sum){
      	    res=(res*(ksm(i,sum)))%mod;
      	    k-=sum;
        }else{
      	    res=(res*(ksm(i,k)))%mod;
      	    k=0; break;
        }
    }
    if (k>0) res=-1;
    return !printf("%lld",res);
}