递归与分形问题

理解分形：递归算法解决图形构造问题

原创已于 2022-03-20 23:07:22 修改 · 2.1k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-03-20 23:03:41 首次发布

第三章专栏收录该内容

9 篇文章

订阅专栏

本文通过三个示例介绍了如何利用递归算法解决分形图形构造问题。从简单的OJ18931分形到复杂的acwing98分形之城，解析了图形自相似性的规律，提供了详细的解题思路和代码实现，帮助读者深入理解分形几何的递归思想。

分形，具有以非整数维形式充填空间的形态特征。
通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。
鉴于“整体缩小后的形状”这一特性，分形问题几乎都是用递归算法来处理。
本文将用三个例子，由浅入深介绍分形问题的解决思路与规律。

（一）OJ 18931 分形

解题思路：题意明确告知，规模N的图形由5个规模N-1的图形组成，因此只要构造了N-1的图形，按某种规律即可得到规模N的图形。
因此，分形问题的本质是发现N和N-1之间的规律，并能通过某种公式表示出来。
由浅入深，1级盒子宽度1，2级盒子宽度3，3级盒子宽度9，可得N级盒子宽度pow(3,N-1)。
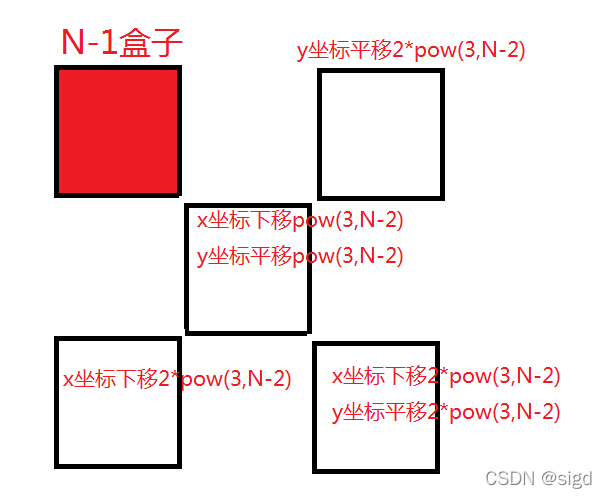
进一步发现坐标规律如下图

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
char a[1005][1005],x;/**< 数组大小根据题意范围设定 */
int m;
void f(int n)
{
    if(n==1)
    {
        a[1][1]='X';
        return ;
    }
    f(n-1);
    int i,j,l=(int)pow(3,n-2); /**< 先构造n-1图形 */
    for(i=1; i<=l; i++) 
        for(j=1; j<=l; j++) /**< 复制4份 */
            a[i][j+2*l]=a[i+l][j+l]=a[i+2*l][j]=a[i+2*l][j+2*l] = a[i][j];
}
int main()
{
    int i,j;
    memset(a,' ',sizeof(a));
    cin>>m;
    f(m);
    for(i=1; i<=(int)(pow(3,m-1)); i++)
    {
        for(j=1; j<=(int)(pow(3,m-1)); j++)
            cout<<a[i][j];
        cout<<endl;
    }
    return 0;
}

（二）洛谷 P1498 南蛮图腾

解题思路：和上题类似，只要构造了N-1的图形，按某种规律即可得到规模N的图形。
N的图形由三个N-1的三角形构成，其中上面的三角形需要向右平移若干单位，读者可尝试自行找到平移规律。注意三角形的底边实际上是2个下划线。
下面两个三角形就是简单复制即可，图形的宽度为4,8,16...即pow(2,n+1)，而高度则是pow(2,n)。

#include <bits/stdc++.h>
using namespace std;
char a[1025][2048];
int f(int n)
{
    int i,j;
    if(n==1)
    { /**< 1级图形只能手敲 */
        a[1][1]=' ';
        a[1][2]='/';
        a[1][3]='\\';
        a[1][4]=' ';
        a[2][1]='/';
        a[2][2]='_';
        a[2][3]='_';
        a[2][4]='\\';
        return 0;
    }
    f(n-1);//先构造小一号的图形
// /\
///__\

    int x=pow(2,n-1),y=pow(2,n);//小一号的图形行列数
// /\
///__\
// /\  /\
///__\/__\

    for(i=x+1;i<=2*x;i++) //先把f(n-1)的图形复制到下面，如上
        for(j=1;j<=y;j++)
            a[i][j]=a[i][j+y]=a[i-x][j];
    for(i=1;i<=x;i++) //最上面那个f（n-1）平移y/2个单位
        for(j=y;j>=1;j--)
            a[i][j+y/2]=a[i][j],a[i][j]=' ';
}
int main()
{
    int i,j,n;
    memset(a,' ',sizeof(a));
    cin>>n;
    f(n);
    int x=pow(2,n),y=pow(2,n+1);
    for(i=1;i<=x;i++)
    {
        for(j=1;j<=y;j++)
            cout<<a[i][j];
        cout<<endl;
    }
    return 0;
}

（三）acwing 98 分形之城

上个大图：

解题思路：同样是找规律，这个规律让人眼花缭乱，对此题目仍感兴趣的朋友请移步

（1）yxc大神的视频讲解：98. 分形之城 - AcWing题库

（2）mob60475706bec5 同学博客中有清晰图示的题解及代码。

（3）某人添加大量注释的代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std; 
pair<ll,ll> calc(ll n,ll x) 
{/**< 分形有四种情况，先根据小一号分形图确定新编号 */
    if(n==0)
        return make_pair(1,1);
    ll cnt=1ll<<(2*n-2),len=1ll<<(n-1);/**< len就是1左移n-1位，相当于pow(2,n-1) */
    pair<ll,ll> ans=calc(n-1,x%cnt==0?cnt:x%cnt);
    if(x<=cnt) /**< 再根据编号所在四个区域分别做转换 */
        return make_pair(ans.second,ans.first); /**< 左上角，x,y互换 */
    else if(x<=2*cnt)
        return make_pair(ans.first,ans.second+len);/**< x不动，y+len */
    else if(x<=3*cnt)
        return make_pair(ans.first+len,ans.second+len);/**< 右下x+len，y+len */
    else
        return make_pair(2*len-ans.second+1,len-ans.first+1);/**< 左下，是小一号图形逆时针再翻转 */
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    ll i,j,n,t,a,b;
    cin>>t;
    while(t--)
    {
        cin>>n>>a>>b;
        pair<ll,ll>p1,p2;
        p1=calc(n,a),p2=calc(n,b);
        int a1=p1.first,b1=p1.second,a2=p2.first,b2=p2.second;
        //cout<<a1<<' '<<b1<<' '<<a2<<' '<<b2<<endl;
        cout<<(ll)(10*sqrt(1.0*(a1-a2)*(a1-a2)+1.0*(b1-b2)*(b1-b2))+0.5)<<endl;
    }     /**< +0.5作用是四舍五入 */
    return 0;
}