力扣第 73 场双周赛 2193. 得到回文串的最少操作次数

最新推荐文章于 2024-11-19 18:17:24 发布

原创最新推荐文章于 2024-11-19 18:17:24 发布 · 400 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #c++

算法专栏收录该内容

35 篇文章

订阅专栏

本文探讨了如何使用贪心策略解决字符串转化为回文问题，通过实例展示了如何在不需要考虑奇偶性的情况下，仅遍历到一半就确定操作次数。重点介绍了奇数长度特殊情况下的交换技巧和模拟交换元素的方法。

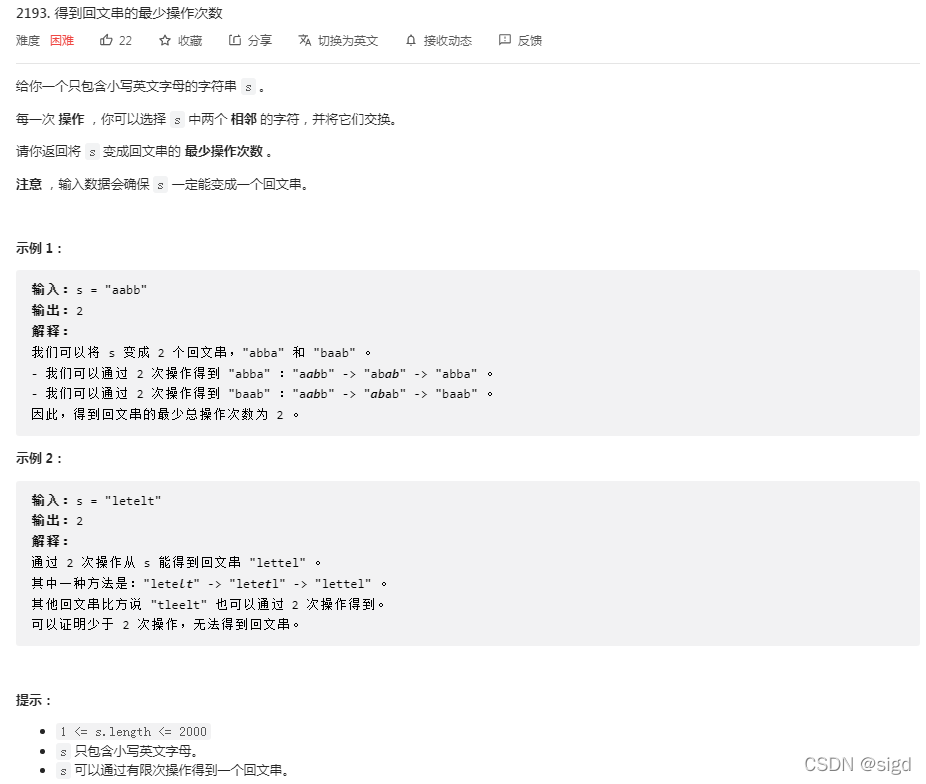
解题思路：贪心。题目确保一定能交换得到回文，首先想到要分两种情况考虑，奇数长度和偶数长度，是否应该计数数组找到奇数长度中点元素？
进一步思考并不需要考虑奇数偶数长度问题，只要按次序处理s[0]....s[n/2]即可。某种特殊情况发生时必然是奇数长度。

class Solution {
public:
    int minMovesToMakePalindrome(string s) {
        int i=0,j,k,n=s.size(),ans=0;
        while(i<(n+1)/2-1)/**< (n+1)/2-1可锁定需要处理的最后一个元素 */
        {
            j=s.size()-i-1;
            while(s[j]!=s[i])
                j--;/**< 找到和s[i]相等的s[j] */
            if(j==i)
            { /**< 特殊情况，s[i]其实是奇数长度中点 */
                swap(s[i],s[i+1]),ans++;
                    continue;
            }
            else
            { /**< 模拟法，交换元素使得s[i]==s[s.size()-i-1] */
                for(k=j;k<s.size()-i-1;k++)
                    swap(s[k],s[k+1]),ans++;
            }
            i++;
        }
        return ans;
    }
};