进化算法优化WSN定位

进化方法在无线传感器网络定位中最小化误差的研究

摘要

无线传感器网络（WSN）中的定位是部署传感器节点及其运行过程中需要高效解决的重要基础需求之一。定位在路由和目标跟踪等依赖位置的应用中是一项具有挑战性的问题。因此，本研究旨在以高精度确定传感器节点的位置。该工作最初基于使用移动锚节点的定位，这是一种用于节点定位的无测距定位方法。当锚节点在网络中移动时，会广播其位置作为信标数据包。传感器节点在收集到来自移动锚节点的足够信标数据包以及来自邻近节点的位置数据包后，即可计算出自身位置。为了提高定位精度，采用了遗传算法（GA）、粒子群优化（PSO）和遗传模拟退火（GSA）等进化算法。本文对定位精度、均方根误差（RMSE）进行了详细研究，并对各种进化方法进行了比较。仿真结果表明，与传统数学方法相比，使用进化算法能显著提高定位精度。结果还表明，在这些进化算法中，GSA在降低定位误差方面最为有效。

关键词 : 定位；无线传感器网络；移动锚点；进化方法；遗传算法；粒子群优化（PSO）；遗传模拟退火

1 引言

无线传感器网络（WSN）是一种自组织网络，通常被称为以数据为中心的网络。它由空间分布的自主传感器组成，用于监测温度、压力、声音、振动等物理或环境条件。传感器之间协同工作，通过网络将其数据传送到一个主要位置（Akyildiz等人，2002年）。由于大量低成本传感器通过相互协作构建网络，且每个节点感知的数据汇聚到基站，因此无线传感器网络（WSNs）无需基础设施。

在新兴传感器网络应用中，为了报告具有地理意义的数据，必须实现传感器节点相对于全局坐标系的定位（Bachrach和Taylor，2006年）。定位是指使传感器网络中的每个传感器节点获知其地理位置的过程（Mao等人，2007年）。若不进行定位，传感器数据将变得毫无意义。定位被视为传感器网络中的一种隐含特性。

最简单的解决方案是为每个传感器节点配备一个GPS（全球定位系统）。然而，由于无线传感器网络（WSN）中的传感器节点数量通常较多，该方案成本较高。此外，这也会使传感器节点更加笨重（Zhu等人，2010年）。目前已有多种用于节点定位的算法，这些算法的基本原理相同：在所有传感器节点中，存在少量节点预先精确知道自身位置（通过预设或安装GPS实现）。算法使用锚节点（具备位置感知能力的节点）（Zenon等人，2007年）来定位其他位置未知的传感器节点。通常，任何定位算法都属于以下两类之一：基于测距的算法和无测距算法。

基于距离的算法使用某些硬件进行定位，而无需距离的算法则利用传感器节点之间传递的消息进行定位。基于距离的算法使用两个节点之间的绝对距离估计或角度估计来进行定位。一些基于距离的算法包括接收信号强度指示（RSSI）（Hoang等人，2011年）、到达时间差（TDOA）（Peng等人，2009年）、到达时间（TOA）（Shen等人，2010年）和到达角度（AOA）（Zhu等人，2008年）。基于距离的方法可提供细粒度精度，但用于这些方法的硬件成本较高。在基于距离的机制中，节点借助额外的硬件获得成对距离或角度（Yu等人，2007年），从而实现高定位精度。由于成本原因，基于距离的方法将不被优先采用。

无测距方法利用来自锚节点和其他节点的消息内容来估计非锚传感器节点的位置。质心算法（邓等人，2008）和距离向量跳数（DV‐Hop）方法（张等人，2009）是某些无测距算法。无测距算法有时使用移动锚节点（帕特罗，2004）进行定位。无测距算法成本不高，但提供粗粒度精度。无测距方案以较低成本提供较低的定位精度。

无线传感器网络中的定位本质上是一个无约束优化问题（张等人，2008）。进化算法是局部搜索方法，能够高效解决复杂的约束或无约束优化问题。所提出的进化方法，如基于遗传算法的移动锚节点定位（MAP‐GA）、基于粒子群优化的移动锚节点定位（MAP‐PSO）以及基于遗传‐模拟退火算法的移动锚节点定位（MAP‐GSA），在利用移动锚节点进行位置估计后应用。本工作采用无测距方法，其中锚节点在移动过程中广播其位置，所获得的定位结果通过上述三种优化策略进行优化。

本文其余部分阐述了该领域的相关研究工作，详细说明了所提出的三种进化算法，并将这些进化算法的性能与现有算法MAP进行了比较。

2 相关工作

廖等人（2011）提出了一种算法（最大后验概率），其中每个传感器节点在其接收范围内接收来自移动锚节点的信标（包含位置信息的消息），当锚节点在感知区域中移动时。在接收到的信标中，传感器节点选择最远的两个信标。该节点以每个选定的信标为中心构建两个圆，圆的半径为传感器节点的通信范围。然后确定这两个圆的交点，并根据决策策略从两个交点中选择一个作为传感器节点的位置。

苏等人（2005）提出了一种无测距算法，该算法基于以下猜想：一条弦的垂直平分线经过圆心。当同一个圆上有两条弦时，它们的垂直平分线将在圆心处相交。一个移动锚点在感知区域周围移动并广播信标。每个传感器节点选择两对信标并构造两条弦。该传感器节点假设自身为一个圆的圆心，并通过求所构造弦的垂直平分线的交点来确定其位置。

张等人（2009）提出了一种无测距算法，其工作方式如下。移动锚点的轨迹沿直线移动。在移动过程中，它周期性地向传感器节点广播其位置。一个传感器节点从所有接收到的信标中选择四个信标。第一组（两个信标）是移动锚节点首次进入该传感器节点通信范围时的位置。第二组是移动锚节点第二次进入该传感器节点通信范围时的位置。在获得这些位置和通信范围后，以所选的四个点为圆心构造四个圆。计算这四个圆的四个交点s1, s2, s3, s4。然后，利用质心公式对这四个交点进行计算，得出该传感器节点的位置。

李等人（2011）提出了用于传感器节点定位的遗传算法，构建了解空间，编码了解，设计了适应度函数，并采用适当的选择机制来选择下一代的父代。通过对个体进行繁殖操作，最终获得了高精度的解。上述遗传算法方法具有良好的定位精度，但解空间非常庞大。该算法在每次迭代中需要搜索大量的解，或者需要较多的迭代次数。因此，当感知区域面积增大时，所需的计算量也随之增加。

前三种方法具有无需额外硬件且仅依赖传递消息的优点，但它们是粗粒度的，即其精度不会很高。

戈帕库马尔和雅各布（2008）提出了一种基于群体智能的方法，用于解决该非线性优化问题中的传感器节点定位。所选择的目标函数是所有邻近锚节点的均方距离误差。粒子群优化算法比模拟退火具有更好的收敛性，并能确保不陷入局部极小值。

吴和陈（2009）提出了一种称为矩形重叠法（ROA）的分布式定位方法，该方法使用配备全球定位系统和定向天线的移动信标。可以根据移动信标的当前状态（包括旋转角度和位置）通过简单操作确定位置。当信标沿直线穿越路径运行后，可准确确定节点位置。

桓祥和勇（2010）提出了一种结合移动锚节点与遗传算法的新型定位方法。该方法将加权质心法与遗传算法相结合。首先，配备全球定位系统的移动锚节点在整個感知区域周围移动，使未知的传感器节点能够获取用于定位的有用信息。然后，通过加权质心法计算未知传感器节点的初始坐标。最后，未知传感器节点的初始位置坐标逐渐收敛到实际坐标。由于遗传算法具有迭代循环特性，定位精度在一定程度上得到提高。

崔等人（2011）提出了一种使用三个移动信标的加权质心定位方法。这些信标在遍历网络部署区域时保持特殊队形，并定期广播其位置。待定位的位置未知的传感器节点估计到这三个信标的距离，并利用加权质心定位方法确定其位置。通过仿真结果表明，该方法优于使用单个移动信标的加权质心定位方法以及三边测量法。

胡等人（2008）提出了一种基于射频的移动锚点质心定位方法（MACL），用于无线传感器网络。在此方法中，移动锚节点在感知区域中移动，并周期性地广播其当前位置。通过使用Cricket定位系统的室内部署进行仿真和测试，以研究MACL的定位精度。根据基于射频的MACL的结果，该方法具有较低的计算复杂度、低通信开销、低成本以及灵活的精度。

卡里姆等人（2010）提出了一种基于移动锚点的无测距节能定位技术（RELMA），特别适用于大规模无线传感器网络，通过最小化所使用的锚节点数量来提高精度和能效。RELMA方法1以及_RELMA_方法2使用每对节点之间的感知范围进行通信，而不是通信范围，以降低节点的功耗。RELMA_方法1和RELMA_方法2的性能仅与现有的基于邻近信息的定位系统（NBLS）进行了比较。仿真结果表明，RELMA方法1和_RELMA_方法2在定位精度和能效方面均优于NBLS。

雷等人（2010）提出了一种基于粒子群优化（PSO）的移动锚点辅助定位算法（MAAAL_PSO），适用于恶劣或危险的应用环境。感兴趣区域（ROI）被划分为网格，移动锚点在每个网格的顶点部署虚拟锚点。基于此部署，节点定位被转化为非线性约束优化问题，并通过粒子群优化（PSO）在移动锚点的协助下求解。性能评估表明，经过少量迭代后，该算法提高了定位精度，并且对环境噪声的干扰具有较强的鲁棒性。

包等人（2012）提出了一种用于具有一或多个移动锚点的无线传感器网络的基于PSO的定位算法（PLA）。PLA不要求移动锚点沿优化或预设路径移动。这一特性使得具有定位能力的移动数据汇聚点可用于数据收集和网络管理应用。仿真结果表明，与质心定位方法相比，PLA在各种场景即广泛条件下均能实现更优的性能。

本文提出的无测距方法采用最大后验概率（MAP）与进化策略。该方法具有高精度和硬件需求少的优点。首先利用移动锚节点对节点位置进行初步估计，然后对所得结果应用MAP‐GA、MAP‐PSO和MAP‐GSA等优化策略。由于解空间较小，引力搜索算法（GSA）无需搜索整个解空间即可估计节点位置，其精度远高于遗传算法（GA）和粒子群优化（PSO）。

3 提出的定位方法

本文所采用的定位策略可分为两个阶段。在第一阶段，传感器节点使用一种名为MAP的无测距算法来确定传感器节点的位置。由于采用了无测距算法（提供粗粒度精度），所确定的位置仅作为一个初步估计，随后在此基础上应用进化策略进一步优化结果。所使用的策略包括基于MAP的遗传算法（MAP‐GA）、基于MAP的粒子群优化（MAP‐PSO）以及基于MAP的引力搜索算法（MAP‐GSA）。

3.1 移动锚点定位（MAP）

仿真环境的设置如下：传感器节点被随机部署在感知区域中。移动锚节点是配备全球定位系统的具备位置感知能力的节点，它们在感知区域内移动。当它们在感知区域内移动时，会周期性地广播包含其当前位置的消息。这类消息被称为信标。所有处于移动锚节点通信范围内的节点都将接收到这些信标。一个传感器节点会收集其范围内的所有信标，并将其存储为一个列表。假设传感器节点与移动锚节点的通信范围相同。当接收到足够多的信标后，如果某个传感器节点未接收到比已接收信标距离更远的信标，则该节点即开始进行定位。

假设传感器节点已接收并将其列表 {T1, T2, T3, T4} 中的四个信标（移动锚点的位置）存储（参见图1）。从该列表中选择距离最远的两个信标（T1, T4），这两个点称为信标点。由于传感器节点未接收到比该点更远的信标，因此这两个点标志着传感器节点通信范围的边界。因此，T1和T4（信标点）要么是同一移动锚点的两个位置，要么是两个不同移动锚节点在位于传感器节点通信范围末端时的位置。

以这两个信标点为圆心，传感器节点的通信范围为半径，构造两个圆（参见图1）。每个圆表示发送该信标的移动锚点的通信范围。传感器节点必须位于此通信范围内，因为它已接收到信标。由于该传感器节点接收到了来自两个锚点的分组，并且这两个锚点位置相同，因此该节点必须同时位于两个圆内。因此，可以得出结论：这两个圆将相互相交。

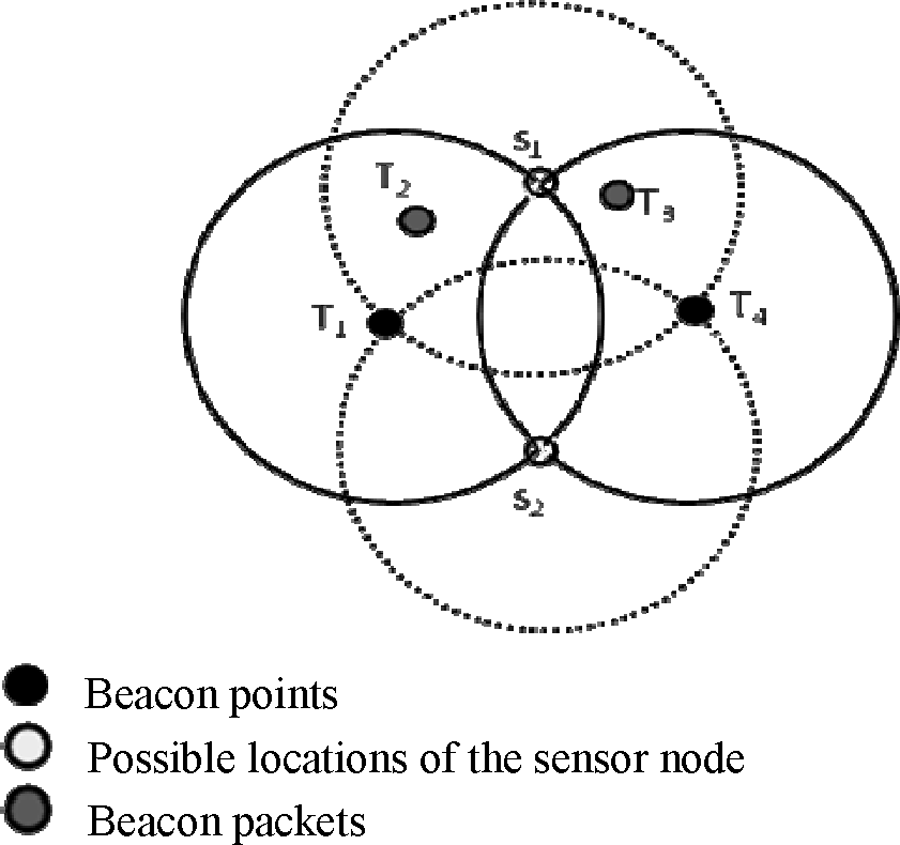
两个圆的交点被确定（S1, S2）。这些交点是传感器节点的可能位置。原因如下：两个最远的点（信标点）是一个传感器节点通信范围的端点。因此，在以移动锚点位置为圆心、节点通信范围为半径的圆中，传感器节点将位于该圆的圆周上。由于与其他移动锚点位置相同，该传感器节点也位于另一个圆的圆周上。因此，该传感器节点位于这两个圆的圆周上。唯一满足上述条件的点是两个交点。因此，通过最大后验概率方法，传感器节点的位置已被近似为两个位置。

3.2 使用进化策略的最大后验概率

第二阶段以传感器节点的两个可能位置作为进化策略的基础。这两个位置是进化策略所需初始种群的基础。通过在两个估计位置及其周围生成染色体来构建初始种群。假设每个传感器节点在移动锚点发送信标时，使用RSSI或TDOA等技术测量其与移动锚点的距离。当测量距离的数量为≥3时，精度会提高。

借助最大后验概率（MAP）大致估计传感器节点的两个可能位置。与使用决策策略从这两个可能位置中确定传感器节点的位置不同，本文采用进化策略来确定节点的位置。所使用的进化策略包括遗传算法、粒子群优化（PSO）和引力搜索算法。每一种上述方法分别应用于最大后验概率，并测量了性能。

在三种策略中，用于迭代的初始种群生成方法、种群中个体染色体的结构、从种群池中为下一代选择父代的方式以及基于适应度函数选择优秀父代的方法基本相同。其机制如下：

遗传编码

为了生成算法的初始种群，需要对种群中每个个体的结构进行编码。由于种群池中的每个个体都是一个候选解，因此将其编码为具有两个基因的实值染色体。第一个基因是表示传感器节点在x轴上位置的实数值，第二个基因是表示其在y轴上位置的实数值。

初始化

解空间在传感器节点的两个可能位置（由最大后验概率确定）及其周围构建，每个个体的结构如上所述。由于最大后验概率已缩小了传感器节点的可能位置范围，解空间较小，因此初始种群规模也较小。

适应度函数

适应度函数决定了个体在下一代种群池中的生存能力（选择）。如前所述，当传感器节点接收到移动锚点的信标时，会测量其与移动锚点之间的距离（通过RSSI等任何技术测量），即传感器节点与锚点之间的实际距离。当锚点位于传感器节点通信范围内的不同位置时，传感器节点会测得多个这样的实际距离。

设“m”为传感器节点与移动锚点之间测得的实际距离数量，此时移动锚点位于不同位置。令di(i = 1 – m)表示传感器节点与移动锚节点之间的实际距离，此时锚节点位于不同位置。最后，(xi, yi)，i = 1 – m，分别是各个移动锚节点的绝对位置或实际位置（通过信标数据包发送的基于全球定位系统的移动锚点坐标）。

设（ai，bi），i = 1 – n，为传感器节点的可能位置（初始种群），其中n为初始种群的大小。

公式(1)给出了种群中个体与移动锚点之间的距离。这是一种估计距离。

$$
\sqrt{(x_i - a_i)^2 + (y_i - b_i)^2}
$$

现在，传感器节点与移动锚点之间的实际距离以及可能解与移动锚点之间的估计距离均可获得。当估计距离与实际距离的差值较小时，意味着该可能解更接近真实位置。基于此，适应度函数被定义为最小化传感器节点与移动锚点之间的估计距离和实际距离之间的差异。该值由以下公式给出：最小值

$$
\sum_{i=1}^{n} \left(\sqrt{(x_i - a_i)^2 + (y_i - b_i)^2} - d_i\right)^2
$$

3.2.1 基于遗传算法的移动锚节点定位（MAP-GA）

如上所述生成初始种群后，进行选择。

选择

在种群池中的个体上进行选择，以选出适合下一代的优秀父代。为种群中的每个个体计算适应度函数。使用适当的选择机制，根据适应度函数选择父代。选定父代后，它们将通过繁殖产生子代，子代进入下一代的种群池中。

繁殖

从选中的父代中选择少量个体；对于每个个体，在任意一个轴上∆d要么被加上，要么被减去。该特定个体的∆d通过(xi, yi)和(aj, bj)计算得出。(xi, yi)是相应移动锚点的绝对位置。(aj, bj)是从种群池中选出的个体，di是传感器节点使用RSSI等方法测得的移动锚点与传感器节点之间的实际距离，对应于相应的(xi, yi)。

$$
\Delta d = \alpha * (\sqrt{(x_i - a_i)^2 + (y_i - b_i)^2} - d_i)
$$

其中，α的取值范围在0到1之间。

变异后，对父代进行单点交叉以产生子代。选择和繁殖过程迭代进行，直到满足终止条件。当种群池中某个个体的距离（适应度函数）差异达到最小时，算法终止，该个体给出传感器节点的位置。

3.2.2 基于粒子群优化的移动锚节点定位（MAP-PSO）

PSO是一种计算过程，通过针对给定的质量度量迭代改进候选解来优化问题。PSO通过拥有一个候选解的种群，并根据数学公式（Gopakumar和Jacob，2008）在搜索空间中移动这些粒子的位置和速度来优化问题。每个粒子的运动受到其局部最优位置的影响，同时也朝着搜索空间中由群体内其他粒子发现的已知最优位置移动。

种群初始化（群体）和适应度函数的计算按前述方法进行。

全局最优

为群体中的每个个体计算适应度函数。选择适应度最高的个体作为群体中其他个体的全局引导，指导每个个体的移动方向。适应度最高的染色体被选为全局最优。

个体最优

个体的最优位置即为个体最优。每当个体位置发生变化时，都会根据该个体的适应度值更新个体最优。

粒子速度

速度定义了粒子在解空间中为获得更优适应度所需移动的距离。每个个体都必须从其迄今为止的最佳位置（个人最佳）向最优解（全局最优）移动。以下方程在个体从局部最优向全局最优移动的程度之间取得平衡。每个粒子的速度通过以下公式计算：

$$
v = v \cdot + c_1 \cdot r_1 \cdot (pbest[\cdot] - present[\cdot]) + c_2 \cdot r_2 \cdot (gbest[\cdot] - present[\cdot])
$$

其中v是粒子在解空间中应移动的最小距离。c1、r1是常数，其取值范围在0到1之间，取决于个体允许从其最优位置移动的程度。c2、r2是常数，其取值范围在0到1之间，取决于个体允许向全局最优移动的程度。current[⋅]是个体的当前位置。

粒子的新位置

群体中每个粒子的新位置通过以下公式计算：

$$
present[\cdot] = present[\cdot] + v[\cdot]
$$

其中，present是粒子的当前位置，v是通过公式(4)计算得到的速度。

在确定粒子的新位置后，会检查该新位置是否为该粒子迄今为止的最佳位置，并在需要时进行更新。一旦群体根据适应度值更新了新个体，就会对全局最优进行更新。当全局最优或某个个体的适应度达到极小值时，该策略结束。

3.2.3 基于遗传-模拟退火的移动锚点定位（MAP-GSA）

GSA是一种将遗传算法与模拟退火相结合的优化算法。GSA充分利用了遗传算法和模拟退火的优点，能够显著提高计算效率。

基于半定规划的定位（SDPL）（李和周，2011）。种群初始化、遗传编码和适应度函数如前所述。下一步进行选择，类似于遗传算法。然后进行繁殖，也类似于遗传算法。

模拟退火

繁殖完成后，确定每个个体的适应度。从种群中选择少量个体。然后对这些被选中的少数个体执行模拟退火。对于每个被选中的个体，其值会进行微小变动（d）。该变动根据适应度值确定如下：

$$
d = c \cdot \text{fitness value of the individual chromosome}
$$

其中，c的值在0到1之间。

新个体的保留决策取决于新的适应度。如果新个体的适应度更高，则新个体将替换旧个体。否则，如果新个体的适应度不如旧个体，则是否保留该个体的决策基于以下公式：

$$
e^{-\Delta d / T} > R(0,1)
$$

其中，R(0,1)是介于0和1之间的随机数，Δd是两个染色体的适应度差值，即变化前个体与变化后个体的适应度之差，T是温度。在初始阶段，T具有较高的值，随着迭代次数增加而逐渐降低。这允许在初期选择适应度较低的个体（承担风险以实现更快收敛），但随着迭代次数增加，此类个体将不允许存在于种群中。如果上述条件满足，则选择该个体。

与在解空间中进行全局搜索的遗传算法不同，模拟退火进行局部搜索。引力搜索算法结合了二者的优势。遗传算法通过大跨度跳跃使个体在解空间中接近实际位置，而模拟退火则通过对适应度较高的个体进行小幅度移动，使其更接近实际位置。

4 仿真结果

通过对MAP进行的各种仿真研究，以下场景被证明是提供最小定位误差的最优配置。因此，在所有优化策略应用于MAP时，均保持如表1中所述的以下设置。移动锚节点根据移动文件中指定的位置数据在感知区域内移动，该移动文件作为输入提供给NS2模拟器。

在上述仿真设置下，通过比较MAP与MAP‐GA对结果进行了分析。类似地，还通过比较MAP与MAP‐PSO的性能以及MAP的性能对结果进行了分析使用MAP‐GSA进行仿真。MAP及这三种进化策略的仿真在NS‐2中完成，图形由Gnuplot绘制。

参数	设置
传感器节点数量	100
传感区域面积	1000 × 1000米²
移动锚节点数量	3
移动锚节点速度	100 米/秒
连续信标之间的时间间隔	0.5 毫秒
执行时间	500 秒
传输范围	250米
代数	10–60

根据使用三种进化算法在定位过程后获得的结果，这些结果被用于绘制以下内容：
- 使用最大后验概率的实际位置和计算位置的图
- 使用最大后验概率及三种进化算法的实际位置与计算位置的对比图
- 仅使用最大后验概率与结合三种进化算法使用最大后验概率时，实际位置与计算位置之间距离的定量差异
- 展示了最大后验概率的均方根误差（RMSE）与三种进化算法相比的结果图。

所使用的性能参数是传感器节点的实际位置与计算位置之间的距离差异（DD），以及用于估计定位误差的均方根误差（RMSE）值。

传感器节点的实际位置与计算位置之间的DD定义为

$$
DD = \sum_{i=1}^{n} \left( |Xai - Xci| + |Yai - Yci| \right)
$$

其中（Xai，Yai）和（Xci，Yci）分别表示传感器节点i的实际位置与计算位置之间的距离差异，n表示节点编号。用于计算均方根误差（RMSE）的公式定义为

$$
RMSE = \left{ \frac{1}{N} \sum_{i=1}^{n} \left[ (Xai - Xci)^2 + (Yai - Yci)^2 \right] \right}^{1/2}
$$

其中（Xai，Yai）和（Xci，Yci）分别表示传感器节点i的实际位置和计算位置，i的取值范围为1到N。

4.1 计算位置与实际位置对比图

紫色矩形显示传感器节点的实际位置。绿色三角形显示计算出的位置使用MAP以及使用MAP‐GA来确定位置。可以观察到，在第二种情况（图3）中，对于许多传感器节点，计算位置几乎与实际位置重合。而在第一种情况（图2）中，很明显仅使用MAP方案时，只有少数传感器节点非常接近其实际位置。

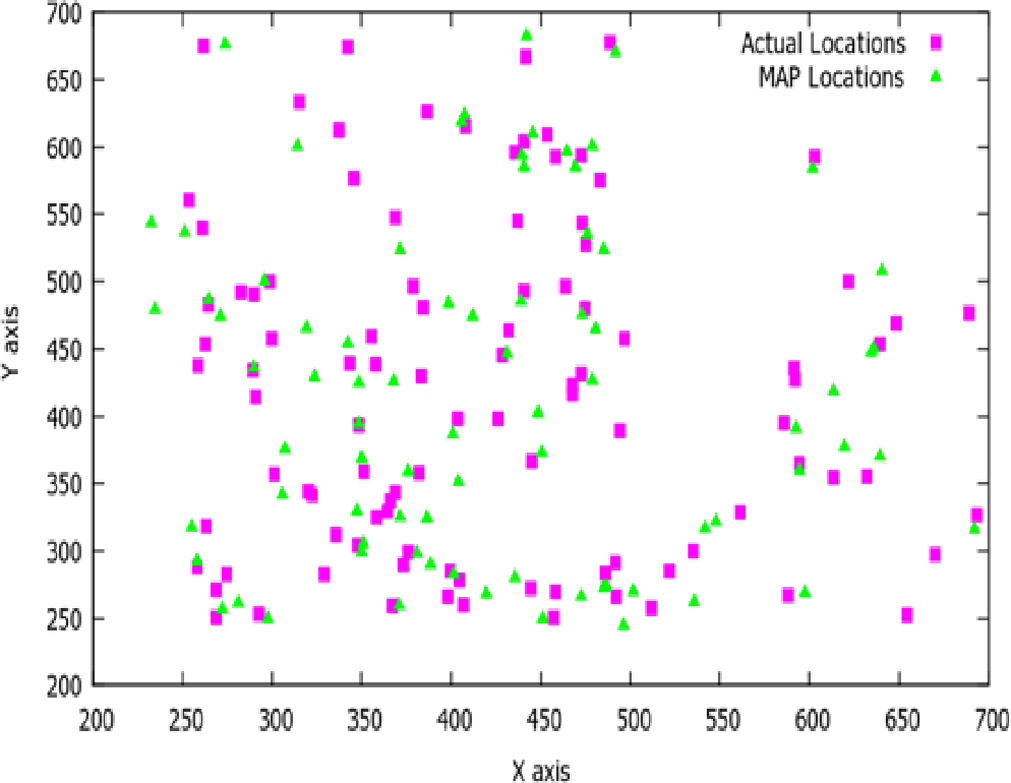
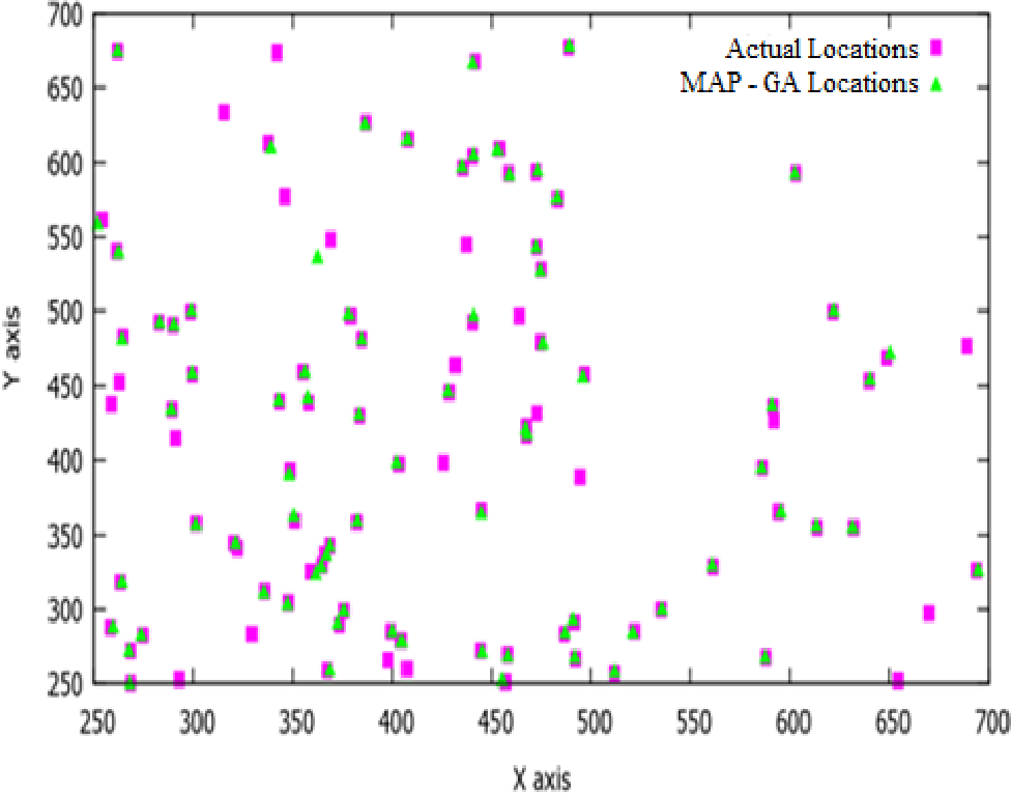
图4中的图表显示，通过使用粒子群优化算法，定位效果得到了显著提升。同时还可以观察到，在定位过程中，与使用遗传算法相比（图3），计算位置更接近原始位置。

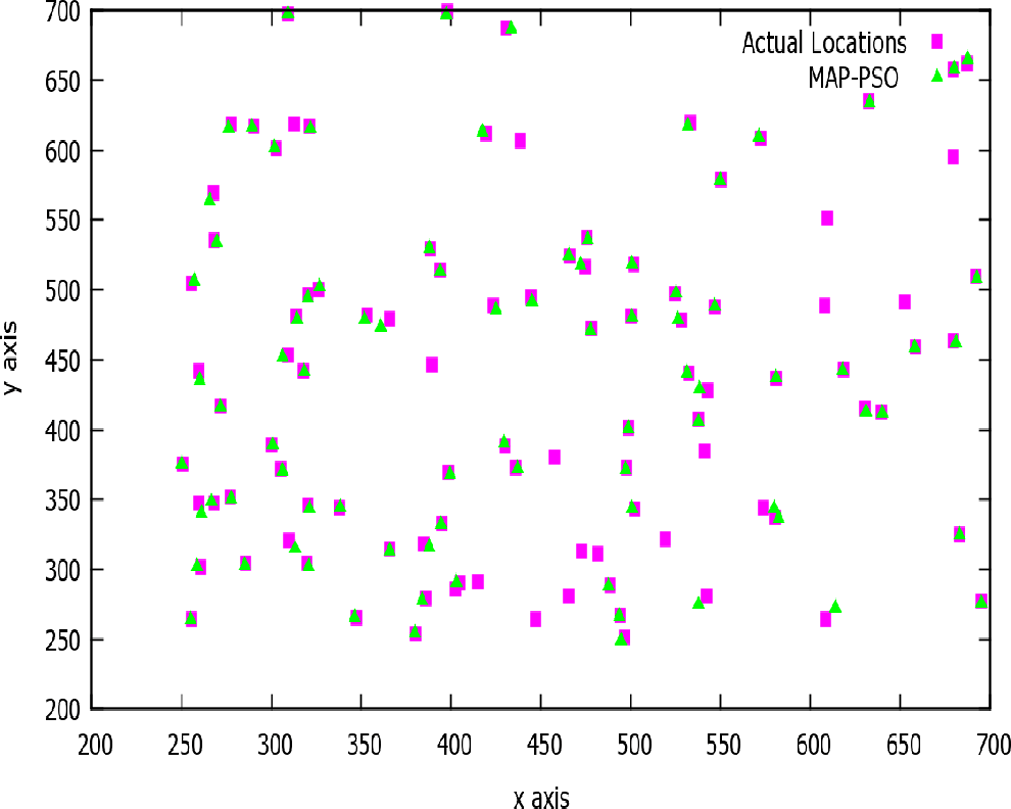
图5中的曲线图说明了引力搜索算法在定位中给出了最佳的优化结果。可以观察到，传感器节点的计算位置或多或少与实际位置重合。

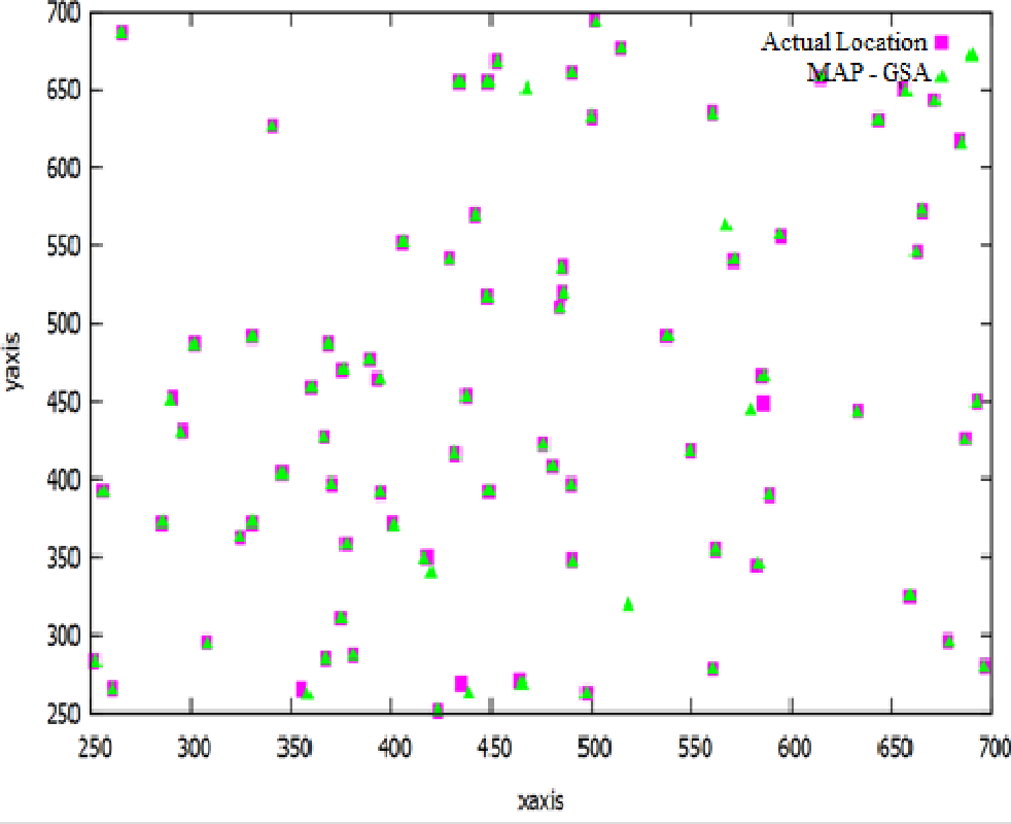
基于最大后验概率（MAP）结合引力搜索算法的定位（图5）所产生的误差最小，相较于基于最大后验概率结合遗传算法（图3）或最大后验概率结合粒子群优化（PSO）（图4）的定位策略而言。

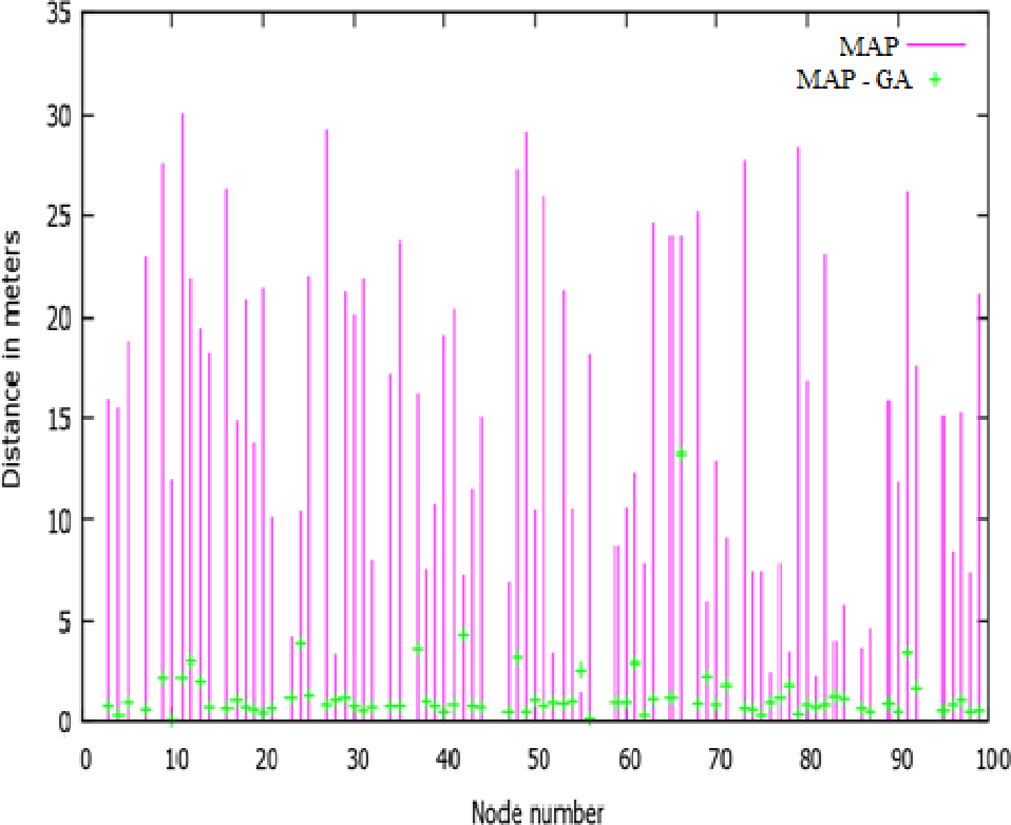
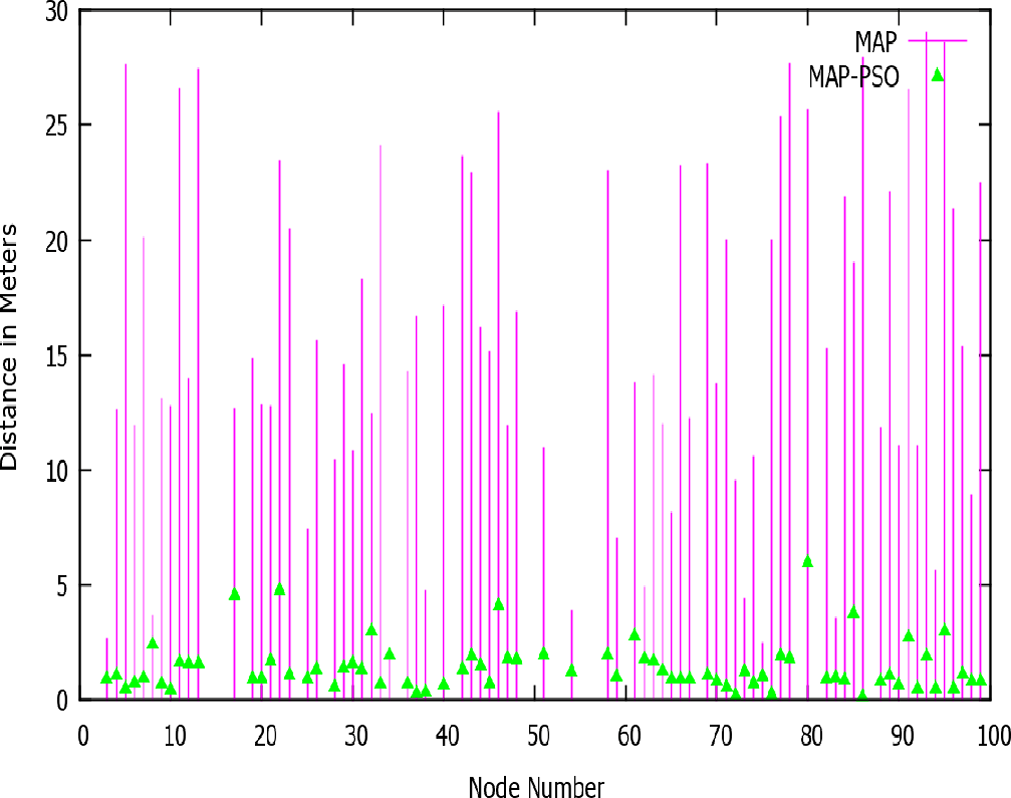
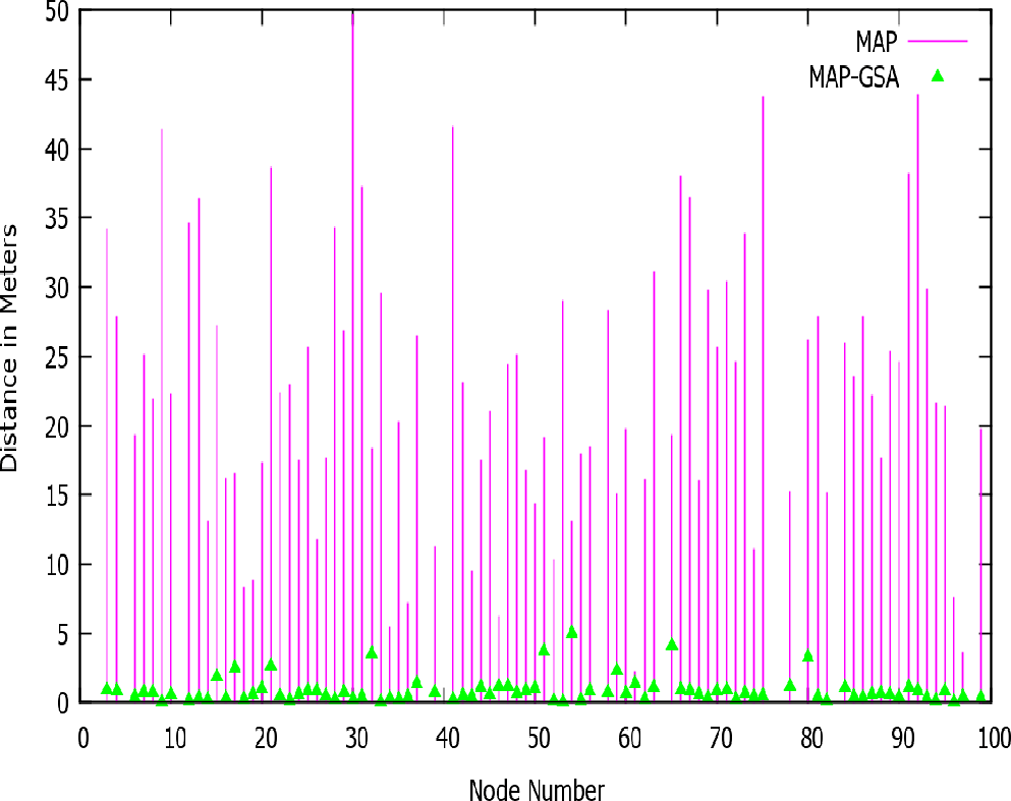
图6–8中的图形显示，脉冲信号（紫色线）表示实际位置与通过最大后验概率得到的计算位置之间的距离差异。脉冲信号上的点（绿色点）表示使用优化策略时实际位置与计算位置之间的距离差异。

4.2 计算位置之间距离差异的图示

从这些图表中可以看出，使用进化策略的MAP与未使用进化策略的MAP之间的距离差异较大。因此可以得出结论，只有在使用进化策略时，定位误差才会显著降低。

4.3 均方根误差（RMSE）图

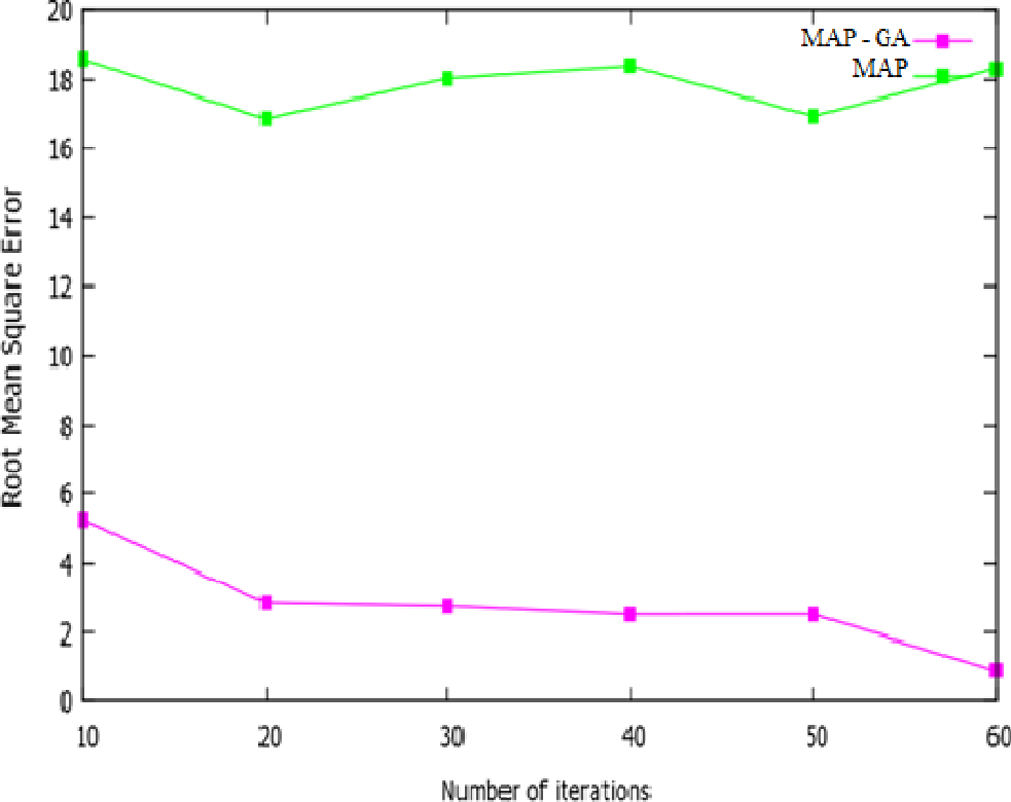
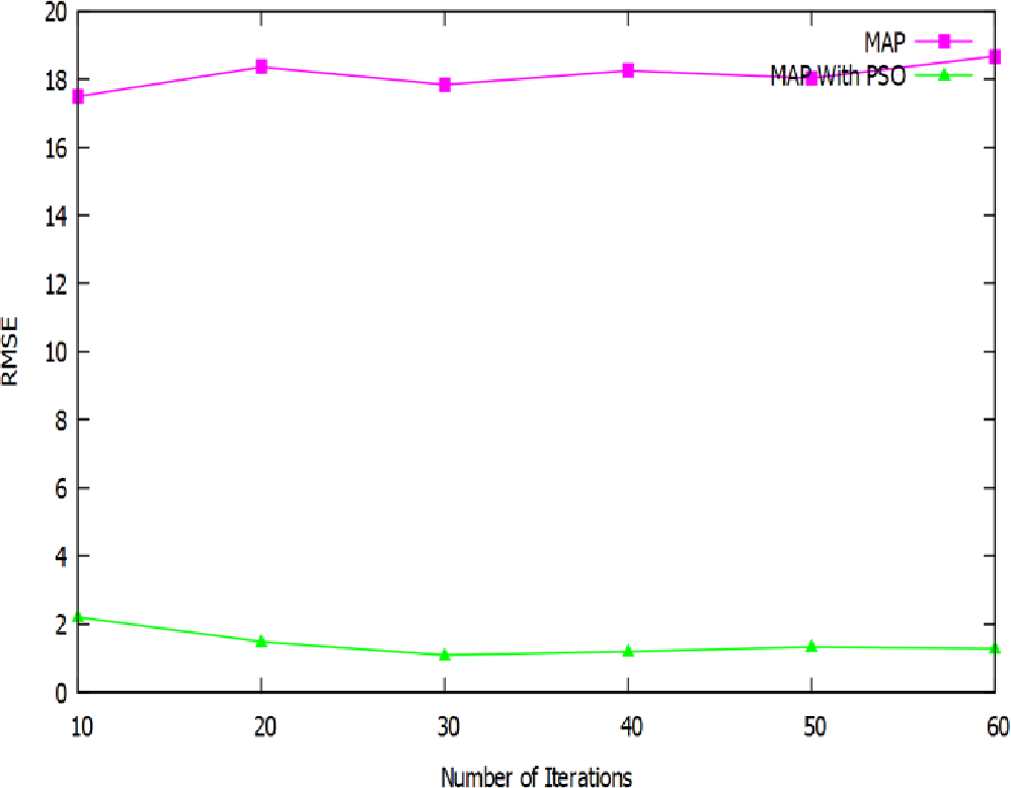
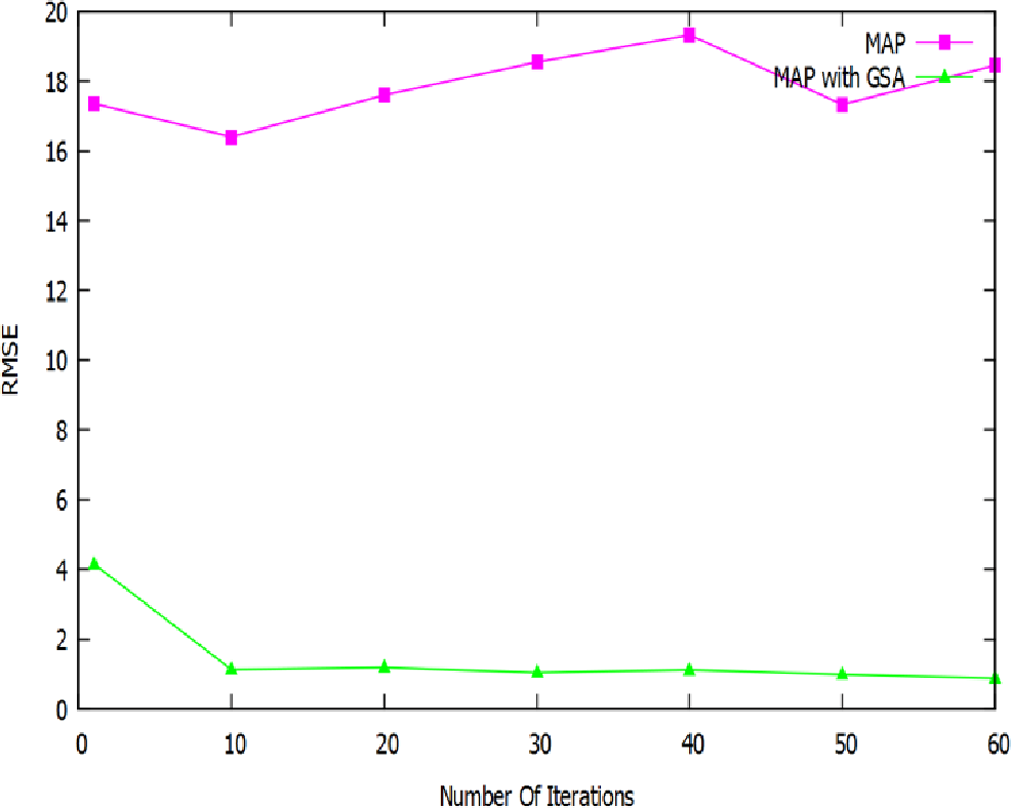
图9–11中的三个图表展示了优化策略以及最大后验概率（MAP）的均方根误差（RMSE）。x轴表示迭代次数，而y轴表示相应的误差。MAP与迭代次数无关，而进化策略则依赖于迭代次数。无论迭代次数如何，MAP的RMSE值始终在16–19范围内。对于遗传算法（GA），RMSE值从6开始，随着迭代次数增加降至1，达到最低值。而粒子群优化（PSO）的最大RMSE为2，随着迭代次数增加降至其最小值1；引力搜索算法（GSA）的RMSE值起始值为1。即使GSA仅执行一代，其RMSE最大值也仅为4，低于GA，并且当迭代次数达到60时，RMSE几乎接近零。因此，可以明显看出GSA在定位中提供了最佳的优化结果。

5 结论

从仿真结果可以得出结论，最大后验概率是一种高效的定位算法，因为它不需要额外的硬件，仅使用消息进行定位，消息传递不要求传感器节点洪泛接收到的数据包，并且已定位节点的百分比很高。尽管最大后验概率是一种高效的定位算法，但与采用进化策略优化的最大后验概率相比，其定位误差较高。

当使用遗传算法作为优化策略时，定位误差降低了84%（通过百分比误差公式计算）。MAP‐PSO将定位误差降低了88%，而MAP结合GSA则降低了91.5%。因此，可以得出结论：与单独使用MAP相比，结合进化策略的MAP效果更优。然而，在各种进化策略中，GSA对定位过程的优化优于其他两种进化策略。遗传算法提供的全局搜索以及模拟退火所提供的良好局部搜索收敛性，使其成为无线传感器网络定位中最优的优化策略之一。

此外，遗传算法还可以与其他进化策略相结合，形成新的混合遗传算法，并可将其定位误差与纯遗传算法（即MAP‐GA）以及MAP‐GSA进行比较。