基于强化学习的车载数据转发

一种基于强化学习的车载网络数据转发方法

摘要

作为车载自组织网络的基础，数据转发方法是确保网络通信稳定性和效率的最重要部分之一。然而，高速移动的车辆节点导致网络拓扑频繁变化以及网络链路断开，给网络数据传输性能带来了巨大挑战。基于车辆轨迹先验知识的数据转发方法难以适应现实应用中不断变化的车辆轨迹，而通过广播方式获取目的车辆位置的开销极高。为解决上述问题，我们提出了一种基于关联状态的优化数据转发方法（ASODF），并在低负载路侧单元（RSU）的辅助下实现。该方法将城市道路网络映射为有向图，利用携带转发机制，并将数据传输分解为在交叉路口的决策式数据转发和在道路上的数据传输。携带数据的车辆将通过低负载路侧单元获得的目的节点位置与其自身位置结合，形成关联状态，并将关联状态优化问题建模为一个基于马尔可夫决策过程（MDP）的强化学习问题。我们采用值迭代方案求解延迟最优策略，并进一步用于转发数据包，以实现最优的数据传输延迟。基于真实车辆轨迹数据集的实验验证了我们提出的ASODF模型的有效性。

1 引言

随着车辆信息技术的提升和无线通信技术的发展，车载自组织网络（VANET）迅速发展。VANET 是一种基于移动自组织网络（MANET）专门设计用于车辆间通信的自组织网络。VANET 中的通信可分为三种类型，包括车对车（V2V）、车对基础设施（V2I）和基础设施对车（I2V）。车载网络的核心在于由车辆和路侧单元组成的网络中数据传输的速度、效率与安全性。然而，节点数量多且移动速度快的特点使得有效路由的使用变得困难。

互联网和无线传感器网络中的协议算法，例如文献[1]提出了安全蜂窝中继路由协议，还包括一些现有的无线传感器网络中的密钥管理方案[2]，例如，Duet 等人提出了一些密钥管理方案[3,4]。此外，针对无线传感器网络问题的其他现有研究在文献[5]中进行了阐述，以及文献[6]中提出的时间同步方案也无法应用于车载自组织网络。此外，网络性能对数据传输机制至关重要，因为网络性能受到许多因素的影响，包括信道质量的不稳定性和不确定性。因此，已提出一些特定方法来解决这些问题。

车载网络中的现有数据传输方法可分为三类。第一类是基于拓扑的方法。此类方法又可分为两个子类：主动式和反应式。Destination Sequenced Distance Vector (DSDV)[7] 和 Optimized Link State Routing protocol (OLSR)[8] 是两种经典的主动式方法。这类方法的一个明显缺点是节点需要随时更新路由信息，消耗大量带宽。Dynamic Source Routing (DSR)[9] 和 Ad hoc on Demand Distance Vector routing (AODV) 是两种反应式方法。但由于使用广播模式，DSR 的可扩展性较差，不适合大规模的移动自组织网络。AODV 能适用于大规模网络，但仍存在一些问题，例如较大的网络开销和路由过期问题。

其次，由于车载自组织网络（VANET）具有拓扑频繁变化的特点，网络节点很难建立和维护稳定的路由表。因此，基于拓扑的数据传输方案不适用于车载网络。随着GPS设备的普及，基于地理位置的数据传输方法被提出。贪婪周边无状态路由 (GPSR)[10] 和地理源路由 (GSR)[11] 是两种基于地理位置的方法。GPSR使用贪婪模型进行数据传输，存在局部最优问题。GSR不同于这些节点可随机移动的模型，它利用了车辆只能在道路上行驶的特性。因此，数据传输只能在交叉口发生。GSR未考虑道路网络中的实时交通状况，可能导致所选道路路段上车辆过少而造成连接性不足。

第三，由于车载自组织网络中网络链路的频繁断连以及无法建立从源节点到目的节点的端到端路由，研究人员创造性地将容忍延迟网络和机会网络的机制引入车载网络，提出了一种基于存储‐转发和携带转发机制的数据传输方案。Static Node Assisted Adaptive Routing (SADV)[12] 和 Vehicle Assisted Data Delivery (VADD)[13] 是两种基于存储‐转发机制的方法。SADV在交叉口部署静态节点，即路侧单元（RSU），以协助数据传输。SADV借鉴了VADD的路段延迟模型和最优路径选择。SADV利用存储‐转发和携带转发机制，使其具有较高的效率数据路由解决方案。然而，由于需要在每个交叉口部署基础设施，SADV 不适用于大规模网络环境。VADD 是一种为稀疏环境提出的方法。首先，VADD 从真实的车辆轨迹数据中提取延迟模型。然后，VADD 根据延迟模型计算数据包从当前交叉口到目的节点经过相邻路口的总延迟。最后，VADD 对总延迟进行排序以选择最优路由。

第四，基于存储‐转发和携带转发机制的模型是解决因车辆稀疏导致链路断开问题的有效方案。但这些模型仍未考虑由车辆特定轨迹引起的道路限制和人类行为模式。因此，提出了基于车辆轨迹的模型。这些模型可分为两类：一类是车辆轨迹预先固定的模型；另一类是基于轨迹预测的模型。基于锚点的街道与交通感知路由 (A-STAR)[14]，地理机会路由 (GeOpps)[15] 和基于移动网关的转发 (MGF)[16] 是几种具有固定轨迹的模型。A‐STAR模型中的车辆节点会选择高连通性的路线，这可能导致负载过重甚至拥塞。GeOpps可通过导航系统获取车辆节点的固定轨迹，并利用轨迹信息有选择地将数据包发送给靠近目的节点的车辆。但由于对轨迹过度依赖，其应用受限于导航系统和驾驶员的驾驶习惯。MGF仅使用公交车进行数据传输，因此只能在公交车上使用。不同于上述模型，基于轨迹的数据转发 (TBD)[17]，基于轨迹的统计转发 (TSF)[18]，基于共享轨迹的数据转发方案 (STDFS)[19]，轨迹改善数据传输在车载网络中的应用 (Trajectory)[20] 和延迟最优数据转发 (OVDF)[21] 是几种具有轨迹预测能力的模型。然而，TBD和TSF仅适用于某些特定场景。STDFS由于对轨迹过度依赖而可靠性不高。OVDF也借助公交车的固定轨迹来辅助数据传输。Trajectory模型采用马尔可夫链进行轨迹预测，是一种高效的模型。

最后，基于路侧单元（RSU）的模型是车载网络中数据传输的另一种方案类型，包括上述的TBD、TSF、MGF、SADV、STDFS、OVDF模型。ROAMER[22] 进一步利用RSU并通过依赖有线骨干网络来传输数据，这与车载自组织网络通过车辆节点传输数据的概念相违背，且该模型对RSU有较高的要求。

总之，存在两个问题：（1）基于车辆轨迹先验知识假设的数据转发模型难以适应实际应用中变化的车辆轨迹；（2）而基于广播网络的方法在获取目标车辆位置时会产生较大的网络开销。受已有工作的启发，我们提出了一种基于关联状态的最优数据转发模型（ASODF）来解决上述问题。我们的模型是一种混合模型，包含车对基础设施（V2I）和车对车（V2V）数据传输。

2 背景

2.1 马尔可夫决策过程

马尔可夫决策过程（MDP）是基于马尔可夫过程理论的随机动力系统中的最优决策过程。它被广泛用于求解在各个阶段都需要做出最优决策的序列问题[23]。一个环境动态已知的序列决策问题通常被形式化为一个MDP，其由五元组 〈S, A, T, R, γ〉表征，其中 S是状态集合且非空，A是动作集合且也非空，T: S× A → Π(S) 是转移函数，它给出智能体在状态 s ∈ S执行动作 a ∈ A后转移到下一状态的概率，其中Π(S)表示在 S上的概率分布集合，R表示奖励函数，它给出智能体在状态 st ∈ S执行动作 at ∈ A并转移到状态 st+1 ∈ S时所获得的即时奖励，此时奖励为Rt= R(st, at, st+1)，γ是用于计算期望奖励的折扣因子。MDP基于马尔可夫性质，即无后效性。这意味着转移函数 T(st, at, st+1) 仅依赖于当前状态，而与过去其他状态无关，即 T(st, at, st+1) = P(st+1|st, at)。

求解一个MDP问题的目标是获得一个最优策略 π，该策略为智能体在每个状态下提供最佳决策，从而使智能体最终获得最多的奖励。

当智能体的初始状态为 s0时，智能体会选择并执行动作 a0，随后环境将转移到下一个状态 s1，智能体将继续选择并执行动作，直到达到终止状态。通过迭代收敛后，模型将给出一个最优策略 π。该策略给出了每个状态下的最优动作，即 a= π(s)。

价值函数常用于评估策略。价值函数也被称为累积折扣奖励，它给出了智能体从当前状态 st开始最终所能获得奖励的估计值，即

$$
Vπ(st)= Eπ[R(st)+ γR(st+1)+ γ2R(st+ 2)+ ···] \quad (1)
$$

我们可以根据贝尔曼方程轻松地将其转化为一个简单形式。

$$
Vπ (st)= R(st, at, st+1)+ γ∑p(st+1|st, at)V π (st+1) \quad (2)
$$

最优策略应是能够从每个状态获得最大累积奖励的策略。因此，每个状态 si的最大奖励为：

$$
V ∗ (si)= R(si, ai, sj) + max π ∑_{j∈ S} p(sj|si, ai)V ∗ (sj) \quad (3)
$$

MDP 假设智能体可以获得环境的真实状态，即 s_agent = s_env。

因此，从状态 si到终止状态的最优策略是：

$$
π∗(si)= arg max ai ∑ p(sj|si, ai)V(sj) \quad (4)
$$

求解MDP以获得最优解的方法包括值迭代、策略迭代以及其他线性规划方法。在本文中，我们将使用值迭代方法来求解MDP问题。值迭代的过程见文献 [24]。

2.2 道路上的数据传输

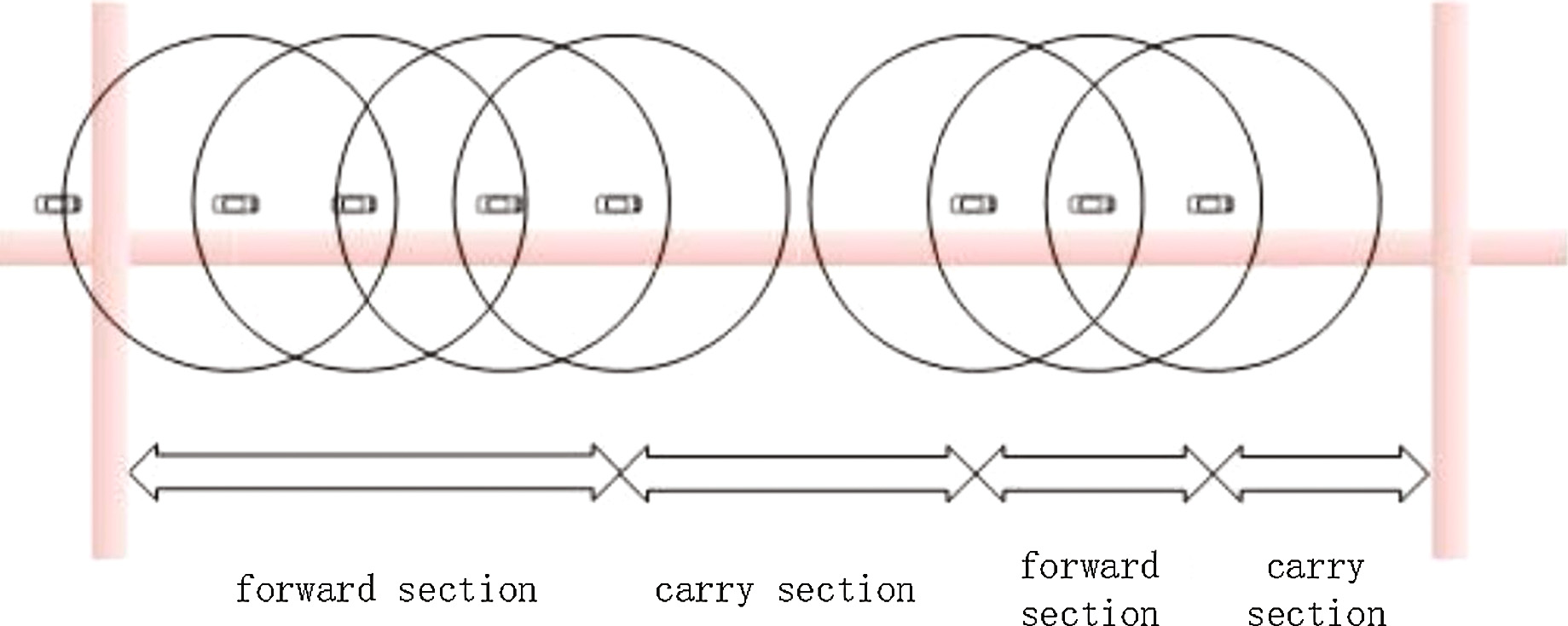
携带转发机制是一种克服车载自组织网络链路频繁断连缺点的有效方法，广泛应用于车载网络的数据传输研究中。道路上数据传输模型的携带转发机制如图1所示。当存在可通信范围内的携带数据车辆，且该车辆比当前车辆更接近下一个交叉口时，则选择并将这些数据传递给距离下一个交叉口最近的车辆。若无此类车辆，则当前车辆将继续携带数据。这是一种贪婪模型，即选择当前情况下的最佳车辆，使数据包能以最快速度和最少转发次数被传送到下一个交叉口。

由于传输过程由车辆存储和无线转发组成，因此数据传输的延迟受两个因素影响：一是车辆密度，二是车辆无线设备通信范围。借鉴文献[13]，我们用 ρij 表示道路密度 eij，R表示无线通信范围半径。VADD假设两车之间距离的分布满足参数为 1/ρij的指数分布。因此，道路上的延迟 dij为 eij：

$$
dij = (1 − e^{−R·ρij}) \frac{lij}{c} + e^{−R·ρij} \frac{lij}{vij} \quad (5)
$$

其中lij 表示道路 eij 的距离，c表示将数据传送到下一跳所需时间，vij 表示道路 eij 上的平均速度。这些参数可通过GPS设备、道路交通统计或对历史轨迹数据的分析获得。

2.3 捉人游戏的关联状态

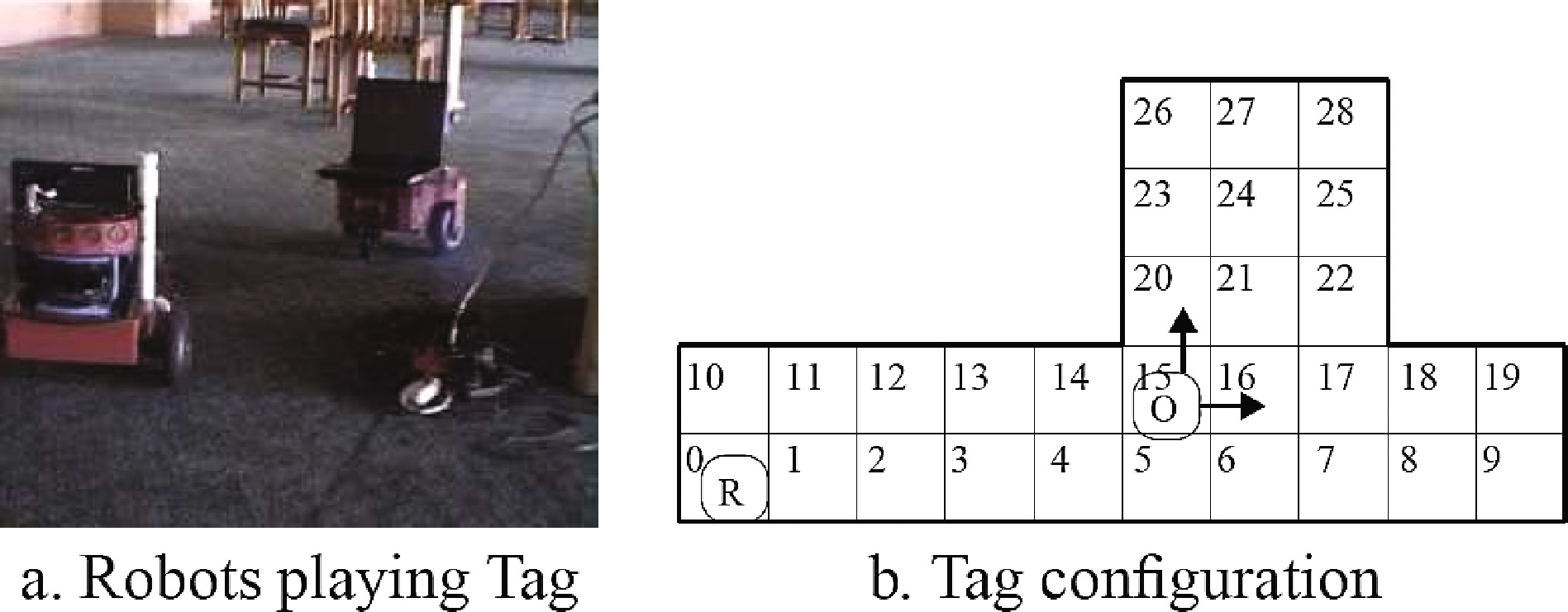
与现有的MDP在数据传输中的应用不同，本文中使用的MDP的状态是通过捕捉游戏学习得到的关联状态。捕捉游戏中有两个角色：机器人和对手，其过程是机器人持续追逐对手直至机器人追上对手，如图2所示。

Tag游戏可以被视为一个部分可观测马尔可夫决策过程任务，其中状态由机器人和对手的位置组成，即关联状态。机器人的状态集合为{s0,···, s29}，对手的状态集合为{s0,···, s29, stagged}，关联状态为 s={Robot, Opponent}。机器人将执行动作集合 North, South, West, East, Tag中的一个动作，然后获得即时奖励。当机器人与对手处于同一个格子中，即 Opponent= stagged时，机器人将捕捉对手并获得最高奖励，游戏结束。

3 基于关联状态的数据转发模型

MDP 已被广泛用于解决序列决策任务。由于携带数据的车辆会以不同概率遇到其他车辆，因此车载自组织网络中的数据转发可被建模为一个序列决策问题。我们可以将数据从源节点传输到目的车辆的过程类比为抓捕游戏中的机器人追逐对手，即数据包追逐目的车辆，且携带数据的车辆不断变化。在本节中，我们将该问题建模为一个马尔可夫决策过程任务。

3.1 关联状态

关联状态是动态获取目的车辆位置并优化转发数据的核心。通过使用关联状态，我们可以将目的车辆的位置信息加入MDP模型中，并动态优化数据传输的网络延迟。

在我们的模型中，使用当前交叉口作为当前车辆状态。因此，关联状态由源车辆的交叉口和目的车辆的交叉口组成。当源车辆节点获取到目的车辆节点的交叉口信息时，将利用低负载路侧单元及其有线骨干网辅助通信。我们假设每辆车辆在进入交叉口的路侧单元覆盖区域时，都会向该路侧单元注册信息。一旦路侧单元检测到目的车辆节点，其交叉口信息将通过路侧单元骨干网络传输至距离源车辆节点最近的路侧单元，随后目的车辆节点的位置信息将被发送给源车辆节点，使其获得当前关联状态。由于使用了路侧单元骨干网络，时延可以忽略不计。下一个状态也是求解马尔可夫决策过程问题的必要条件。

在我们的模型中，可以获取目的车辆的速度、位置、方向等信息。通过这些信息，即使当前车辆尚未进入下一个交叉口的覆盖范围，我们也能确定其下一个交叉口。因此，我们可以得到下一个关联状态。

3.2 关联状态的决策

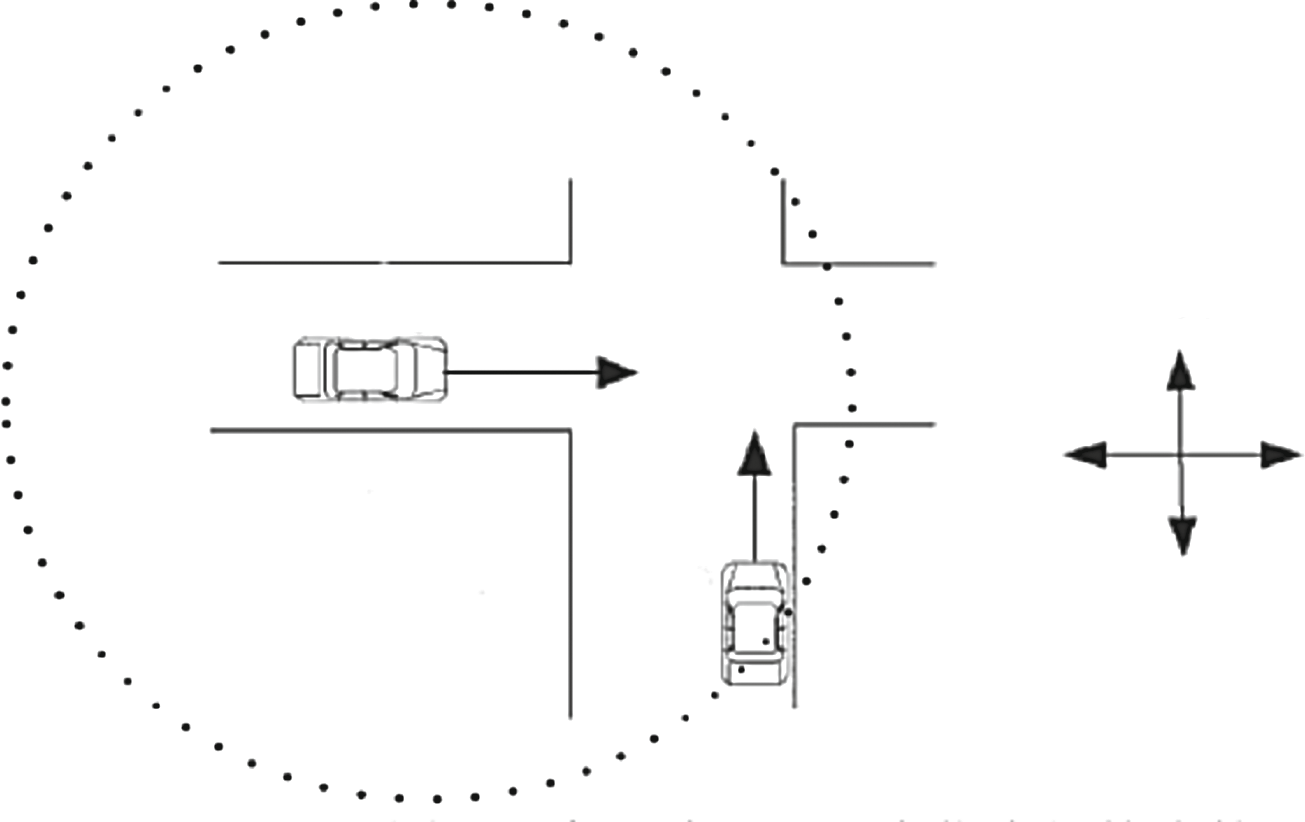
正如我们已经描述了在路段上的传输，接下来将展示在交叉口的数据传输过程。我们将根据固定策略（如VADD）为方向分配优先级，如图3所示，其中1表示传输数据的最佳方向，2表示次优方向，依此类推。我们将选择最优方向，即优先级为1的方向：若该方向有车辆，则向其传输数据；否则检查自身是否正朝该方向行驶，若是，则不向其他车辆转发；若不是，则选择优先级为2的方向的车辆，以此类推。

在交叉口 i，决策（动作）可以表示为向量集合 U(i)，其中 π1 i π 2 i π 3 i ··· πmi i ∈ E 是与交叉口 i 相连的所有 mi 道路路段，且顺序表示优先级。我们的目标是从集合 U(i) 中选择最佳决策（动作），以在当前交叉口传输数据。

3.3 转移概率

我们使用 $P(s, \pi_i, s’)$ 表示转移概率，其中状态 $s$ 由源车辆和目的车辆的交叉路口组成。因此，$P(s, \pi_i, s’)$ 包含两部分：源车辆的转移概率 $P(\text{src} t, \pi_i, \text{src} {t+1})$ 和目的车辆转向下一个交叉口的转移概率 $P(\text{dest}, \text{dest}+1)$。

假设当前交叉口为 $i$，且策略为 $\pi_i$，$P_{ij}(\pi_i) = P(\text{src} t, \pi_i, \text{src} {t+1})$ 表示数据沿道路 $e_{ij}$ 传输到下一个交叉口 $j$ 的概率，其中 $\text{src} t = i, \text{src} {t+1} = j$。

（1）$P(\text{src} t, \pi_i, \text{src} {t+1})$ 的计算。我们定义三个概率事件：

• A 表示一辆车辆尚未遇到前往优先级高于该路段的路段的车辆的事件。
• B 表示一辆车辆在交叉口 $i$ 遇到另一辆驶向道路 $e_{ij}$ 的车辆，且该车辆自身并未驶向一个具有更高优先级方向的道路 $e_{ij}$ 的事件。
• C 表示一辆车辆驶向道路 $e_{ij}$ 的事件。

根据上述定义，我们可以推导出 $P_{ij}(\pi_i)$ 的概率：

$$
p(\text{src} t, \pi_i, \text{src} {t+1}) = P_{ij}(\pi_i) = P[A \cap (B \cup C)] = P(A) \times P(B \cup C) = P(A) \times [P(B) + P(C) - P(B|C)P(C)]
$$

$$
= \left[ \prod_{e_{ik} \in HP_{e_{ij}}(\pi_i)} (1 - p_{ik}) \right] \times \left[ p_{ij} \times \left(1 - \sum_{e_{ik} \in HP_{e_{ij}}(\pi_i)} p’ {ik} \right) + p’ {ij} - p_{ij} \times p’_{ij} \right] \quad (6)
$$

其中，$P(A)$ 表示事件 A 发生的概率，$HP_{e_{ij}}(\pi_i)$ 表示比道路 $e_{ij}$ 具有更高优先级的道路集合。$p_{ij}$ 表示一辆车辆从交叉口 $i$ 行驶到交叉口 $j$ 的概率，$p’ {ij}$ 表示一辆车辆在从交叉口 $i$ 驶向道路 $e {ij}$ 时遇到其他车辆的概率。在我们的模型中，我们设定：

$$
p_{ij} = \frac{#\text{num}(i \to j)}{#\text{num}(i)}
$$

其中 $#\text{num}(i \to j)$ 表示当车辆位于交叉口 $j$ 时前往交叉口 $i$ 的车辆数量，$#\text{num}(i)$ 表示到达交叉口 $i$ 的所有车辆数量。并且我们设定：

$$
p’_{ij} = \frac{#\text{num_met}(i \to j)}{#\text{num_met}(i)}
$$

其中 $#\text{num_met}(i \to j)$ 表示该车辆在交叉口 $i$ 遇到并前往交叉口 $j$ 的车辆数量，$#\text{num_met}(i)$ 表示该车辆在交叉口 $i$ 遇到的所有车辆数量。

（2）转移函数 $T$ 的计算 $P(\text{dest}, \text{dest}+1)$。在我们的模型中，我们设定：

$$
P(\text{dest}, \text{dest}+1) = \frac{#\text{num}(\text{dest} \to \text{dest}+1)}{#\text{num}(\text{dest})}
$$

其中 $#\text{num}(\text{dest} \to \text{dest}+1)$ 表示在时间 $t$ 到达交叉口 $i$ 并在时间 $t+1$ 到达交叉口 $j$ 的车辆数量，$#\text{num}(\text{dest})$ 表示在时间 $t$ 到达交叉口 $i$ 的所有车辆的数量。

因此，一辆载车在时间 $t$ 到达交叉口 $i$ 时的完整关联状态转移概率 $P(s, \pi_i, s’)$ 为：

$$
P(s, \pi_i, s’) = P(s_{t+1} = s | a_t = \pi, s_t = s’) = P((\text{src}, \text{dest}) {t+1} | \pi_i, (\text{src}, \text{dest})_t) = P(\text{src}_t, \pi_i, \text{src} {t+1}) \ast P(\text{dest}, \text{dest}+1) = P_{ij}(\pi_i) \ast P(\text{dest}, \text{dest}+1) \quad (7)
$$

3.4 模型推导

网络时延是车载自组织网络性能的重要指标。其值为数据包经过的道路上延迟的累积，对应于马尔可夫决策过程中的价值函数构成。因此，我们将时延作为马尔可夫决策过程的奖励。

假设在状态 $s$ 存在四个相邻状态，则从状态 $s$ 的转移模型如图4所示。其中，$D_s(\pi)$ 表示从状态 $s$ 的价值函数，即处于状态 $s$ 的源车辆的估计总时延。因此，$D_s(\pi)$ 可表示为：

$$
D_s(\pi_s) = \sum_{s’ \in N(s)} P(s, \pi_s, s’) \times [R(s, \pi_s, s’) + D’_s(\pi)] \quad (8)
$$

$$
= P_{s,s1} \times (R(s, \pi_s, s1) + D_{s1}(\pi_s)) + P_{s,s2} \times (R(s, \pi_s, s2) + D_{s2}(\pi_s)) + P_{s,s3} \times (R(s, \pi_s, s3) + D_{s3}(\pi_s)) + P_{s,s4} \times (R(s, \pi_s, s4) + D_{s4}(\pi_s)) \quad (9)
$$

我们的目标是最小化总时延，即

$$
\min_\pi D_s(\pi), \quad \forall s \quad (10)
$$

我们将得到的最优策略是：

$$
\pi^ = \langle \pi^ _s, \forall s \in S \rangle \quad (11)
$$

我们获得的奖励 $R(s, \pi_i, s’)$ 推导如下：

$$
R(s, \pi_i, s’) = R((\text{src} t, \text{dest}), \pi_i, (\text{src} {t+1}, \text{dest}+1)) \quad (12)
$$

$$
= \frac{1}{2}(d_{\text{src} {t+1},\text{src}_t} + d {\text{dest}+1,\text{dest}}) \quad (13)
$$

3.5 算法

由于我们的模型仍然是一个标准的 MDP 模型，我们可以使用标准的值迭代来解决这个问题。该算法如算法1所示。

算法 1. ASODF：基于关联状态的最优数据转发模型

输入：初始化所有状态的值为 $D_0$，最大迭代次数 $\tau$ 和阈值 $\theta$。
输出：最优策略 $\pi^ = \langle \pi^ _s, \forall s \in S \rangle$ 和相应的期望时延 $D^ (\pi^ )$

1: 初始化 $g_0 = 0$ 和 $d_0 = 0$；局部：$k = 0$
2: 重复
3: $D^{k+1} s = \sum {s’ \in N(s)} T(s, \pi_s, s’) \times (d_{s,s’} + D^{k+1} {s’})$
4: $\pi^{k+1}_s = \arg\min {\pi_s \in \cap(s)} \sum_{s’ \in N(s)} T(s, \pi_s, s’) \times (d_{s,s’} + D^k_{s’})$
5: $k = k + 1$
6: 直到 $\max_{s \in S} |D^k_s - D^{k-1}_s| < \theta$ 或 $k > \tau$
7: $\pi^ _s = \pi^ _s, \pi^ = \langle \pi^ _s, \forall s \in S \rangle$
8: 返回 $\pi^ , D^ _s(\pi^*)$

4 实验

4.1 数据集

为了使实验结果更加真实和有说服力，我们在上海 SUVnet 的真实车辆数据集上运行实验[26]。它包含 5000 辆出租车和公交车的轨迹数据，我们仅使用其中出租车的数据。我们对数据集进行了预处理，包括：

• 数据清洗，包括去除重复数据和错误数据。
• 基于道路结构修复漂移数据。
• 由于出租车数据平均每 30 秒记录一次，我们对不连续轨迹数据和错误轨迹数据进行了插值处理。

4.2 实验设置

我们选取约 2700 辆出租车作为目标车辆。在实验中，我们随机选择 200 辆车作为源车辆和目的车辆来传输数据。我们假设每个数据包大小相同。一些超参数如表1所示。

表1. 实验的参数设置

参数	值（范围）
无线传输范围	200 米
实验车辆数量	300 到 2700
θ	0.001
τ	1000
携带数据的车辆数量	200
到下一个路口的时间差	10秒
生存时间（TTL）	1 h, 2 h, 3 h

4.3 实验结果分析

我们将我们的模型 ASODF 与 OVDF-P 进行了比较，OVDF-P 是 OVDF 的模型之一。在 OVDF 中，当数据包被传输到路侧单元时即视为成功传输，我们更改了这一设置。在我们的实验中，当数据包被传输到移动车辆时，即视为传输成功。平均投递率和平均延迟的结果分别如图5(a)和(b)所示。

图5(a) 的结果表明，当车辆数量相同时（即车辆密度相同），我们的模型具有较高的投递率。一个明显的结论是，随着车辆数量的增加，两个模型的平均投递率都会提高。图5(b) 显示，当车辆数量较少时，即网络中车辆稀疏时，我们的模型延迟较低，表现更优；并且随着车辆数量的增加，两个模型的延迟表现将趋于相似。

(a) 平均投递率结果
(b) 平均延迟结果
图5。 POMDP 到 MDP 的泛化性能

表2。平均投递率比较

车辆数量	ASODF	OVDF	提升
300	0.52	0.47	10.64%
600	0.61	0.56	8.93%
900	0.69	0.63	9.52%
1200	0.78	0.73	6.85%
1500	0.83	0.79	5.06%
1800	0.87	0.85	2.35%
2100	0.90	0.88	2.27%
2400	0.91	0.89	2.25%
2700	0.92	0.90	2.22%

表3. 平均延迟对比

车辆数量	ASODF (s)	OVDF (s)	提升
300	250	290	13.79%
600	230	250	8.71%
900	200	220	9.09%
1200	140	170	17.65%
1500	120	145	17.24%
1800	100	110	9.10%
2100	90	95	5.26%
2400	88	90	2.52%
2700	86	89	3.37%

两种模型的比较结果如表2和表3所示。表2显示，随着车辆数量的增加，我们的模型相较于 OVDF 的提升趋于一个较小的值，即 2.22%。原因是随着车辆密度的增加，车辆通信链路断开的情况越来越少，越来越多的数据包通过无线方式传输，因此提升幅度逐渐减小。而表3显示，在低车辆密度下，平均延迟的提升为 13.79%。综上所述，我们的模型优于 OVDF，特别是在低车辆密度情况下。

5 结论

本文中，我们提出了一种基于关联状态的最优数据转发模型（ASODF），以提高车载自组织网络（VANET）中的数据投递率并降低投递延迟。我们的模型将数据转发问题建模为强化学习任务，并采用标准的值迭代方法进行求解。实验表明，该模型能够获得较高的投递率和较低的延迟，特别是在处理 VANET 稀疏环境时表现更优。