旅行【图论】【堆】

>Description

---

>Input

>Output

---

>Sample Input
5 6
1 2 3
1 3 4
2 4 2
2 5 3

>Sample Output
4

---

>解题思路
由题意得，此无向图可以看做成一棵树，如：

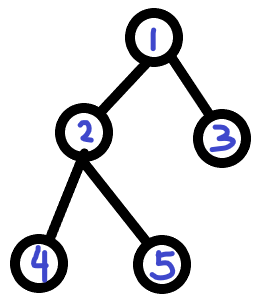
求某两点的最短路代价，通过推算得出（题目中的加加减减），a ~ b = a ~ 1(根节点) + 1 ~ b，并且第一个符号与最后一个符号肯定都为加
因为题目要求的路径的条数必须为奇数，所以符合条件的路径必须是从偶数层出发到达奇数层的（也可以反过来，不过都一样），所以我们可以对1~任何点的代价做一个预处理（注意处理到任何点的最后一个符号为+，这里可以统一处理，最后不符合的取相反数），把它们分为偶数层出发disa和奇数层出发disb两个数组，分别从小到大排个序，disa+disb维护一个小根堆（这里用到两个指针分别指向两个数组），第k个弹出的就是答案。

---

>代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;

struct ooo
{
	ll to, next, c;
} a[200005];
struct ooo2
{
	ll c, h; //堆数组，c记录数据，h记录这个节点指向的disa的位置
} d[500005];
ll n, k, x, y, z, t, dep[100005], h[100005], f[100005];
ll disa[100005], disb[100005], u[100005];

void dfs (ll s, ll fath, ll p) //s当前节点，fath为s的父亲，p记录符号
{
	dep[s] = dep[fath] + 1; //计算深度
	for (ll i = h[s]; i; i = a[i].next)
	  if (a[i].to != fath)
	  {
	  	f[a[i].to] = f[s] + p * a[i].c; //dp计算1~i的代价
	  	dfs (a[i].to, s, -p); //要变符号
	  }
}

void swapp (ll aa, ll bb)
{
	ll tt;
	tt = d[aa].c, d[aa].c = d[bb].c, d[bb].c = tt;
	tt = d[aa].h, d[aa].h = d[bb].h, d[bb].h = tt;
} //交换

void up (ll s)
{
	while (s / 2 != 0 && d[s / 2].c > d[s].c)
	{
		swapp (s / 2, s);
		s = s / 2;
	}
}

void down (ll s)
{
	while ((d[s * 2].c != d[0].c && d[s].c > d[s * 2].c) 
	     || (d[s * 2 + 1].c != d[0].c && d[s].c > d[s * 2 + 1].c))
	{
		ll l = s * 2;
		if (d[s * 2 + 1].c < d[s * 2].c) l++;
		swapp (s, l);
		s = l;
	}
} 

int main()
{
	scanf ("%I64d%I64d", &n, &k);
	for (ll i = 1; i < n; i++)
	{
		scanf ("%I64d%I64d%I64d", &x, &y, &z);
		a[++t].to = y;  a[t].next = h[x];  a[t].c = z;  h[x] = t;
		a[++t].to = x;  a[t].next = h[y];  a[t].c = z;  h[y] = t;
	}
	dep[0] = -1; //我用的是1为根节点，深度为0
	dfs (1, 0, 1);
	disa[++disa[0]] = 0; //注意a也可以为树的根节点，此时距离为0
	for (ll i = 2; i <= n; i++)
	  if (dep[i] % 2 == 0) disa[++disa[0]] = -f[i]; //处理：使偶数层最后的符号也为+
	  else disb[++disb[0]] = f[i];
	sort (disa + 1, disa + 1 + disa[0]);
	sort (disb + 1, disb + 1 + disb[0]); //排序
	t = disa[0]; //t记录小根堆的大小
	
	for (ll i = 0; i < 500005; i++) d[i].c = 9223372036854775807; //longlong上线
	for (ll i = 1; i <= t; i++) u[i] = 1, d[i].c = disa[i] + disb[1], d[i].h = i; //加入堆
	                            //u[i]记录disa[i]现在指向的disb的位置
	for (ll i = 2; i <= t; i++) up(i); //建堆
	for (ll i = 1; i <= k; i++)
	{
		if (i == k)
		{
			if (t <= 0) printf ("Stupid Mike"); //不知道为什么在学校oj上交的这个点是错的但是好像没有什么毛病TT
		    else printf ("%I64d", d[1].c);
		}
		if (u[d[1].h] + 1 <= disb[0]) d[1].c = disa[d[1].h] + disb[++u[d[1].h]]; //如果还有匹配的disb
		else 
		{
			swapp (1, t);
			d[t].c = d[0].c, d[t].h = 0;
			t--; //如果没有了的话就去掉一个点
		}
		down(1);
	}
	return 0;
}