数据结构——图论

hello-hebin

已于 2022-05-31 15:25:31 修改

阅读量882

点赞数

分类专栏： # 数据结构与算法文章标签：图论数据结构深度优先

于 2022-05-23 14:32:30 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_44505194/article/details/124685051

版权

数据结构与算法专栏收录该内容

8 篇文章

订阅专栏

本文介绍了图论中的单源最短路径算法，包括弱化版和标准版，以及图的遍历方法，如深度优先搜索和广度优先搜索。此外，还涵盖了各种实际问题的应用，如查找文献、网络设计等，展示了图论在解决实际问题中的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

前 4 题为洛谷题目

P3371 【模板】单源最短路径（弱化版）

【题目背景】
本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

【题目描述】
如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

【输入格式】
第一行包含三个整数 $n, m, s$ ，分别表示点的个数、有向边的个数、出发点的编号。

接下来 $m$ 行每行包含三个整数 $u, v, w$ ，表示一条 $\to v$ 的，长度为 $w$ 的边。

【输出格式】
输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$ 。

【样例输入 #1】

【样例输出 #1】

0 2 4 3

【数据范围】
对于 $20\%$ 的数据： $1\le n \le 5$ ， $1\le m \le 15$ ；
对于 $40\%$ 的数据： $1\le n \le 100$ ， $1\le m \le 10^4$ ；
对于 $70\%$ 的数据： $1\le n \le 1000$ ， $1\le m \le 10^5$ ；
对于 $100\%$ 的数据： $\le n \le 10^4$ ， $1\le m \le 5\times 10^5$ ， $1\le u,v\le n$ ， $w\ge 0$ ， $\sum w< 2^{31}$ ，保证数据随机。

对于真正 $100\%$ 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

图片1到3和1到4的文字位置调换

参考程序

#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,m,s,dis[N], vis[N];
struct T{
    int v,w;
};
vector<T> G[N];
void add(int u, int v, int w){
    T temp;
    temp.v = v;
    temp.w = w;
    G[u].push_back(temp);
}
void add2(int u, int v, int w){
    add(u, v, w), add(v, u, w);
}
void print(){//图的打印 
    for(int i=1; i<=n; i++){
        cout<<i<<" : ";
        for(int j=0; j<G[i].size(); j++){
            cout<<G[i][j].v<<" "<<G[i][j].w<<"; ";
        }cout<<endl;
    }
}
void dijkstra(int s){
    fill(dis, dis+N, INT_MAX);   //将 dis初始化为 INT_MAX 
//    memset(dis, 0x7f, sizeof(dis));//将 dis的每个字节位都初始化为 0x3f, vis[i]=0x3f3f3f3f
    memset(vis, 0, sizeof(vis));   //将 vis初始化为 0
    dis[s]=0;
    for(int i=1; i<=n; i++){
        int minn=INT_MAX, u=0;   //定义 u为当前未处理的最小路径所在节点 
        for(int j=1; j<=n; j++){ //这里一步，如果使用链式向前星会发生变化 
            if(minn>dis[j] && !vis[j]){
                minn=dis[j], u=j;
            }
        }
//        if(u==0) break;
        vis[u]=1;
        for(int j=0; j<G[u].size(); j++){
            T temp = G[u][j];
            int v = temp.v, w=temp.w;
            if(dis[u]+w < dis[v]){
                dis[v] = dis[u]+w;
            }
        }
    }
}
int main(){
//    freopen("data.in", "r", stdin); 
    cin>>n>>m>>s;
    for(int i=1; i<=m; i++){
        int u, v, w; cin>>u>>v>>w;
        add(u, v, w);
    }
//    print();
    dijkstra(s);
    for(int i=1; i<=n; i++) cout<<dis[i]<<" ";
	return 0;
}

P4779 【模板】单源最短路径（标准版）

【题目背景】

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程一题里非常熟练地使用了一个广为人知的算法求最短路。然后呢？ $\rightarrow 60$ ； $\text{Ag} \rightarrow \text{Cu}$ ；

最终，他因此没能与理想的大学达成契约。小 F 衷心祝愿大家不再重蹈覆辙。

【题目描述】

给定一个 $n$ 个点， $m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。

数据保证你能从 $s$ 出发到任意点。

【输入格式】

第一行为三个正整数 $n, m, s$ 。
第二行起 $m$ 行，每行三个非负整数 $u_i, v_i, w_i$ ，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

【输出格式】

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的距离。

【样例输入 #1】

【样例输出 #1】

0 2 4 3

【提示】

样例解释请参考数据随机的模板题。

$\leq n \leq 10^5$ ；

$\leq m \leq 2\times 10^5$ ；

$s = 1$ ；

$\leq u_i, v_i\leq n$ ；

$\leq w_i \leq 10 ^ 9$ ,

$\leq \sum w_i \leq 10 ^ 9$ 。

参考程序

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+1;
const int INF=(1<<31)-1;
int n,m,s,dis[N],vis[N];
struct T{
    int v,w;
};
bool operator< (T a, T b) {
    return a.w>b.w;
}
struct cmp{
    bool operator() (const T a, const T b) const {
        return a.w>b.w;
    }
};
vector<T> G[N];
//基于vector邻接表建图
void add(int u, int v, int w){
    G[u].push_back((T){v,w});
}
void add2(int u, int v, int w){
    add(u, v, w), add(v, u, w);
}
void print(){//图的打印 
    for(int i=1; i<=n; i++){
        cout<<i<<" : ";
        for(int j=0; j<G[i].size(); j++){
            cout<<G[i][j].v<<" "<<G[i][j].w<<"; "; 
        }cout<<endl;
    }
}
//朴素算法 
void dijkstra(int s){
    fill(dis, dis+N, INT_MAX);//将dis全部初始化为INT_MAX
//  memset(dis, 0x7f, sizeof(dis));//将dis每个Byte都初始化为0x7f,vis[i]=0x7f7f7f7f,取不到INT_MAX
    memset(vis, 0, sizeof(vis));//将 vis初始化为 0
    dis[s]=0;
    for(int i=s; i<=n; i++){
        int minn=INT_MAX, u=0;//定义u为当前未处理的最小路径所在节点
        for(int j=1; j<=n; j++){
            if(!vis[j] && dis[j]<minn){
                minn=dis[j], u=j;
            }
        }
        if(u==0) break;//源点到其它点没有路径，就不用遍历了呀，机智
        vis[u]=1;
        for(int j=0; j<G[i].size(); j++){
            int v=G[i][j].v, w=G[i][j].w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
            }
        }
    }
}
//堆优化 - 加速
void dijkstra2(int s){
    fill(dis, dis+N, INT_MAX);
    memset(vis, 0, sizeof(vis));
    dis[s]=0;
    priority_queue<T> pq;
//    priority_queue<T, vector<T>, cmp> pq; 
    pq.push((T){s, 0}); //按照定义先后对应终点与权值
    while(!pq.empty()){
        T temp=pq.top(); pq.pop();
        int u=temp.v;
        if(vis[u]) continue;//源点已访问 
        vis[u]=1;
        for(int i=0; i<G[u].size(); i++){
            T temp=G[u][i];
            int v=temp.v, w=temp.w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                if(vis[v]==0) pq.push((T){v,dis[v]});
            }
        }
    }
}
int main(){
//    freopen("data.in", "r", stdin);
    cin>>n>>m>>s;
    for(int i=1; i<=m; i++){
        int u,v,w; cin>>u>>v>>w; add(u, v, w);
    }
//    print();
//    dijkstra(s);
    dijkstra2(s);
    for(int i=1; i<=n; i++) cout<<dis[i]<<" ";
    return 0;
}

P3916 图的遍历

【题目描述】

给出 $N$ 个点， $M$ 条边的有向图，对于每个点 $v$ ，求 $A (v)$ 表示从点 $v$ 出发，能到达的编号最大的点。

【输入格式】
第1 行，2 个整数 $N, M$ 。

接下来 $M$ 行，每行2个整数 $U_i,V_i$ ，表示边 $U_i,V_i)$ 。点用 $2,\cdots,N$ 编号。

【输出格式】
N 个整数 $A(1),A(2),\cdots,A(N)$ 。

【样例输入 #1】

【样例输出 #1】

4 4 3 4

【提示】
对于60% 的数据， $\le N . M \le 10^3$ ；
对于100% 的数据， $\le N , M \le 10^5$ 。

参考程序

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+1;
vector<int> G[N];
int n,m,Max[N];//Max[i]表示始于i点的最大节点，先初始化为0

//dfs(起点，终点)
void dfs(int s, int e){
    if(Max[s]) return;//访问过最大值了，没必要继续访问
    Max[s]=e;
    for(int i=0; i<G[s].size(); i++){
        dfs(G[s][i], e);
    }
}

int main(){
    ios::sync_with_stdio(false);
    //freopen("data.in", "r", stdin);
    cin>>n>>m;
    for(int i=1; i<=m; i++) {
        int u,v; cin>>u>>v;
        G[v].push_back(u);//反向建边：考虑较大的点可以到达那些点
    }
    for(int i=n; i>=1; i--) dfs(i,i);//逆序处理快
    for(int i=1; i<=n; i++) cout<<Max[i]<<" ";
    return 0;
}

P5318 【深基18.例3】查找文献

【题目描述】

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$ ）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

【输入格式】
共 $m + 1$ 行，第 1 行为 2 个数， $n$ 和 $m$ ，分别表示一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$ ）以及 $m(m\le10^6)$ 条参考文献引用关系。

接下来 $m$ 行，每行有两个整数 $X, Y$ 表示文章 X 有参考文献 Y。

【输出格式】
共 2 行。
第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

【样例输入 #1】

【样例输出 #1】

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

参考程序

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+1;
int n,m, cnt=0;
int vis[N];// 0表示未看过，1表示看过 

//邻接表
vector<int> G[N];
void add(int u, int v){
    G[u].push_back(v);
}

//dfs(当前文献) 
void dfs1(int x){
    cout<<x<<" "; vis[x]=1;
    for(int i=0; i<G[x].size(); i++){
        if(!vis[G[x][i]]) dfs1(G[x][i]);
    } 
}

//bfs(当前文献)
void bfs1(int x){
    memset(vis, 0, sizeof(vis));
    cout<<x<<" ";
    for(int i=x; i<=n; i++){
        for(int j=0; j<G[i].size(); j++){
            if(vis[G[i][j]]==0){
                cout<<G[i][j]<<" ";
                vis[G[i][j]]=1;            
            } 
        }
    }
}

void bfs2(int x){
    memset(vis, 0, sizeof(vis));
    queue<int> que;
    que.push(x); cout<<x<<" "; vis[x]=1;
    while(!que.empty()){
        int a = que.front(); que.pop();
        for(int i=0; i<G[a].size(); i++){
            int p=G[a][i];
            if(!vis[p]) {
                cout<<p<<" ";
                vis[p]=1;
                que.push(p);
            }
        }
    }
}

/
//链式向前星
//struct T{
//    int to;
//    int next;
//}edge[N];
//int head[N];
//
//void add2(int u, int v){
//    edge[cnt].to = v;
//    edge[cnt].next = head[u];
//    head[u] = cnt++;
//} 

int main(){
    ios::sync_with_stdio(false);
//    freopen("data.in", "r", stdin);
//    freopen("data2.in", "w", stdout);
    cin>>n>>m;
    for(int i=1; i<=m; i++){
        int u,v; cin>>u>>v;
        add(u,v);
    }    
    for(int i=1; i<=n; i++) sort(G[i].begin(), G[i].end());
    dfs1(1); cout<<endl;
    bfs2(1); 
    return 0;
}

图论入门计蒜客 - T1325

问题描述

假设用一个 n×n 的数组 a 来描述一个有向图的邻接矩阵：

（1）编写一个函数确定一个顶点的出度
（2）编写一个函数确定一个顶点的入度
（3）编写一个函数确定图中边的数目

输入格式

第一行：节点总数 n、指定节点 m；下面 n 行：有向图的邻接矩阵

输出格式

第一行包括三个数据：节点编号 m、m 的出度、m的入度（之间用一个空格隔开）。
第二行包括一个数据：图中边的总数。

数据范围：1≤n, m, a[i][j]≤1000。

输入样例：

输出样例：

3 2 3
15

参考程序

#include<iostream>
using namespace std;
const int N=1e3+10;
int a[N][N];
int n,m; 
int in_degree(int j){
    int ans=0;
    for(int i=1; i<=n; i++){
        if(a[i][j]!=0) ans++;
    }
    return ans;
}
int out_degree(int i){
    int ans=0;
    for(int j=1; j<=n; j++){
        if(a[i][j]!=0) ans++;
    }
    return ans;
}
int number_sides(){
    int ans=0;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            if(a[i][j]!=0) ans++;
        }
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            cin>>a[i][j]; 
        }
    }
    cout<<m<<" "<<out_degree(m)<<" "<<in_degree(m)<<endl<<number_sides()<<endl;
    return 0;
}

p节点计蒜客 - T1421

问题描述

给出一颗有根树，总共 n 个节点，
如果一个节点的度不小于它所有的儿子以及他的父亲的度（如果存在父亲或者儿子），
那么我们称这个点为 p 节点，现在给你一棵树你需要统计出 p 节点的个数。

这里的度数指树上的度数，即一个节点的子节点数。

输入格式

输入的第一行包含一个整数 t（1≤t≤100），表示数据组数。
接下来 t 组数据，每组数据第一行一个数 n（1≤n≤1000），表示树的节点数。
然后 n-1 行，每行两个数 x，y（0<x,y<n），代表 y 是 x 的儿子节点。

输出格式

输出 t 行，每一行一个整数，代表 p 节点的个数。

输入样例

输出样例：1

参考程序


#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
const int N=1e5+10;
int f[N]; // f[i] 表示 i的父节点
vector<int> G[N];
int main_ac() {
//    freopen("data.in","r",stdin);
    ios::sync_with_stdio(false);
    int t; cin>>t;
    while(t--) {
        memset(f, 0, sizeof(f));//多组数据，要初始化
        for(int i=1; i<N; i++) G[i].clear();
        int n,x,y; cin>>n;
        for(int i=1; i<n; i++) {
            cin>>x>>y; G[x].push_back(y);
            f[y] = x;  // y 的父亲是 x 
        }
        int ans=0;
        for(int i=1; i<=n; i++) {
            bool flag=1;
            if(G[i].size()<G[f[i]].size()) continue;// 不小于父亲的度
            for(int j=0; j<G[i].size(); j++) {      // 不小于所有儿子的度
                if(G[i].size()<G[G[i][j]].size()) flag = 0;
            }
            if(flag) ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}
bool vis[N];
int main() {   // 打标记的写法
//    freopen("data.in","r",stdin);
    ios::sync_with_stdio(false);
    int t; cin>>t;
    while(t--) {
        memset(f, 0, sizeof(f));//多组数据，要初始化
        memset(vis, 0, sizeof(vis));
        for(int i=1; i<N; i++) G[i].clear();
        int n,x,y;  cin>>n;
        for(int i=1; i<n; i++) {
            cin>>x>>y; G[x].push_back(y);
            f[y] = x; // y 的父亲是 x
        }
        int ans=0;
        for(int i=1; i<=n; i++) {
            if(f[i]!=0 && G[i].size() < G[f[i]].size()) vis[i]=1; // 不小于父亲的度
            for(int j=0; j<G[i].size(); j++) {                    // 不小于所有儿子的度
                if(G[i].size() < G[G[i][j]].size()) vis[i]=1;     
            }
        }
        for(int i=1; i<=n; i++) if(!vis[i]) ans++;
        cout<<ans<<endl;
    }
    return 0;
}

参考程序：邻接矩阵

#include<iostream>
#include<cstring>
using namespace std;
const int N=1010;
int a[N][N],b[N],c[N],f[N];
int main() {
//	freopen("data.in", "r", stdin);
    int t; cin>>t;
    while(t--) {
        memset(a, 0, sizeof(a));  memset(b, 0, sizeof(b));
        memset(c, 0, sizeof(c));  memset(f, 0, sizeof(f));
        int n,ans=0; cin>>n;
        for(int i=1; i<n; i++) {
            int x,y; cin>>x>>y;
            a[x][y]=1; // x 是 y 的父亲
        }
        for(int i=1; i<=n; i++) f[i]=i;
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) {
                if(a[i][j]!=0) {
                    f[j]=i;  // j 的父节点为i
                    b[i]++;  // i 的出度
                }
            }
        }
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) {
                if(f[i]!=0 && b[i]<b[f[i]]) c[i]=-1;// 不小于父亲的度
                if(a[i][j]!=0 && b[i]<b[j]) c[i]=-1;// 不小于所有儿子的度
            }
        }
        for(int i=1; i<=n; i++) if(c[i]!=-1) ans++;
        cout<<ans<<endl;
    }
    return 0;
}

A Knight’s Journey POJ - 2488

问题描述

整天待在一个方块里, 骑士感到特别的无聊, 于是, 他决定来一场所走就走的旅行
但他只能走日字, 并且世界是一个不大于 8*8 的棋盘.你能帮勇敢的骑士制定一个旅行计划吗?
请找出一条路使得骑士能够走遍整个棋盘.骑士可以在任一方块出发或结束。

输入格式

第一行输入一个正整数n, 代表数据组数
对于每组数据, 含有两个正整数 p 和 q (1 <= p*q <= 26), 表示一个 p*q 的棋盘.
每个方块的位置用两个字符表示, 第一个从A开始,代表列, 第二个从1开始,代表行。

输出格式

每组数据的结果首先是一行"Scenario #i:“, i是数据序号, 从1开始
然后输出一行, 是字典序第一的可以走遍棋盘的路径, 接着有一个空行
路径应该是连续的依次所走方块的位置
如果不存在这样的路径, 输出"impossible”

输入样例

输出样例：

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

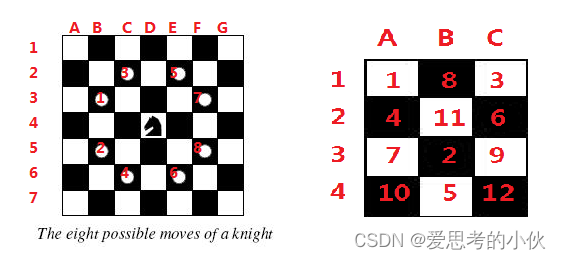
在这里插入图片描述

参考程序

#include<iostream>
#include<string>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=110;
int n,m,dis[][2]= {-1,-2, 1,-2, -2,-1, 2,-1, -2,1, 2,1, -1,2, 1,2};
int vis[N][N], s[N][2], flag=0;
void dfs(int x,int y,int step) {
   s[step][0]=x, s[step][1]=y, vis[x][y]=1;
   if(step==n*m) {
      flag=1; return;
   }
   for(int i=0; i<8; i++) {
      int tx = x+dis[i][0];
      int ty = y+dis[i][1];
      if(flag||vis[tx][ty]||tx<1||tx>n||ty<1||ty>m) continue;
      vis[tx][ty]=1;
      dfs(tx, ty, step+1);
      vis[tx][ty]=0;
   }
}
int main() {
//   freopen("data.in", "r", stdin);
   int t; scanf("%d", &t);
   for(int i=1; i<=t; i++) {
      scanf("%d%d",&n,&m);
      memset(vis, 0, sizeof(vis));
      flag=0;
      dfs(1,1,1);
      printf("Scenario #%d:\n",i);
      if(flag) {
         for(int i=1; i<=n*m; i++) {
            printf("%c%d",s[i][1]-1+'A',s[i][0]);
         }
      } else printf("impossible");
      printf("%s", i==t ? "\n":"\n\n");
   }
   return 0;
}

Avoid The Lakes POJ - 3620

问题描述
农夫约翰的农场在最近的一场风暴中被洪水淹没，而他的奶牛极度怕水的消息更是加剧了这一事实。
然而，他的保险公司只会根据他农场上最大的“湖”的大小来偿还他。

农场表示为一个包含 N 行和 M 列的矩形栅格。网格中的每个单元格要么是干燥的，要么是浸没的，其中K个单元格被浸没。正如人们所料，湖泊有一个中央细胞，其他细胞通过共享一条长边（而不是一个角）与之相连。任何与中央单元共享长边或与任何连接单元共享长边的单元都将成为连接单元，并且是湖泊的一部分。

输入格式
第1行：三个空格分隔的整数：N、M和K（1≤ N，M≤ 100，1≤ K≤ N×M）
第2…K+1行：第i+1行用两个空格分隔的整数描述了一个浸没位置，这两个整数是其行和列：R和C

输出格式
第1行：最大湖泊包含的单元数。

输入样例

输出样例：4

参考程序

#include<iostream> 
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e4+10;
int n,m,k,a,b,dis[][2]= {-1,0, 0,-1, 1,0, 0,1};
int ans=0,cnt=0,s[N][N];

void dfs(int x,int y){
    s[x][y]=0, cnt++;
    for(int i=0; i<4; i++){
        int tx=x+dis[i][0];
        int ty=y+dis[i][1];
        if(!s[tx][ty]||tx<1||tx>n||ty<1||ty>m) continue;
        dfs(tx,ty);
    }
}
int main(){
//    freopen("data.in", "r", stdin);
    scanf("%d%d%d", &n,&m,&k);
    for(int i=1; i<=k; i++) {
        scanf("%d%d",&a,&b); s[a][b]=1; 
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            if(s[i][j]==1){
                cnt=0;  dfs(i,j);
                ans=max(ans,cnt);
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

Dungeon Master POJ - 2251

问题描述

你进入了一个3D的宝藏地宫中探寻宝藏到了宝藏，
你可以找到走出地宫的路带出宝藏，或者使用炉石空手回家。
地宫由立方体单位构成，立方体中不定会充满岩石。
向上下前后左右移动一个单位需要一分钟。
你不能对角线移动并且地宫四周坚石环绕。
请问你是否可以走出地宫带出宝藏？如果存在，则需要多少时间？

输入格式

每个地宫描述的第一行为L，R和C（皆不超过30）。
L表示地宫的层数，R和C分别表示每层地宫的行与列的大小。
随后L层地宫，每层R行，每行C个字符。每个字符表示地宫的一个单元。
‘#‘表示岩石单元，’.‘表示空白单元。你的起始位置在’S’，出口为’E’。
每层地宫后都有一个空行。L，R和C均为0时输入结束。

输出格式

每个地宫对应一行输出。
如果可以带出宝藏，则输出 Escaped in x minute(s). x为最短脱离时间。
如果无法带出，则输出 Trapped!

输入样例

3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

参考程序

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int N=110;
int dis[][3]= {0,0,1, 0,0,-1, 0,1,0, 0,-1,0, 1,0,0, -1,0,0};
int l,r,c,sx,sy,sz,ex,ey,ez;
char s[N][N][N]; 
struct T {
    int x,y,z,step;
    T() {}
    T(int a,int b,int c,int d) {
        z=a, x=b, y=c, step=d;
    }
};
int bfs() {
    queue<T> que; que.push(T(sz,sx,sy,0));
    s[sz][sx][sy]='#';
    while(!que.empty()) {
        T temp = que.front(); que.pop();
        for(int i=0; i<6; i++) {
            int tx = temp.x+dis[i][0];
            int ty = temp.y+dis[i][1];
            int tz = temp.z+dis[i][2];
            if(tz<0||tz>=l||tx<0||tx>=r||ty<0||ty>=c) continue;
            if(s[tz][tx][ty]=='E') return temp.step+1;
            if(s[tz][tx][ty]!='#') que.push(T(tz,tx,ty,temp.step+1));
            s[tz][tx][ty]='#';
        }
    }
    return -1;
}
int main() {
//    freopen("data.in", "r", stdin);
    while(~scanf("%d%d%d\n",&l,&r,&c)) {
        if(l==0&&r==0&&c==0) break;
        for(int i=0; i<l; i++) {
            for(int j=0; j<r; j++) scanf("%s\n",s[i][j]);
            for(int j=0; j<r; j++) {
                for(int k=0; k<c; k++) {
                    if(s[i][j][k]=='S') {
                        sz=i, sx=j, sy=k; break;
                    }
                }
            }
        }
        int ans=bfs();
        if(ans!=-1) printf("Escaped in %d minute(s).\n", ans);
        else printf("Trapped!\n");
    }
    return 0;
}

Tram POJ - 1847

问题描述

萨格勒布有轨电车网络由许多十字路口和连接其中一些十字路口的轨道组成。每个十字路口都有一个道岔，指向驶出十字路口的一条轨道。当有轨电车进入十字路口时，它只能沿着道岔所指的方向离开。如果驾驶员想换一条路，他/她必须手动更换开关。当驾驶员从a交叉口开车到B交叉口时，他/她会尝试选择一条路线，以尽量减少他/她手动更换道岔的次数。
编写一个程序，计算从交叉口a行驶到交叉口B所需的最小转辙次数。

输入格式
输入的第一行包含整数N、A和B，由一个空白字符分隔，N是网络中的交点数，交点从1到N进行编号。
2<=N<=100，1<=A，B<=N
以下N行中的每一行都包含一个由单个空白字符分隔的整数序列。
第i条线中的第一个数字Ki（0<=Ki<=N-1）表示出第i个交叉点的钢轨数量。
接下来的Ki数字表示直接连接到第i个交点的交点。
第一个交叉口中的道岔最初指向列出的第一个交叉口的方向。

输出格式
输出的第一行也是唯一一行应该包含目标最小数。如果没有从A到B的路由，则该行应包含整数“-1”。

输入样例

输出样例：0
样例解释：
3 2 1 //有3个开关点，计算从第一个点a到第二个点b最少需要旋转几次
2 2 3 //第1个开关可以通向共2个点，2和3 ，通向2不需要旋转，通向3需要旋转1次
2 3 1 //第2个开关可以通向共2个点，3和1，通向3不需要旋转，通向1需要旋转1次

分析：读题有点麻烦，就是求一个最短路，数据小，floyed 即可。
参考程序

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=110, INF=0x3f3f3f3f;
int G[N][N];// G[i][j]从 i到 j的最短路径
void init(int n) {
    memset(G, 0x3f, sizeof(G));
    for(int i=1; i<=n; i++) G[i][i]=0; //自环
}
void floyed(int n) { // 弗洛伊德算法
    for(int k=1; k<=n; k++) { // 中间点，从 i到 j，中间只经过前 k个点
        for(int i=1; i<=n; i++) {   // 起点
            for(int j=1; j<=n; j++) { // 终点
                G[i][j]=min(G[i][j], G[i][k]+G[k][j]);
            }
        }
    }
}
int main() {
//    freopen("data.in", "r", stdin);
    int n,a,b,num,v;
    while(~scanf("%d%d%d",&n,&a,&b)) {
        init(n);
        for(int i=1; i<=n; i++) {
            scanf("%d", &num);
            for(int j=1; j<=num; j++) {
                scanf("%d", &v);
                if(j==1) G[i][v]=0;
                else G[i][v]=1;
            }
        }
        floyed(n);
        printf("%d\n", G[a][b]==INF ? -1 : G[a][b]);
    }
    return 0;
}

Til the Cows Come Home POJ - 2387

问题描述
阿狗经常找不到路，他和朋友在凌晨一点吃完海底捞后不知道怎么回学校。
市里有N个(2 <= N <= 1000)个公交站，编号分别为1…N。
公交站1是阿狗的位置,学校所在的位置是N。
所有公交站间共有T (1 <= T <= 2000)条双向路径。
阿狗为了锻炼未来的ACMer，决定让你帮他计算他到公司的最短距离。
保证这样的路存在。

输入格式
第一行：两个整数 T 和 N；
接下来T行：每一行都用三个空格分隔的整数描述一条路径。
前两个整数表示一条公交线路的起始点，第三个整数是路径的长度，范围为1到100。

输出格式
一个整数，表示回到学校的最小距离（不考虑步行）。

输入样例

输出样例：90

参考程序

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
typedef long long ll;
const int N=1e6+10, INF=0x3f3f3f3f;
int head[N],cnt=0,dis[N],vis[N],n,m;
struct T {
    int to,w,next;
    T() {}
    T(int a,int b):to(a),w(b) {}
    bool operator< (const T& t) const {
        return w > t.w;
    }
} G[N];
void add(int u,int v,int w) {
    G[++cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void dijkstra(int s) { // 迪杰斯特拉-朴素算法
    fill(dis, dis+N, INF);
    fill(vis, vis+N, 0);
    dis[s] = 0;
    for(int i=1; i<=n; i++) {
        int u=0, minv=INF;// u 当前集合最小值
        for(int j=1; j<=n; j++) {
            if(!vis[j] && dis[j]<minv) u=j, minv=dis[j];
        }
        if(u==0) break;
        vis[u]=1;
        for(int j=head[u]; ~j; j=G[j].next) {
            int v=G[j].to, w=G[j].w;
            if(dis[v] > dis[u]+w) dis[v] = dis[u]+w;
        }
    }
}
void pri_dijkstra(int s) {// 迪杰斯特拉-堆优化
    fill(dis, dis+N, INF);
    fill(vis, vis+N, 0);
    dis[s] = 0;
    priority_queue<T> que; que.push(T(s,dis[s]));
    while(!que.empty()) {
        T p=que.top();  que.pop();
        int u=p.to;
        vis[u]=1;
        for(int i=head[u]; ~i; i=G[i].next) {
            int v=G[i].to, w=G[i].w;
            if(dis[v] > dis[u]+w) {
                dis[v] = dis[u]+w;
                if(!vis[v]) que.push(T(v,dis[v]));
            }
        }
    }
}
int main() {
//    freopen("data.in", "r", stdin);
    fill(head, head+N, -1);
    scanf("%d%d", &m,&n);
    for(int i=1; i<=m; i++) {
        int u,v,w; scanf("%d%d%d", &u,&v,&w);
        add(u,v,w), add(v,u,w);
    }
//    dijkstra(1);
    pri_dijkstra(1);
    printf("%d\n", dis[n]==INF? -1 : dis[n]);
    return 0;
}

昂贵的聘礼 POJ - 1062

问题描述
你想娶酋长的女儿，但酋长要求你给一定数额金钱的聘礼。除了金钱外，酋长也允许你用部落里其他人的某物品加上一点钱作为聘礼。而其他人的物品也可以通过指定的另外一些人的某物品加上一些金钱获得。部落里的每个人有一个等级。你的整个交易过程涉及的人的等级只能在一个限定的差值内。问你最少需要多少金钱才能娶到酋长女儿。假定每个人只有一个物品。

输入格式
输入第一行是两个整数M，N（1 <= N <= 100），依次表示地位等级差距限制和物品的总数。
接下来按照编号从小到大依次给出了N个物品的描述。
每个物品的描述开头是三个非负整数P、L、X（X < N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和"优惠价格"。

输出格式
输出最少需要的金币数。

输入样例

输出样例：5250

分析：建图如下，求最短路，但是题目说需要考虑等级问题，那么就枚举等级 [l-m, l+m]，求最小值答案。
参考程序

#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
using namespace std;
const int N=110, INF=0x3f3f3f3f;
int n,m,head[N],dis[N],vis[N],cnt=0,a[N];
struct T{
    int to,w,next;
    T(){}
    T(int a,int b):to(a), w(b){}
    bool operator< (const T& t) const {
        return w > t.w;
    }
}G[N*N];  // 这里需要多开边集数组
void add(int u,int v,int w){
    G[++cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void pr(){
    for(int i=0; i<=n; i++){
        printf("%d : ", i);
        for(int j=head[i]; ~j; j=G[j].next){
            printf("(%d,%d) ", G[j].to, G[j].w);
        } puts("");
    }
}
void pri_dijkstra(int s,int l,int r){
    fill(dis, dis+N, INF);
    fill(vis, vis+N, 0);
    for(int i=1; i<=n; i++) if(a[i]<l ||a[i]>r) vis[i]=1;
    dis[s] = 0;
    priority_queue<T> que; que.push(T(s, dis[s]));
    while(!que.empty()){
        T temp = que.top();  que.pop();
        int u=temp.to;
        vis[u]=1;
        for(int i=head[u]; ~i; i=G[i].next){
            int v=G[i].to, w=G[i].w;
            if(dis[v] > dis[u]+w){
                dis[v] = dis[u]+w;
                if(!vis[v]) que.push(T(v, dis[v]));
            }
        }
    }
}
int main(){
//    freopen("data.in", "r", stdin);
    fill(head, head+N, -1);
    scanf("%d%d",&m,&n);
    for(int i=1; i<=n; i++){
        int p,l,x,t,v; scanf("%d%d%d",&p,&l,&x);
        a[i]=l;
        add(0, i, p);
        for(int j=1; j<=x; j++){
            scanf("%d%d",&t,&v);
            add(t, i, v);
        }
    }
//    pr(); 
    int ans=INF;
    for(int i=a[1]-m; i<=a[1]; i++){
        pri_dijkstra(0,i,i+m);
        ans = min(ans, dis[1]);
    }
    printf("%d\n", ans);
    return 0;
}

Agri-Net POJ - 1258

问题描述
农夫约翰被选为镇长！他的竞选承诺之一是将互联网连接到该地区的所有农场。他当然需要你的帮助。
农民约翰为他的农场订购了高速连接，并将与其他农民分享他的连接。
为了将成本降到最低，他想铺设最少数量的光纤，将他的农场连接到所有其他农场。
给出连接每对农场所需的光纤数量列表，您必须找到将它们连接在一起所需的最小光纤数量。
每个服务器场必须连接到其他服务器场，以便数据包可以从任何一个服务器场流向任何其他服务器场。
任何两个农场之间的距离都不会超过100000。

输入格式
输入包括几个案例。对于每种情况，第一行包含农场数量N（3<=N<=100）。
以下几行包含N x N连接性矩阵，其中每个元素表示农场到另一个农场的距离。
从逻辑上讲，它们是N行N个空间分隔的整数。
从物理上讲，它们的长度限制在80个字符以内，因此有些行会延续到其他行。
当然，对角线将为0，因为从农场i到农场本身的距离对于这个问题来说并不有趣。

输出格式
对于每种情况，输出一个整数长度，即连接整个农场所需的最小光纤长度之和。

输入样例

输出样例：28

参考程序
prim

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1e3+10;
int G[N][N],n,m,closest[N],lowcost[N],vis[N];

int prim(int u) {
    memset(vis, 0x00, sizeof(vis));
    vis[u] = 1;
    lowcost[u] = 0;
    for(int i=1; i<=n; i++) {
        closest[i] = u, lowcost[i] = G[u][i];
    }
    for(int i=1; i<n; i++) { // 将剩余 n-1个点加入集合
        int temp=INF, k=u;   // k 为在非生成树中寻找的最小节点
        for(int j=1; j<=n; j++) {
            if(!vis[j] && lowcost[j]<temp) {
                temp = lowcost[j], k=j;
            }
        }
        if(k==u) return -1; // 非联通图，不存在最小生成树
        vis[k] = 1;         // 标记加入生成树
        for(int j=1; j<=n; j++) {
            if(!vis[j] && G[k][j]<lowcost[j]) {
                closest[j] = k, lowcost[j] = G[k][j];
            }
        }
    }
    int ans=0;
    for(int i=1; i<=n; i++) ans += lowcost[i];
    return ans;
}
int main() {
//    freopen("data.in", "r",stdin);
    while(~scanf("%d",&n)) {
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) scanf("%d", &G[i][j]);
        }
        printf("%d\n", prim(1));
    }
    return 0;
}

kruskal

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1e6+10;
struct T{
    int u,v,w;
    T(){}
    T(int a,int b,int c):u(a),v(b),w(c){}
    bool operator< (const T& t) const{
        return w < t.w;
    }
}G[N];
int f[N],n,m;

int find(int x){
    if(x==f[x]) return x;
    return f[x] = find(f[x]);
}
int kruskal(int u){
    for(int i=1; i<=n; i++) f[i]=i;//初始化 
    sort(G+1, G+1+m);
    int ans=0, cnt=0;
    for(int i=1; i<=m; i++){
        int fu = find(G[i].u), fv = find(G[i].v);
        if(fu!=fv){
            f[fu] = fv;
            ans += G[i].w;
            cnt++; 
        }
        if(cnt==n-1) return ans;
    }
    return -1;
}
int main() {
//    freopen("data.in", "r",stdin);
    while(~scanf("%d",&n)) {
        m = 0; // 多组数据 
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) {
                int w; scanf("%d", &w);
                G[++m] = T(i,j,w);
            } 
        }
        printf("%d\n", kruskal(1));
    }
    return 0;
}

Network of Schools POJ - 1236

问题描述
许多学校都与计算机网络相连。
这些学校之间已经达成协议：每所学校都有一份向其分发软件的学校名单（“接收学校”）。
请注意，如果B在学校A的分布列表中，则A不一定出现在学校B的列表中。
您需要编写一个程序，计算必须接收新软件副本的学校的最小数量，以便软件根据协议到达网络中的所有学校（子任务a）。作为进一步的任务，我们希望通过将新软件的副本发送到任意学校，确保该软件将到达网络中的所有学校。为了实现这一目标，我们可能必须通过新成员扩展接收者名单。计算必须进行的最小扩展数，以便我们将新软件发送到任何学校，它将到达所有其他学校（子任务B）。一次延期意味着在一所学校的接收名单中引入一名新成员。

输入格式
第一行包含整数N：网络中的学校数量（2<=N<=100），学校由前N个正整数标识。
接下来的N行中的每一行都描述了接收机列表。
行i+1包含学校i的接收者的标识符。每个列表以0结尾。空列表的行中仅包含一个0。

输出格式
您的程序应该向标准输出写入两行。
第一行应包含一个正整数：子任务A的解。第二行应包含子任务B的解。

输入样例