MIT_单变量微积分_16

最新推荐文章于 2019-06-08 12:32:29 发布

原创最新推荐文章于 2019-06-08 12:32:29 发布 · 262 阅读

0 ·

CC 4.0 BY-SA版权

——单变量微积分专栏收录该内容

32 篇文章

订阅专栏

本文探讨了定积分的基本概念及其应用，通过将区域分割成无数小矩形来估算曲线下方的面积。同时，引入了黎曼和的概念，解释了如何通过极限过程将黎曼和转换为定积分，这是理解微积分中积分部分的关键。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.定积分

Ex:计算区域的面积。
在这里插入图片描述
(1)使用举行将其分成许多小块矩形。

Ex1: $f(x)=x^2(a=0) 如图所示：$

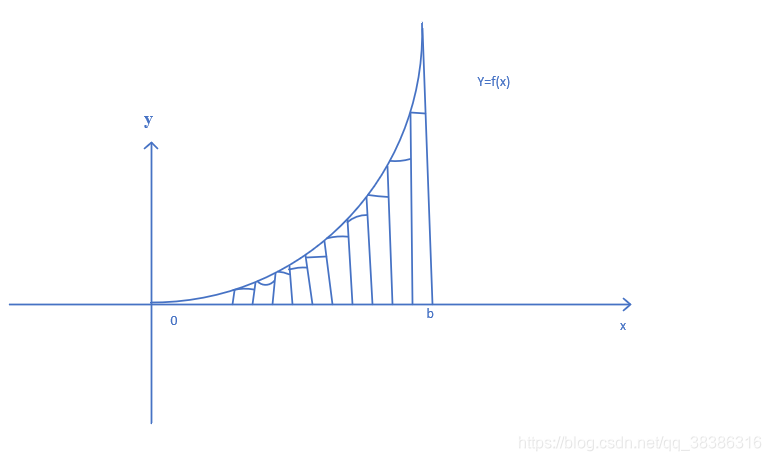
将其分成 $n$ 份矩形，每个矩形的长度为 $bn\frac{b}{n}$ ,得出：

$x$	$f (x)$
$bn\frac{b}{n}$	$b/n)^2$
$2bn\frac{2b}{n}$	$2b/n)^2$
$3bn\frac{3b}{n}$	$3b/n)^2$
…	…

$S=bn(bn)2+bn(2bn)2+bn(3bn)2+bn(4bn)2+...+bn(nbn)2=(bn)3(1+22+32+42+....+n2)=???S=\frac{b}{n}(\frac{b}{n})^2+\frac{b}{n}(\frac{2b}{n})^2+\frac{b}{n}(\frac{3b}{n})^2+\frac{b}{n}(\frac{4b}{n})^2+...+\frac{b}{n}(\frac{nb}{n})^2\\ =(\frac{b}{n})^3(1+2^2+3^2+4^2+....+n^2)\\ =???$
$13n3≤(1+22+32+42+....+n2)≤13(n+1)2(n+1)\frac{1}{3}n^3 \leq (1+2^2+3^2+4^2+....+n^2) \leq \frac{1}{3}(n+1)^2(n+1)$
这个式子也就是所谓的夹逼准则，至于几何推论可以想象以下那个金字塔的例子。
$13≤(1+22+32+42+....+n2)n3≤13(n+1)3n3=13(1+1n)3,n→∞时=13\frac{1}{3} \leq \frac{(1+2^2+3^2+4^2+....+n^2)}{n^3} \leq \frac{1}{3}\frac{(n+1)^3}{n^3}=\frac{1}{3}(1+\frac{1}{n})^3 ,n\rightarrow \infty 时=\frac{1}{3}$
Ex2:黎曼猜想：
把小矩形的长度变得很小很小。