MIT_单变量微积分_11

最新推荐文章于 2019-06-08 12:32:29 发布

原创最新推荐文章于 2019-06-08 12:32:29 发布 · 273 阅读

0 ·

CC 4.0 BY-SA版权

——单变量微积分专栏收录该内容

32 篇文章

订阅专栏

本文通过具体实例，详细解析了微积分中相关速率的问题，包括超速判断、圆锥形管子注水时水面上升速度的计算以及图形中某点最小值的求解过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 相关变率

Ex1:判断是否超速（ $95 f t / s$ ）,累到探测速度为 $80 f t / s$ , $dDdt=−80ft/s.\frac{dD}{dt}=-80ft/s.$

在这里插入图片描述
$x=D2−302,2xdxdt=2DdDdt,得出dxdt=−100ft/xx=\sqrt{D^2-30^2},2x\frac{dx}{dt}=2D\frac{dD}{dt},得出\frac{dx}{dt}=-100ft/x$

Ex2: 一个圆锥形的管子，顶部半径为 $4 f t$ ,高为 $10 f t$ ,注水速度为 $2 立方 / m i n$ ,当水深 $5 f t$ 时，水面上升的速度为多少？
在这里插入图片描述
解： $rh=410,dvdt=2\frac{r}{h}=\frac{4}{10},\frac{dv}{dt}=2$

$v=13πr2∗hv=\frac{1}{3}\pi r^2 *h$

$r=25hr=\frac{2}{5}h$

$v=13π(25h)2∗hv=\frac{1}{3}\pi(\frac{2}{5}h)^2*h$

$2=dvdt=π3(25)2∗3h2∗dhdt=425πh2dhdt2=\frac{dv}{dt}=\frac{\pi}{3}(\frac{2}{5})^2*3h^2*\frac{dh}{dt}=\frac{4}{25}\pi h^2\frac{dh}{dt}$

当 $h = 5$ 时， $dhdt=12πft/min\frac{dh}{dt}=\frac{1}{2\pi}ft/min$

Ex3:如果所示为固定两个顶点后画的图形，求 $y$ 得最小值，即 $y^{'} = 0$

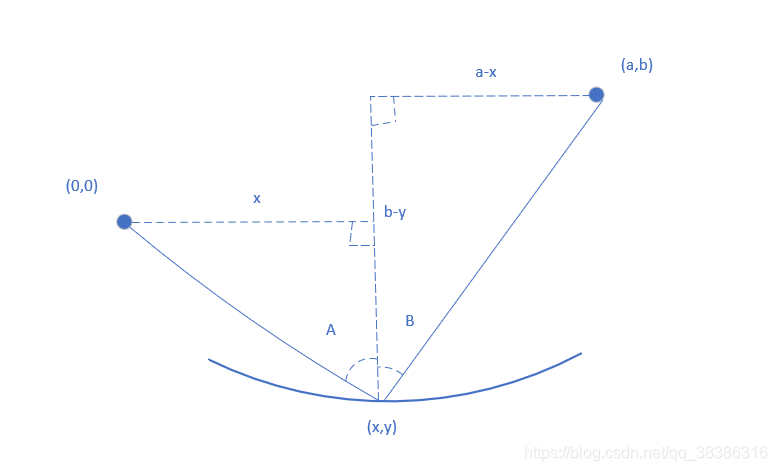
在这里插入图片描述
解： $x2+y2+(a−x)2+(b−y)2=L\sqrt{x^2+y^2}+\sqrt{(a-x)^2+(b-y)^2}=L$
使用隐函数微分法得：
$22∗x+yy′(x2+y2)12−(a−x)+(b−y)y′(a−x)2+(b−y)2=0xx2+y2=a−x(a−x)2+(b−y)2sinA=sinB\frac{2}{2}*\frac{x+yy'}{(x^2+y^2)^{\frac{1}{2}}}-\frac{(a-x)+(b-y)y'}{\sqrt{(a-x)^2+(b-y)^2}}=0\\ \frac{x}{\sqrt{x^2+y^2}}=\frac{a-x}{\sqrt{(a-x)^2+(b-y)^2}}\\ sin A= sinB$
即 $A = B$