稀疏传感器下的桥梁损伤识别

利用稀疏传感器网络自动识别土木基础设施中的密集损伤敏感特征

赛义德·库卡*，卢卡·兰迪，皮耶尔·保罗·迪奥塔尔维
意大利博洛尼亚大学DICAM系，博洛尼亚复兴大道2号，40136

摘要

由于监测系统的高成本，在区域层面广泛应用桥梁监测的情况仍然很少。然而，民用基础设施的老化以及日益增长的交通需求，迫切需要一种简单且自动化的工具来辅助应急管理。本文提出了一种集成算法，利用移动车辆识别动态和密集准静态结构特征。通过对通过车辆引发的原始加速度结构响应进行滤波，可实现模态参数和曲率影响线的识别。该过程的主要计算核心为卷积运算，因此能够高效实施。基于曲率定义的损伤指标，可在使用少量传感器的情况下，实现对结构异常的精确定位与量化。所提出的流程已在意大利A24高速公路的三座高架桥上进行了测试。此外，还建立了一个数值模型以评估该策略在损伤定位方面的潜力。

1. 引言

道路基础设施的失效会导致直接损失，包括维修或拆除/重建的成本，以及长期的间接影响，涉及紧急管理临时措施的成本、交通延误、绕行和事故，还可能导致应急车辆行程延长。对工业和当地商业造成的经济损失，以及随之而来的就业需求下降，构成了灾难性事件的整体框架，甚至可能造成最严重的人员伤亡损失。由于桥梁和高架桥老化以及交通需求的增长，结构退化正成为一个令人关切的严重问题。由于普遍缺乏资源，近年来的趋势是从传统的计划性维护转向基于状态的维护，即在某些指标显示出性能下降或即将失效时进行维护。这样，不经济的“坏了再修”方式将被更高效的“预防与预测”策略所取代。近几十年来，结构健康监测（SHM）系统已被证明是决策者优化维护工作或中断老旧基础设施正常使用的有力工具。尽管“信息从无害处”[1], ，但传统监测系统的高昂成本使基础设施所有者对投资持怀疑态度[2,3]。实际上，大多数民用基础设施需要大规模部署监测系统，以在区域范围内管理干预措施，从而涉及相当大的费用，而这些费用通常对于小型基础设施来说是不合理的。

由于无线传感器网络（WSNs）所用组件成本较低以及功耗优化系统的开发，[4],智能节点的密集分布正越来越多地应用于结构健康监测应用，但同时也带来了大量数据管理和同步方面的问题。为此，已提出多种针对无线传感器网络的结构识别算法，引入了用于数据管理和特征计算的去中心化策略。Quqa等人[5]最近提出了一种基于聚类滤波器组（CBFs）的去中心化算法，用于识别瞬时模态参数，可在星型拓扑网络中实现近实时应用。基于相同原理，模态置信分布（MAD）作为一种新型多变量信号的时频表示方法被提出，可用于解耦结构响应中混叠的模态贡献，并识别强时变结构的实时损伤敏感特征[6]。与广泛使用的经验模态分解（EMD）相比，该算法即使在处理非线性结构时也表现出更优的性能[7]。此外，在多种类型的输入激励下，该方法也获得了准确的识别结果。

尽管车辆交通是一种重要的激励源，相较于环境振动，其采集的记录具有较高的信噪比，但荷载的时间变异性可能不符合大多数运行模态分析（OMA）技术所依赖的稳态振动假设[8]。移动荷载通过时还可能改变结构的短时行为，使钢筋混凝土（RC）元素中的呼吸裂缝张开，并在车辆撞击伸缩缝时产生局部动力效应。OMA流程通常会舍弃包含此类效应的记录，而这些效应却可能表征结构的实际状态。此外，在移动荷载作用下采集的结构响应中蕴含的空间信息，可能揭示对结构健康监测（SHM）有价值的结构特征。Aloisio等人最近利用在移动荷载作用下采集的信号研究了钢筋混凝土高架桥，以识别其弹性模量[9]。Khan等人最近利用交通引起的振动以去中心化的方式识别桥基冲刷[10]。近年来，驾驶式监测（即使用安装在移动车辆上的传感器采集的数据）在学术界获得了越来越多的关注[11]。Yang等人开展了从通过车辆的响应中提取桥梁频率的开创性研究，从而提出了“驾驶式监测”[12],的概念。

Gonz´alez等人则采用相同方法成功识别了阻尼比[13] 。此外，Aloisio等人[14]利用经过的仪器化车辆的响应，识别了前述研究中相同高架桥的抗弯刚度[9]。此外，文献中还考虑使用其他测量设备，例如视频摄像机[15]和动态称重系统[16] ，以推断移动荷载的相关信息，并已开发出先进的结构健康监测策略，结合布置在结构和移动车辆上的传感器，以更准确地描述车辆‐桥梁相互作用[17]。

最近的研究致力于通过分析移动荷载引起的准静态效应来识别密集的结构特征（即描述大量位置处的结构行为）。He等人提出了一种损伤识别方法，该方法能够利用低速移动传感器采集的位移数据量化损伤，从而仅收集试件的准静态响应[18]。Cavedas等人使用位移和转角测量数据评估了移动主成分分析（MPCA）和鲁棒回归分析（RRA）在该目的下的性能[19]。其他技术则尝试通过分析布置在桥梁上的传感器而非移动车辆上采集的记录来获得类似结果，这些传感器通常对车‐桥相互作用效应较不敏感。Frøseth等人提出了一种高效的频域解卷积方法来计算结构的位移影响线[20]。然而，在该技术中，荷载必须预先已知。在时域中，Zheng等人提出了一种基于正则化最小二乘法的有效方法，利用多轴车辆激励进行影响线识别[21]。文献[22]综述了采用频域和时域模型的最新方法，并进行了深入比较。Hester等人利用梁端部测得的转角数据实现了损伤的准确识别与定位[23]。除了转角和位移外，应变测量也得到了广泛应用[24–26]。然而，加速度计作为目前结构健康监测中最广泛使用的传感器，由于记录低频成分存在困难，极少被用于准静态结构特征的识别。尽管如此，近年来的MEMS技术以及更传统的力平衡加速度计（FBA）能够采集低至直流的低频振动，因此可用于此目的。

本文的目的有三个：

1) 验证MAD在[6]中已提出的用于长期应用的可行性，将其应用于承受移动荷载的民用基础设施。尽管基于MAD的识别算法相较于其他文献中的方法已证明具有多种优势（例如，瞬时模态的自动识别和提取）即使在存在窄带干扰[6]和非线性效应[7]的情况下，在多种场景中，移动荷载和短信号窗口也带来了进一步的挑战，需要加以解决，以提出适用于运营中的民用基础设施的有效结构健康监测策略。

2) 提出一种统一自动识别策略，利用稀疏传感器网络（可少至仅一个传感装置）收集的加速度数据，来估计密集的准静态结构特征和模态参数。该过程仅基于加速度记录，无需额外设备追踪车辆位置。此外，所提出的用于车辆通过相关信号窗口的自动选择与处理的算法，使该方法特别适用于众包云计算应用。

3) 测试已识别的准静态结构特征在损伤定位与量化方面的潜力。由于本文研究的准静态特征具有明确的物理意义，提出了一种基于曲率的损伤敏感特征（DSF），避免了传统方法从已识别振型中计算曲率时通常所需的复杂过程（以及相应的近似处理）。该新方法带来了显著优势：能够在有限（因而低成本）的监测设备条件下准确识别结构异常，适用于大范围监测，并且无需数据同步。此外，与大多数文献方法不同[27,28], ，该方法在量化损伤程度时无需了解结构质量信息，也无需使用有限元模型。

前两点得到了在意大利A24高速公路三座高架桥上采集的加速度数据的分析结果的支持，这些结果已在Aloisio等人[9,14,29,30]的多项研究中进行了分析。此外，还报告了数值案例研究在不同损伤情景下的结果，以展示提出的方法在损伤检测、定位和量化方面的潜力。

2. 移动荷载作用下的结构识别

静定体系（如简支梁）通常被用于钢筋混凝土桥梁和高架桥的设计，因为它们能够适应环境荷载（如温度）引起的膨胀（或收缩）效应，而这些效应在超静定结构中会产生非期望应力状态。在本研究中，简支梁将被视为常见钢筋混凝土高架桥某一跨的代表。

结构健康监测领域的文献报道了多个动态识别方法的有效性受到结构非线性影响的案例[31]。此外，在土木结构中，损伤通常与非线性程度的增加相关[32]。然而，材料和几何非线性以及与边界条件相关的非线性通常由显著位移激活。由于本文提出的方法是针对常规交通荷载设计的，因此假设结构处于小位移状态，从而表现为线性行为。

一般来说，等截面线性简支梁在作用于结构轴线正交方向的通用荷载函数p(z,t)下的运动方程可以表示为

$$
\mu \frac{\partial^2 u(z, t)}{\partial t^2} + d \frac{\partial u(z, t)}{\partial t} + EI \frac{\partial^4 u(z, t)}{\partial z^4} = p(z, t) \quad (1)
$$

其中μ为单位长度质量，d为阻尼系数，EI为抗弯刚度，由材料的弹性模量E和截面惯性矩I给出。在公式（1）中，u（z，t）是空间（z）和时间（t）的函数，表示结构在荷载方向上的位移响应，而∂kf/∂xk算子表示第k阶函数f关于x的导数。利用叠加原理，结构响应可以表示为模态响应的线性组合

$$
u(z, t) = \sum_{m=1}^{\infty} \phi_m(z) q_m(t) \quad (2)
$$

其中ϕm(z)是结构的第m阶振型，qm(t)是时间的函数，其在频域中围绕阻尼后的第m阶圆频率ωd,m出现峰值，在低阻尼情况下，可将其视为结构的第m阶固有（圆）频率

$$
\omega_m = \frac{m^2 \pi^2}{l^2} \sqrt{\frac{EI}{\mu}} \quad (3)
$$

其中l为梁的长度。在自由振动条件（即p(z,t)= 0）下，若阻尼较小，则结构响应可近似为

$$
u(z, t) = \sum_{m=1}^{\infty} c_m \sin\left(\frac{m\pi z}{l}\right) e^{-\xi \omega_m t} \sin(\omega_m t) \quad (4)
$$

其中cm表示依赖于初始条件的常数，ξ表示模态阻尼比，此处假设所有振动模态的模态阻尼比相等。

通常，在结构健康监测应用中，使用加速度计来采集结构响应。在自由振动情况下，采集的加速度可以用以下方程描述：

$$
\frac{\partial^2 u(z, t)}{\partial t^2} = \sum_{m=1}^{\infty} c_m \sin\left(\frac{m\pi z}{l}\right) \ddot{q}_m(t) \quad (5)
$$

其中

$$
\ddot{q}_m(t) = \omega_m^2 e^{-\xi \omega_m t} \left[ (\xi^2 - 1)\sin(\omega_m t) - 2\xi \cos(\omega_m t) \right] \quad (6)
$$

因此可以计算加速度的傅里叶变换为

$$
A_a(z,f) = \mathcal{F}\left[\frac{\partial^2 u(z, t)}{\partial t^2}\right] = \sum_{m=1}^{\infty} c_m \sin\left(\frac{m\pi z}{l}\right) Q_m(f) \quad (7)
$$

其中Qm(f)表示与第m阶模态相关的单自由度系统（SDOF）的归一化传递函数：

$$
Q_m(f) = \frac{\omega_m^3 (1 + \xi^2) + 4j\pi \xi \omega_m^2 f}{\omega_m^2 + (\xi \omega_m + 2j\pi f)^2} \quad (8)
$$

现考虑一个幅值为P、以恒定速度v移动且具有可忽略质量的单个移动荷载，其荷载函数可表示为p(z,t)=Pδ(z − vt)，若阻尼较小，则结构的位移响应变为[33]：

$$
u(z, t) = \frac{Pl^3}{48EI} \sum_{m=1}^{\infty} \frac{1}{m^2 (m^2 - \alpha^2)} \sin\left(\frac{m\pi z}{l}\right) \left[ \lambda_m(t) - \frac{\alpha}{m} e^{-\xi \omega_m t} \sin(\omega_m t) \right] \quad (9)
$$

with

$$
\alpha = \frac{v l}{\pi} \sqrt{\frac{m}{EI}} \quad (10)
$$

$$
\lambda_m(t) = \sin\left(\frac{m\pi v t}{l}\right) \prod\left(t - \frac{1}{2}\right) \quad (11)
$$

其中∏(t)是一个矩形函数，用于将λm(t)的支撑限制在区间t ∈[0,l/v], 内，即荷载位于梁上时的情况，δ表示狄拉克δ函数。通过二阶导数得到的加速度响应因此为：

$$
\frac{\partial^2 u(z, t)}{\partial t^2} = -\frac{Pl^3}{48EI} \sum_{m=1}^{\infty} \frac{1}{m^2 (m^2 - \alpha^2)} \sin\left(\frac{m\pi z}{l}\right) \left{ \left(\frac{m\pi l v}{l}\right)^2 \lambda_m(t) + \frac{\alpha}{m} \ddot{q}_m(t) \right} \quad (12)
$$

及其傅里叶变换为

$$
A_v(z,f) = \mathcal{F}\left[\frac{\partial^2 u(z, t)}{\partial t^2}\right]
= -\frac{Pl^3}{48EI} \sum_{m=1}^{\infty} \frac{1}{m^2 (m^2 - \alpha^2)} \sin\left(\frac{m\pi z}{l}\right) \left[ L_m(f) - \frac{\alpha}{m} Q_m(f) \right] \quad (13)
$$

其中Lm(f)是一个依赖于移动荷载准静态效应的函数，其表达式如下：

$$
L_m(f) = \frac{\pi v m^3}{2l (l^2 f^2 / v^2 - m^2 / 4)} e^{j\pi (m/2 - l f / v)} \sin(\pi l f / v - m\pi / 2) \quad (14)
$$

比较式(7)和(13)可以看出，除了常数项外，第二个方程多出一个由式(14)表示的附加项。通过将调制定理应用于sinc函数，可得到Lm(f)的表达式，如附录A所示。该函数在频率值随m增大而增大的位置出现尖锐峰值，但其幅值相对较低。此外，Lm(f)随f²的增大而减小。因此可以认为，项Lm(f)仅在低频范围对结构响应有不可忽略的贡献。另一方面，函数Qm(f)包含了结构第m阶振动模态的信息，因此通常主导响应谱的中高频成分。

车辆交通虽然作为移动荷载的集合，但在结构振动响应中引发多种效应，即（1）由于通过车辆重量引起结构挠度而产生的准静态效应，（2）由于惯性力、弹性力和耗散力之间瞬时平衡而产生的动力效应，以及（3）短期效应，此处称为“噪声”，主要由车轮与不平整路面之间的相互作用引起。第一种现象如公式(14)所述，与瞬时车辆位置密切相关，并主要影响结构响应频谱中最低（通常为亚赫兹）频率范围。第二类效应可建模为一组结构振动模态的叠加，如公式(8)所述，对于最常见的钢筋混凝土高架桥，其首个模态通常占据几赫兹到几十赫兹的频率范围。最后，噪声影响整个频谱，其大部分能量集中在较高频率区域。

由于响应谱具有特定的结构，通过分别处理不同的频带，可以分析不同的结构特征。本文关注低频范围，旨在提取与车辆位置（即影响线）相关的准静态损伤敏感特征，以及首要主导动态贡献的模态参数（即固有频率和振型的稀疏估计）。

如参考文献[6],所示，MAD可用于构建自适应滤波器组，从而从不同布设传感器的位置采集的结构响应中提取解耦模态贡献。在上述研究中，使用小波滤波器组提取了临界采样信号分量，旨在降低识别参数的权重。此外，如果结构可被建模为线性时不变(LTI)系统，则可采用静态滤波器组，以提高识别过程的效率[5]。本文在以下假设条件下，将上述概念应用于民用基础设施的结构识别：

1) 将车辆建模为单个常数荷载，忽略车轮轴之间的间距；

2) 每次仅有一辆车辆以恒定速度通过桥梁；

3) 忽略车桥耦合效应。

前两个假设允许将荷载函数视为p(x,t) = Pδ(x − vt)。如果存在多个车轴，则应考虑响应谱中某些频率值的抑制。然而，在接下来的章节中将表明，第一个假设通常可以合理地成立。此外，由于钢筋混凝土基础设施中单跨的长度较短，在流畅交通情况下，第二个假设通常可以被接受。最后，关于第三点，相对于普通汽车而言，钢筋混凝土基础设施通常具有较大的质量。

在接下来的章节中，提出了两种识别方法，分别基于低频效应和（中）高频效应，以获取不同的结构特征，这些特征可能对评估结构完整性特别重要。

2.1. 低频效应

对车辆以恒定速度v通过时，在距离第一支座 ζl （其中 ζ< 1）的 D位置t ∈[0,l/v],处采集的结构加速度响应应用亚赫兹低通滤波器（12），可以定义

$$
h(\zeta)[t] = \left( \frac{\partial^2 u(z,t)}{\partial t^2} \bigg| {z=\zeta l} * b_0 \right)[t]
\cong -\frac{Pl^3}{48EI} \sum {m=1}^{\gamma} \frac{\pi^2 v^2 \sin(m\pi \zeta)}{l^2 (m^2 - \alpha^2)} \sin\left(\frac{m\pi v t}{l}\right) \quad (15)
$$

其中*是卷积算子，b₀[τ]是低通滤波器的脉冲响应，γ表示频率成分主要位于亚赫兹区间的少量贡献。假设车辆行驶距离为z= vt，可得到一个空间函数，该函数表示结构位移影响线关于空间的二阶导数：

$$
h(\zeta)[z] = \sum_{m=1}^{\gamma} h(\zeta) m[z] \cong \sum {m=1}^{\gamma} -\frac{Pl^3}{48EI} \frac{\pi^2 v^2 \sin(m\pi \zeta)}{l^2 (m^2 - \alpha^2)} \sin\left(\frac{m\pi z}{l}\right) \quad (16)
$$

h(ζ)[z] 因此是归一化位置ζ处梁的曲率影响线，因此也与影响线成正比弯矩图的直线。根据麦克斯韦‐贝蒂互等功定理，式(16)也可解释为在布设传感器的位置静态施加力P时梁的挠度形状的曲率。

需要注意的是h(ζ)[z]可通过在结构上布设单个传感装置进行识别，从而根据采集数据的采样频率，提供结构行为的密集描述。此外，曲率是一种公认的损伤敏感特征，通常通过对有限传感器识别出的振型进行二次求导获得。传统方法通常会引入计算误差（例如由于使用中心差分法），这可能在含噪声的识别参数存在的情况下影响结果的鲁棒性。此外，曲率通常仅能在布设传感器的位置进行估计。相反地，提出的方法利用采集的加速度推断潜在连续位置处的曲率信息，且在求导过程中无需进行任何近似。

考虑由双轴组成的荷载，通过计算h(ζ)[z]*εw[z],可得到一个等效的空间函数，其中εw[z]= δ[z]+ δ[z+w], w为车轮轴之间的距离，δ[z]为离散的狄拉克δ函数，从而得到

$$
h(\zeta)[z] * \varepsilon_w[z] = h(\zeta)[z] + h(\zeta)[z + w] \quad (17)
$$

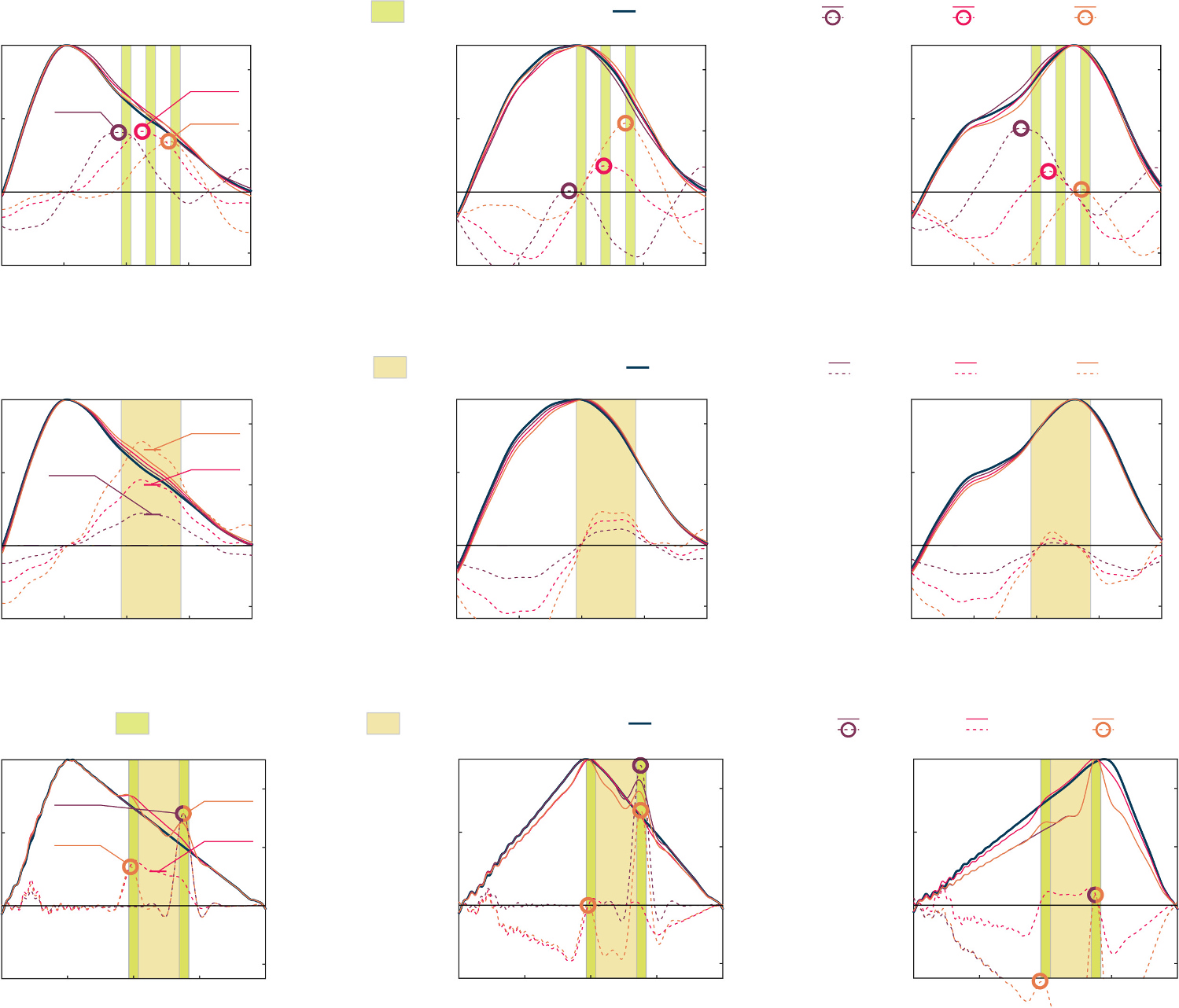
从物理意义上讲，该函数表示当第一个荷载位于位置z、第二个荷载位于位置z+w时，梁曲率的影响线。在频域中，公式(17)的谱可以通过简单的逐点乘积得到，即H(ζ)[f]Ew[f], ，其中H(ζ)[f]和Ew[f]分别为h(ζ)[z]和εw[z],的谱，如图1所示。考虑频率值f_s^(1)和fs，其定义为

$$
f_s^{(1)} = \left(s + \frac{1}{2}\right) \frac{v}{l} \quad (18)
$$

$$
f_s = \left(s - \frac{1}{2}\right) \frac{v}{w} \quad (19)
$$

表示s阶零点的H₁(ζ)[f] （即h₁[z]的频率谱）和Ew[f], ，可以假设当f₁^(1) ≪ f₁,时，即w ≪ l时，H(ζ)[f] ≅ H(ζ)[f]Ew[f]成立。特别地，假设极限

$$
\frac{f_1^{(1)}}{f_1} = \frac{3w}{l} \leq \frac{1}{3} \quad (20)
$$

将确保双荷载对H(ζ)的影响最多为13%。因此，从几何限制角度可设定为l ≥ 10w。该条件在大型民用基础设施情况下通常可以成立。然而，多荷载效应通常会产生更平滑的影响线。对于双轴的具体情况，这一点可以通过分析观察到，因为Ew[f]的作用是减小h(ζ)[z]中较高可感知贡献（具有接近γ的m指数）部分。由于高频贡献被衰减，最终得到的空间函数更平滑。

除了上述几何约束外，加速度计的采样频率应根据影响线所需的空间分辨率来选择。具体而言，考虑车辆速度v和所需的空间分辨率r，可得到最小采样频率为fs = v/r[34]。

2.2. 高频效应

单个移动荷载作用下结构响应谱的高频范围类似于自由振动状态下得到的响应谱，如公式(7)所示。此处，求和项中的每一项对应于结构的不同共振频率，并在频率域中围绕频率ωm附近呈现峰值。假设布置在结构上的第i个加速度计采集的信号由表示结构响应的部分和仪器噪声项ηi[t],组成，如图2所示，则公式(5)可重写为

$$
x_i[t] = \sum_{m=1}^{\infty} \phi_{i,m} \ddot{q}_m[t] + \eta_i[t] \quad (21)
$$

其中xi[t]是由第i个传感器采集的加速度，而ϕi,m是第i个振型中第m个模态的元素。假设噪声项为白高斯噪声，即具有理想的平坦谱，则式（21）求和项中的每个模态贡献在频率上具有有限范围，在该范围内结构响应高于仪器噪声。因此，可通过以系统固有频率为中心、带宽等于超过噪声阈值的频带的合适带通滤波器，利用其脉冲响应bm[τ]来提取模态响应。

最近研究表明，这些滤波器可以同时生成并应用于采集的数据，通过MAD自适应地提取模态贡献[6]。MAD是对多变量结构响应的二维表示，能够在频率和时间上突出不同模态贡献的存在。因此可用于自动识别和滤除模态响应。本文简要介绍了MAD的主要概念；感兴趣的读者可参考文献[6]以获得更详尽的理论背景。然后，基于该技术生成了一种适用于在移动荷载作用下民用基础设施中提取模态贡献的滤波器组。同时还展示了如何从解耦模态响应中识别模态参数，即固有频率和振型。

2.2.1. 模态置信分布

Applying a narrow bandpass filter bm[τ]截止频率ωm − ϵ和ωm+ ϵ到结构响应xi[t],其中ϵ是一个足够小的数，而ωm是结构的共振频率，滤波后的结构响应可表示为考虑公式(21)求和项中的单个项

$$
y_{i,m}[t] \cong \phi_{i,m} ( \ddot{q} m * b_m )[t] + \eta {i,m}[t] \quad (22)
$$

其中ηi,m[t]为滤波后的噪声分量。如图2(b)所示， ¨qm[t]的主要成分确实通常集中在较窄的频率范围内。忽略噪声分量，并对所有布设传感器的位置计算yi,m[t] ，可得到结构瞬时第i个元素的第m阶模态振型ϕm[t]的估计值

$$
\phi_{i,m}[t] \cong \frac{x_{i,m}[t]}{x_{r,m}[t]} \quad (23)
$$

其中r表示用于归一化的参考位置。还应注意，若ϵ足够小，则具有略微不同截止频率（例如ωm 和ωm + 2ϵ）的带通滤波器可提供相当准确的第m阶振型估计值。

另一方面，使用一个以频率bk[τ]为中心的滤波器，且该频率远离结构的共振频率，则ωk的贡献在式ηi,m[t]中很可能超过结构响应。此外，考虑另一个具有不同频率范围且远离ωm的滤波器bk+1[τ] ，由于白高斯噪声的特性，滤波后的分量与前一个分量不相关。

通常，使用通用带通滤波器(23)计算得到的式bk[τ]的结果可解释为结构在频率ωk处评估的瞬时工作变形模式（ODSs）的一个元素。本文中，将使用两个不同的符号来表示振型（即ϕ）和工作变形模式（ODSs）（即φ）。此外，下标m表示一个

和频域(b)中的模态分量；时域(c)和频域(d)中的带通滤波器)

结构的振动模态，而k表示一个通用频带。需要注意的是，只有当ωk足够接近系统的固有频率ωm时，工作变形模式φk才会成为第m阶振型ϕm的估计值。此外，若使用由截止频率连续的窄带通滤波器组成的滤波器组，则只有当第k个频带接近系统共振频率时，工作变形模式φk[t]才会在时间上持续相似于φk+1[t] 。此处，“持续”一词指的是时间上的持续性，因为两个连续工作变形模式之间可能由于瞬时相似的噪声成分而产生随机相似性。MAD旨在量化并定位时频平面上的此类相似性。具体而言，MAD矩阵M的元素定义为

$$
M_{k,t} = \frac{|\phi_k^T[t] \phi_{k+1}[t]|^2}{(\phi_k^T[t] \phi_k[t])(\phi_{k+1}^T[t] \phi_{k+1}[t])} \quad (24)
$$

介于0和1之间，接近1的值表示连续频带（即k和k+1）中存在相似的工作变形模式（ODSs），而接近0的值表示存在正交的连续工作变形模式（ODSs）。因此，时间‐频率（t‐k）平面中的高值区域表示接近系统固有频率的频带。其余部分平面则由贝塔分布噪声填充。

文献中用于生成MAD的带通滤波器是通过小波变换获得的。在[6],中，使用小波包滤波器组生成临界采样变换系数，以降低分布的权重。相反地，在[7],中，采用过完备小波展开来构建滤波器，以提取结构在强短时事件期间非线性正则模态的过采样表示。在这两种方法中，帕塞瓦尔’定理支持了将φk[t]视为系统的工作变形模式（ODSs）的假设。

2.2.2. 解耦模态贡献的提取

In this study, wavelet analysis filters of the Fej´er‐Korovkin族计算MAD，实现一种无下采样的平稳小波包变换(SWPT)。然而，也可使用任何线性时频分解（如傅里叶复指数或其他小波函数）的滤波器来实现此目的。

考虑与第k个分量相关联的等效SWPT分析滤波器的脉冲响应，可通过滤波采集的加速度xi[t]来计算结构的工作变形模式（ODSs）：

$$
\varphi_{i,k}[t] = (x_i * g_{a,k})[\tau] \quad (25)
$$

在公式(25)中，φi,k[t]是小波包变换（SWPT）第k= 1,…, 2ⁿ层的小波分量，该变换的层数为n。包含所有布设传感器的位置处计算得到的元素φi,k[t]的向量φk[t]表示结构在第k个频带的瞬时ODS，可用于公式(24)中计算MAD。

可以通过对MAD值设置阈值来选择包含结构相关信息的时频平面区域。具体而言，使用用户定义的阈值θ，仅考虑元素Mk,t ≥ θ以用于识别解耦模态贡献。在[6],中讨论了选择最优θ阈值的不同准则，表明其依赖于传感器数量。满足条件Mk,t ≥ θ的元素可以通过聚类算法划分为不同的集合。在[6],中，采用MAD和模态置信准则(MAC)的高值区域的图像分割来定义模态簇。相反地，在[7],中使用了k均值算法，并结合自组织映射来确定簇的数量。本研究采用基于密度的带噪声应用空间聚类 (DBSCAN)算法进行聚类，该算法不需要预先知道簇的数量[35]。

在聚类过程结束时，每个簇将对应结构的一个不同模态。考虑第m个簇，相关的“聚类”滤波器可用于提取第m个模态在第t个时刻，所有布设传感器的位置的贡献值可以计算为

$$
b_m^{(t)}[\tau] = \sum_{k=k_1}^{k_2} (g_{a,k} * g_{s,k})[\tau] \quad (26)
$$

其中，k= k1,…，k2 是第m个簇中所包含的工作变形模式（ODSs）的索引。模态分量xi,m[t] 可通过以下方式使用聚类滤波器提取：

$$
x_{i,m}[t] = (x_i * b_m^{(t)})[t] \quad (27)
$$

需要注意的是，bm(t)的截止频率会根据聚类过程的结果随时间变化。这使得滤波器组具有自适应性，并能够跟随由于环境与运行条件变化引起的结构行为变化。

2.2.3. 多个移动荷载的考虑

Although the application of the MAD-based分解算法与冲击荷载或宽带噪声激励情况类似，但多荷载的存在理论上会影响该过程的结果。特别是，考虑一辆具有两个车轮轴的车辆时，由于图1(d)中所示荷载函数的特定频谱，结构响应中接近fr的频率会被抑制。然而，在实际应用中，由于其他车辆通过相邻跨所传递的振动–以及其他荷载（如风）–将形成更复杂的荷载函数，其可表示为以下形式：

$$
p(z, t) = \upsilon(z, t) + P[\delta(x - vt) + \delta(x - w - vt)] \quad (28)
$$

其中υ(z,t)是由于环境与运行振动引起的附加分布噪声函数。将结构视为线性系统，其结构响应将包含移动荷载和环境现象的共同影响。尽管前者的影响可能占主导地位，但其他效应仍会产生结构响应的贡献，这些贡献分布在接近fr的频谱范围内。MAD中产生高值区域的工作变形模式（ODSs）之间的相似性是在向量意义下定义的（余弦相似度），即各元素间比值相似的ODSs将生成接近1的MAD值，而与φk[t]各个具体元素的幅值无关。因此，MAD不直接依赖于信号分量的幅值。正因如此，如果项υ(z,t)产生的结构响应在整个频率谱内均超过加速度计的噪声底电平，则MAD对多荷载导致的被抑制频带具有鲁棒性。

3. 民用基础设施结构健康监测的新策略

在第2.1节中，展示了一种利用单个传感器估计被建模为简支梁的结构密集型准静态特征的方法。具体而言，采用低通滤波器从加速度数据中提取结构的曲率影响线。此外，在第2.2节中，将MAD的理论框架扩展到移动荷载的情况。结果表明，可以使用自适应带通滤波器提取解耦的模态响应。第一类特征可提供有关结构异常位置的有价值信息，并能大致反映损伤程度。然而，这些特征对噪声和动力效应较为敏感。另一方面，模态参数仅在布设传感器的位置定义，但通常对噪声更具鲁棒性。因此，结合上述两类特征所获得的信息，可能有助于判断结构损伤的存在、大致位置及其损伤程度。接下来，基于这些概念提出了一种针对民用基础设施的新型结构健康监测策略。具体而言，首先介绍一种包含能够提取准静态和动态特征的滤波器的滤波器组。然后，提出一种基于已识别的特征的损伤识别方法。

3.1. 结构识别

考虑一组列向量bj(t) ，其中包含脉冲响应b(t)j[τ]的系数，其中τ= 1,…,N
N为滤波器长度，在第t个时间点的滤波器组矩阵可表示如下：

$$
\mathbf{B}_t = [\mathbf{b}_0, \mathbf{b}_1^{(t)}, …, \mathbf{b}_p^{(t)}] \quad (29)
$$

这里，术语$\mathbf{b}_0$包含第2.1节中用于提取准静态结构特征的低通滤波器$b_0[\tau]$的系数。在本研究中，假设$b_0$不依赖于时间点，即低通滤波器不随时间变化，因此省略了上标$(t)$。另一方面，$\mathbf{b}_j^{(t)}$中的项，其中$j= 1,…,p$表示自适应的时间相关带通滤波器。

考虑一个形式为$\mathbf{X}_t$的矩阵

$$
\mathbf{X} t = [\mathbf{x} {t,1}, \mathbf{x} {t,2}, …, \mathbf{x} {t,r}] \quad (30)
$$

其中$\mathbf{x}_{t,i}$是列向量，包含加速度信号$x_i[t]$在区间$[t - N/2, t+N/2]$内的样本，可计算得到一组分解信号：

$$
\mathbf{Y} t = \mathbf{X}_t^T \mathbf{B} =
\begin{bmatrix}
y {1,0}[t] & y_{1,1}[t] & \cdots & y_{1,p}[t] \
y_{2,0}[t] & y_{2,1}[t] & \cdots & y_{2,p}[t] \
\vdots & \vdots & \ddots & \vdots \
y_{r,0}[t] & y_{r,1}[t] & \cdots & y_{r,p}[t]
\end{bmatrix} \quad (31)
$$

需要注意的是，当改变$z= vt$中的变量时，元素$y_{i,0}[t]$表示荷载施加在$z$时第$i$个位置处的曲率估计值。相反地，根据麦克斯韦‐贝蒂互等功定理，$y_{i,0}[t]$也可解释为在第$i$个布设传感器的位置施加静载荷时，在$z$处产生的结构曲率。另一方面，$y_{i,m}[t]$且$m= 1,…,p$的项表示在第$i$个位置采集的第$m$阶模态响应的第$t$个样本。

当移动荷载进入和离开监测桥梁跨径时，由于荷载通过桥梁接缝时的动力效应，通常会记录到加速度峰值。这些峰值可在自动化程序中用于触发准静态和动力结构特征的计算。在这些时间中已识别的参数因此，可以通过考虑不同的通过车辆来对区间进行平均，以提高估计的鲁棒性。特别是，位置$\zeta l$（即第$i$个布设传感器的位置）处的曲率影响线可以计算为

$$
h^{(\zeta)}[z] \big| {z=vt} = y {i,0}[t] \quad (32)
$$

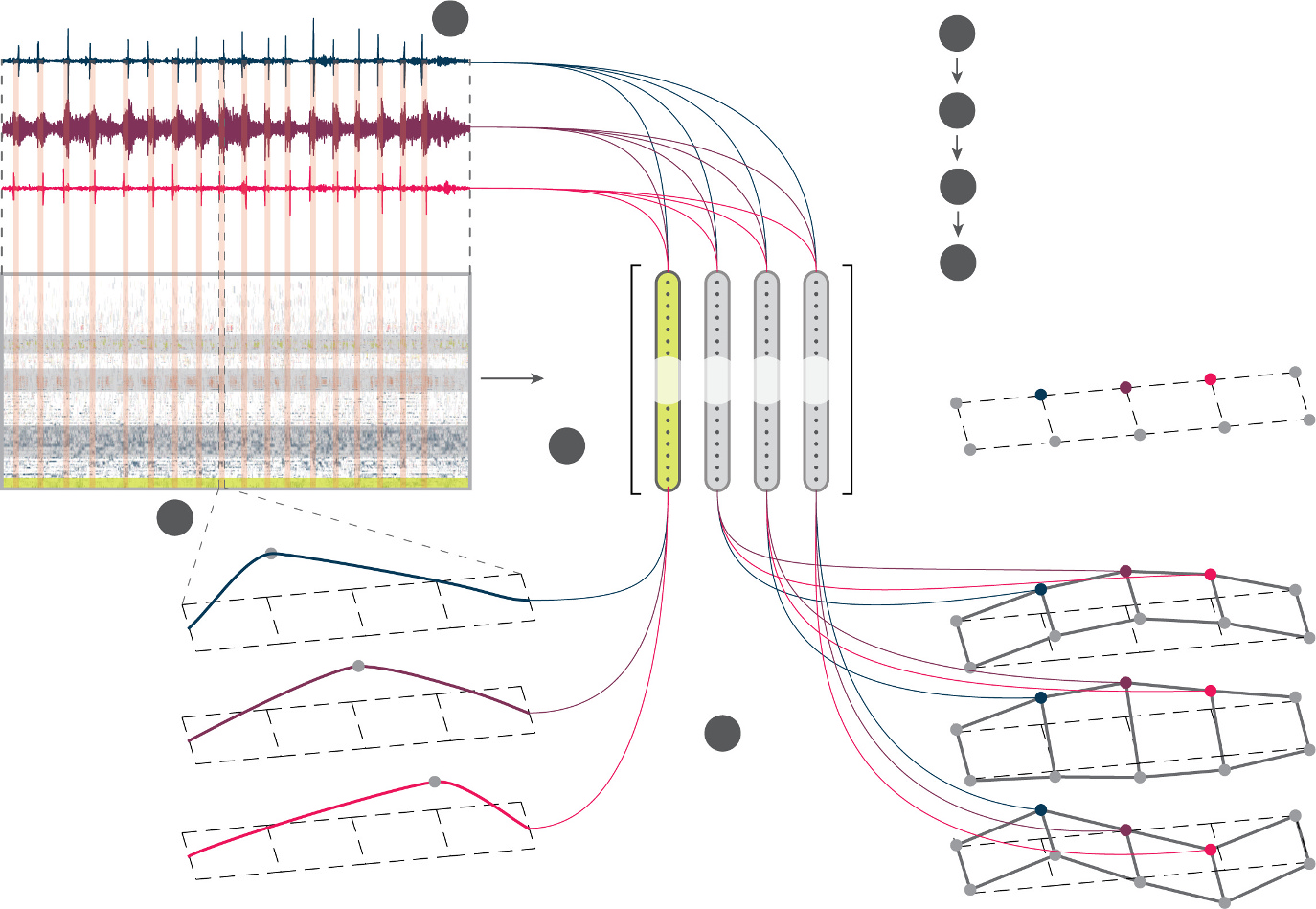
荷载进入桥梁跨径的时刻为$t= 0$，荷载离开桥梁跨径的时刻为$t=l/v$。平均影响线$\bar{h}^{(\zeta)}[z]$可以通过归一化（例如，归一化到所考虑区间内的最大值）来计算，以消除对车辆重量的依赖。考虑到在两个不同时间点识别出的平均影响线的基准状态和检测估计值，它们之间的（空间）逐点差异可作为损伤识别的密集特征。应注意，该特征的空间分辨率仅取决于$y_{i,0}[t]$的采样频率。图3展示了所提出过程的示意图工作流程：在收集信号并通过MAD构建滤波器组后——MAD可在给定的时间间隔（1）更新，选择分析窗口为车辆进入和离开桥梁跨径之间的时间间隔（2）；然后对加速度信号进行滤波（3）和归一化（4），以获得布设传感器位置处的模态参数稀疏估计值和密集曲率影响线。模态参数指$y_{r,p}[t]$的频率和幅值，可通过时域（例如，使用希尔伯特变换[6]或非线性能量算子[5]）或频域（例如，峰值拾取）轻松提取。这些已识别的密集和稀疏参数均可用于损伤识别。

需要注意的是，利用从解耦模态贡献中已识别的模态参数，可以获得在第i个布设传感器的位置施加力作用下的结构曲率的替代稀疏估计。实际上，该结构柔度矩阵的一种估计值是

$$
\mathbf{F} \cong \sum_{m=1}^{p} \frac{1}{\omega_m^2} \boldsymbol{\phi}_m \boldsymbol{\phi}_m^T \quad (33)
$$

其中，$p$为已识别的模态数量，$\omega_m$为第$m$阶固有圆频率。考虑在第$i$个位置具有单个非零元素的载荷向量$\mathbf{u}=[0,…,1,…,0]^T \in \mathbb{Z}^{r \times 1}$，结构的挠度形状为

$$
\mathbf{u} = \mathbf{Fp} \quad (34)
$$

然后可以使用有限差分法（例如中心差分）计算曲率。考虑多次车辆通过的平均曲率值可用于生成基准状态和检测特征，通过比较这些特征进行损伤识别。

3.2. 损伤识别

在常规实践中，结构损伤通过比较监测系统的两种状态来评估，即基准状态（此处称为“未受损”）和检测状态（可能已受损）。在本研究中，采用结构曲率作为损伤敏感特征。具体而言，我们假设曲率增量代表损伤，该损伤被建模为局部刚度损失。因此，通过影响线或模态参数计算得到的检测状态与基准状态之间的曲率估计差异，在此处被视为损伤指标。因此，损伤指标函数中的显著峰值表明存在损伤区域。

在一定假设条件下，曲率差值的幅值（为简便起见，此处称为“差值函数”）也可以损伤程度的代表性。下文将详细描述这些假设以及利用已识别影响线量化结构损伤的方法。

如前所述，对于简支梁，根据麦克斯韦‐贝蒂定理，当在某一给定位置$z= \zeta l$使用移动荷载计算影响线时，其曲线形状与在布设传感器的位置施加荷载时梁的挠度形状相同。在静定结构中，由于在某一位置$z= \zeta l$施加的未知集中荷载所产生的弯矩分布$M[z]$不依赖于结构刚度$EI[z]$，且具有三角形形状，并在$M_\zeta= M[\zeta l]$处达到最大值。在此情况下，基准状态和检测时间间隔内已识别的归一化曲率$h_u^{(\zeta)}[z]$与$h_d^{(\zeta)}[z]$之间的差值可表示为

$$
\Delta \chi(z) = h_d^{(\zeta)}[z] - h_u^{(\zeta)}[z] = \frac{M[z]}{C_d E I_d[z]} - \frac{M[z]}{C_u E I_u[z]} \quad (35)
$$

其中归一化因子$C_u$和$C_d$是

$$
C_u = \max\left(\frac{M[z]}{E I_u[z]}\right); \quad C_d = \max\left(\frac{M[z]}{E I_d[z]}\right) \quad (36)
$$

设$EI_u[z] = EI_u$在未损伤状态下随$z$保持常数

和A24高架桥的侧视图(b)[9])

将损伤视为在位置$z$处的局部刚度降低，并对损伤程度施加以下约束：

$$
E I_d[z] \geq \frac{M[z]}{M_\zeta} E I_u \quad (37)
$$

此条件假设归一化因子均相等

$$
C_u = C_d = \frac{M_\zeta}{E I_u} \quad (38)
$$

在这种情况下，损伤位置处的公式(35)变为

$$
\Delta \chi[z] = \frac{M[z]}{M_\zeta} \left( \frac{E I_u}{E I_d[z]} - 1 \right) \quad (39)
$$

因此，损伤梁的局部刚度可以被识别为：

$$
E I_d[z] = \beta[z] E I_u \quad (40)
$$

with

$$
\beta[z] = \left( \frac{M_\zeta}{M[z]} \Delta \chi[z] + 1 \right)^{-1} \quad (41)
$$

需要注意的是，一旦定位损伤（即在差值函数中找到峰值），$M_\zeta / M[z]$的比值很容易确定，且该比值不依赖于荷载大小，而仅取决于其位置（即布设传感器的位置）。此外，由于式(37)的假设，在远离布设传感器的位置处才能有效确定$\beta$的可靠值。另一方面，在靠近布设传感器的位置处，曲率函数的局部最大值仍可描述损伤位置，但其幅值不能代表损伤程度。

还应注意，对于用于识别影响线的低通滤波器给定的截止频率$f_l$，$\beta$的精度取决于车辆速度$v$和损伤的空间范围。具体而言，滤波信号的频率应足够高，以准确描述曲率的局部不规则性，即滤波信号周期应至多为车辆通过损伤部分所需时间的一半。换句话说，要准确识别损伤实体，损伤的最小空间范围为：

$$
D_{\text{min}} = \frac{v}{2 f_l} \quad (42)
$$

4. 应用

4.1. 结构识别：意大利A24高速公路

在本节中，将使用洛’阿奎拉大学于2019年2月至6月在A24高速公路高架桥上进行的实验研究期间收集的数据来测试提出的方法。意大利A24高速公路连接罗马与亚得里亚海，由于地形地貌复杂，沿线建有大量的高架桥。许多高架桥由单跨后张预应力梁组成，采用简支静定结构（图4）。如图5所示的梯形截面为2.3米高，并带有两个3.85米宽的悬臂翼缘。桥梁跨度由成对布置的空心截面桥墩支撑，桥墩中心间距约为40米。

使用了十个双轴力平衡加速度计(FBA)来记录桥面在交通激励下的响应，布置方式如图5所示。加速度计分为两个测量链，每个测量链由连接到Wi-Fi接入点的主记录单元引导，并通过全球定位系统进行同步。数据最初以200 Hz的频率采样，并使用了截止频率为40 Hz的抗混叠滤波器。

本文研究了三座高架桥，即切尔基亚拉、特米里诺和比塞利。采用了在竖直方向采集并以50赫兹下采样的1500秒加速度时间历史数据进行结构识别。在这些时间间隔内，一辆质量为1750千克、车轮轴间距为2.85米的汽车，如图5(c)所示，以30至60公里/小时的速度在桥梁上多次来回移动（本文中称为方向1和方向2），激励桥梁。

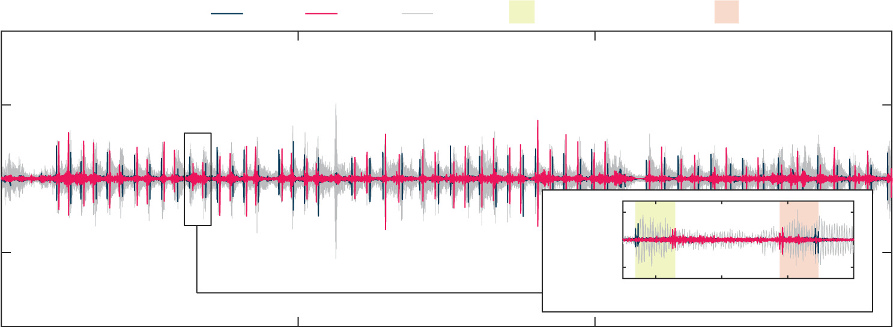
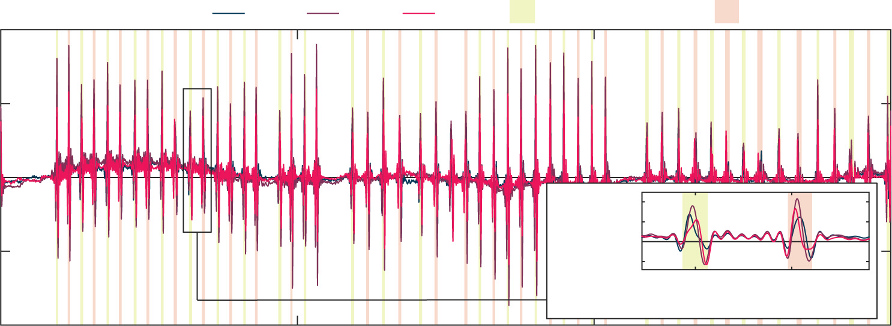
加速度计S1、S5、S6和S10位于伸缩缝附近。这些设备的记录用于选择汽车通过期间记录的信号区间，如图6所示，其中展示了在切尔基亚拉高架桥上采集的加速度信号。特别是，考虑到汽车的速度和几何尺寸，利用两个相近的加速度峰值（即时间间隔在0.2至0.4秒之间，由车轮通过伸缩缝时产生）作为触发序列来识别通过的汽车。具体而言，若传感器S1出现触发序列后，在6秒内传感器S5也出现触发序列，则表明汽车沿方向1行驶；相反地，若传感器S5出现触发序列后，在相同时间间隔内传感器S1出现触发序列，则表明汽车沿方向2行驶。本文中考虑了单车移动的情况。已识别的区间将用于评估准静态和动态结构特征。

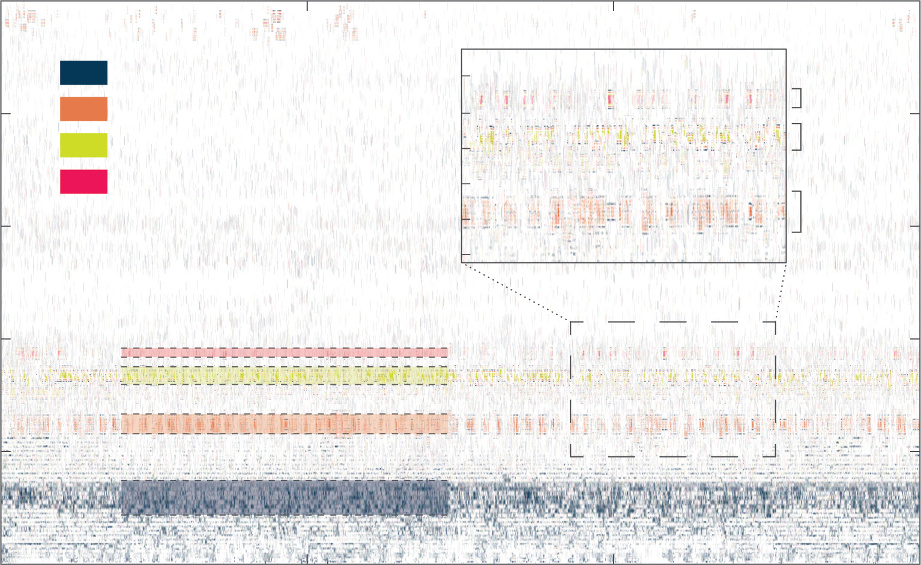
为了构建能够提取结构模态响应的滤波器组，将MAD应用于由全部10个记录通道组成的多变量信号。使用小波包变换（SWPT）进行初步信号分解，在第2.2.2节所述过程中采用Fejér-Korovkin 22小波函数。如该节所示，随后对相关的工作变形模式（ODSs）应用DBSCAN算法，识别出四种不同的振动模态（针对所有三座高架桥），并在时频平面上表示于图7中。在应用DBSCAN算法时，采用0.1的邻域搜索半径，并以欧几里得距离作为距离度量。在图7中，图7中显示了切尔基亚拉高架桥获得的$M_{k,t}$元素

和截面图(b)，改编自[9]以及车辆布置图(c)；尺寸单位为厘米)

两个尺寸，其中$t$为时间索引，$k$表示频率子带（重新缩放到0至25 Hz之间，即本研究中所用下采样信号的奈奎斯特频率）。在图7中，白色区域表示MAD值接近0，而超过θ阈值（此处选择为0.5）的元素被划分为四个不同颜色标注的簇。图的右上侧部分提供了放大视图，以便更好地显示与高阶模态相关的成分，这些成分通常更难识别。

用于提取已识别模态的等效带通滤波器按公式(26)计算得出。需要注意的是，在本研究中忽略了截止频率的时间依赖性，因为结构在短期内的结构行为不呈现变化的模态特征。在图7的左下部分，标出了用于提取模态贡献的四个频率段。

对于车辆通过期间识别出的每个时间区间，此处称为“采样区间”或简称为“样本”，通过将希尔伯特变换应用于解耦模态贡献来估计模态参数。通过希尔伯特变换计算得到的瞬时频率的平均值在图8中针对每个样本进行了展示。可以看出，已识别频率可能会表现出轻微变化。通过考虑在大量样本上计算的平均估计值，可以提高识别的鲁棒性。模态频率的平均值以及振型的平均幅值在图9中一并给出。需要注意的是，由于高架桥的几何形状相似，不同案例研究的模态参数也相似。此外，振型吻合良好与通过频域分解(FDD)获得的估计值一致，该方法是本研究中应用于持续时间为1500秒的整组信号的一种传统模态识别算法。

在此案例研究中，用于提取准静态特征的低通滤波器$b_0$的元素是基于由前两个小波滤波器组成的聚类滤波器来选定的，即

$$
b_0[\tau] = (g_{a,1} * g_{s,1})[\tau] + (g_{a,2} * g_{s,2})[\tau] \quad (43)
$$

在图10中，报告了Cerchiara高架桥传感器S2、S3和S4获得的低通滤波信号$y_{i,0}[t]$。高亮显示的区间是与通过的汽车相关的已识别样本。在放大视图中，可以观察到滤波信号的最大值与其采集位置一致。具体而言，

当汽车沿方向1行驶时，与S2相关的信号在采样区间的左侧部分达到最大值，而S4采集的信号在已识别区间的右侧部分达到最大值。相反地，在与方向2相关的区间中，峰值的顺序发生了交换。此外，在两种配置中，传感器S3的信号峰值均位于另外两个信号峰值之间。

从采样区间提取了曲率影响线的不同估计值，并在将时间变量$t$转换为空间变量$z=vt$之前，对与方向2相关的估计值进行了调换。图11中，每个案例研究和传感器位置的影响线估计值均以灰色显示。具体而言，每条灰色线表示在给定采样区间内由桥面两侧相对位置的两个传感器计算得到的影响线的均值（在每个图的右下角标出）。已识别影响线的平均值也以品红色标出，并与使用柔度矩阵计算的结构挠度曲率（仅在三个布设传感器的位置）进行比较，如公式(34)所示，该结果用蓝色表示。基于柔度的曲率是利用已识别的模态参数集合计算得到的，如公式(33)所示，图11中的结果为桥面两侧计算曲线的平均值。通常情况下，简支梁的曲率（或弯矩）影响线应包含两个线性段，在影响线评估点处达到最大值（本例中即为布设传感器的位置，由图11中的垂直虚线标出）。然而，由于所提出的方法对加速度时程应用了低通滤波器，导致有助于锐化影响线的高频成分被滤除，因此影响线的结果比理论结果更平滑。还应注意的是，由于中心差分法的限制，在此应用的传感器布局下，使用基于柔度的方法只能计算出三个曲率点。通过基于柔度的过程获得的结果与理论结果略有差异，但与密集的通过提出的方法获得的特征。尽管估计值与影响线的理论形状存在差异，但所示结果可有效用于结构健康监测流程中结构异常的定位。这一方面在本文下一节介绍的数值案例研究中进行了展示。

4.2. 损伤识别：数值基准

本文分析的第二个案例研究是一个简支梁的数值模型，其结构特性与上一节分析的高架桥相似。具体而言，梁的长度为40米，横截面建模如图5(b)所示，整体抗弯刚度为$EI= 105.96 \cdot 10^6$ kNm²。所有振动模态的模态阻尼均假定为5%。三个单轴加速度计已被模拟，用于采集图12所示位置处竖直方向的加速度。本案例研究中使用了一排传感器，因为该梁被建模为一维结构。

为了模拟第3节中提出的损伤识别方法的应用，考虑了四个损伤位置，形成了表1中总结的七种损伤工况。具体而言，在L1、L2和L3段内模拟了单个或多个局部损伤（用于模拟车辆在桥梁下方通过时产生的冲击或裂缝区域）。另一方面，D位置模拟了一种弥散性刚度降低（例如由于剥落引起），并用于生成三种不同严重程度的损伤工况。

在此案例研究中，移动荷载被建模为一个单一的力，以恒定速度穿过结构（从左到右，如图12所示）。

在初步分析中，影响线已通过处理以100 Hz采样的纯净加速度信号，该信号是在一个时间段内采集的，代表移动荷载在梁上通过的过程。具体而言，图13展示了通过低通滤波器得到的曲率影响线（归一化至最大值），该低通滤波器由7层小波包变换的前两个分量组成（截止频率为0.78 Hz），并使用Fejér-Korovkin 8函数生成。针对每个传感位置（在每幅图的右下角标明）和损伤状况所获得的结果以实线绘制，而未受损状态与各损伤情况之间归一化影响线的差异则以虚线表示。本研究考虑了不同的车辆速度。特别是，图13(a)和(b)是模拟车速为15米/秒时车辆通过的情况所得结果，此时位置被离散化为264个点。另一方面，图13(c)显示了使用3米/秒车速时获得的结果，此时位置被离散化为1332个点。需要注意的是，每个结果仅基于单个传感器进行分析得出。

，滕佩里诺(b)，和比塞利(c))

位置 位置 位置
局部损伤 未受损 DC1 DC2 DC3
S1 S2 S3 0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 66 132 198 264
-0.5
0
0.5
1
Curvature
-0.05
0
0.05
0.1
Difference
0 333 666 999 1332
-0.5
0
0.5
1
Curvature
-0.1
0
0.1
0.2
Difference
0 333 666 999 1332
-0.5
0
0.5
1
Curvature
-0.1
0
0.1
0.2
Difference
位置 位置 位置
位置 位置
0 333 666 999 1332
-0.5
0
0.5
1
Curvature
-0.1
0
0.1
0.2
Difference
弥散损伤 未受损 DC4 DC5 DC6
弥散损伤 未受损 DC1 DC5 DC7 局部损伤
位置
(a)
(b)
(c)
S1 S2 S3
S1 S2 S3
0.049 0.050 0.042
0.026 0.050
0.076
0.058
0.157
0.065
0.157

，滕佩里诺(b)，和比塞利(c))

在局部损伤情况下，差分函数的明显局部最大值（用圆圈标出）均靠近真实损伤区域，且与车速无关。然而，使用慢速车辆可识别出更尖锐的峰值。在此情况下，还可识别出多处损伤的存在（工况DC7）。类似地，在弥散损伤附近始终能识别出差分函数的高值；而在慢速车辆情况下，损伤指标受动力效应的影响较小，从而实现更准确的损伤定位。

在确定损伤区域的位置后，可使用公式(41)对刚度损失进行损伤量化。利用传感器S1识别出的数值（明确列于图13中）所得的损伤量化结果以$(1 - \beta) \cdot 100\%$的形式显示在图14中。需要注意的是，根据公式(42)，对于车速为15米/秒的车辆，能够被正确量化的最小损伤其延伸长度$D_{\text{min}}$为9.6米（考虑对应前两个小波分量的低通频率0.78赫兹）。实际上，图14(a)中报告的已识别值低估了损伤程度，因为损伤区间（2米）远小于$D_{\text{min}}$。另一方面，对于相同的车速，图14(b)中所示弥散损伤对应的损伤程度值更为准确，特别是在低损伤水平时。最后，当车速为3米/秒时（此时$D_{\text{min}}$为1.9米），局部损伤工况下的损伤程度也可被正确识别。

尽管在受控环境（即恒定速度和精确路径）下可使用以3米/秒行驶的特定检测车辆并配备高灵敏度加速度计，但较快速度的车辆更能代表普通交通条件，其中噪声源通常不可忽略。因此，在进一步分析中，通过引入标准差等于采集的加速度标准差50%的显著高斯白噪声成分，对记录的时间历程进行了污染。这种显著的噪声水平代表了多种现象，包括仪器噪声、轻微的非恒定车速以及非直线路径。在此情况下，考虑了未受损状态及从DC1到DC6每种损伤状况的100个样本区间，以从归一化样本估计值计算平均影响线，然后用于计算损伤指标（即差值函数）。该分析的结果如图15所示。具体而言，该图显示了每个样本获得的影响线（细线）及其平均曲线（粗线），以及每个传感器位置（S1、S2和S3）和损伤工况（DC1到DC6）的差分函数（虚线）。在这种情况下，差分函数受到噪声干扰，导致损伤定位变得困难。然而，通过组合差分函数，即在每个空间位置对其求和，可以改善损伤定位效果，如图16所示。

在噪声较大的环境中，差值函数的峰值也可能由动力效应引起。在这种情况下，尽管模态参数无法识别损伤的确切位置，但可用于识别损伤区域，其中差值函数的峰值可能与实际损伤相关。图17显示了通过模态柔度法（如第3.1节所示）获得的平均曲率（基于100个含噪声样本计算）所得到的差分函数。具体而言，考虑了三种荷载向量$\mathbf{u}$，其非零荷载元素分别位于位置S1、S2和S3，如各图右下部分所示。在所有情况下，差分函数的高值均出现在传感器S2和S3之间。因此，可以判断

从位置0和66之间的影响线获得的差分函数中的局部峰值（图16(a)）可能由动力效应引起，与实际刚度损失无关。

使用在传感器S1处识别的影响线，在噪声环境下进行损伤量化所获得的结果如图18所示。正如预期，局部损伤状态未能被正确量化。此外，弥散损伤状态的结果精度低于图14中报告的结果。然而，图18(a)仍显示出所有局部损伤状态的已识别值相似，且图18(b)正确地报告了由于逐渐增大的损伤程度引起的增长趋势。

5. 结论

本文提出了一种针对简支钢筋混凝土高架桥的结构健康监测新方法，能够以简单且集成的方式同时识别动态和准静态参数。具体而言，模态置信分布（MAD）结合聚类小波带通滤波器，适用于从受交通激励作用的结构中提取模态参数的稀疏估计。该方法已成功实现了对三座高架桥振型和固有频率的精确识别。此外，准静态特征能够实现对结构行为的密集描述少量加速度计。通过额外的小波低通滤波器提取的低频信号分量所获得的曲率影响线，确实能够代表在布设传感器的位置施加竖向力时结构曲率的实际状态。利用这一事实，已提出一种基于曲率的损伤敏感特征，同时避免了传统方法中对识别出的振型进行二阶微分所带来的近似误差。所定义的损伤指标为曲率影响线之差，已证明能够利用稀疏传感器网络的加速度计以较高的精度实现损伤定位。此外，该指标可反映损伤程度，且无需了解结构质量信息或使用有限元模型。数值案例研究的结果表明，在使用极稀疏传感器网络（例如仅一个传感器）时，噪声可能会影响识别过程的结果。然而，通过在多个传感位置将检测影响线从基准状态中减去所得到的累积差值函数，显著提高了损伤定位的准确性。此外，模态特征所提供的信息有助于排除由动力效应引起的损伤指标峰值，从而避免误判为实际损伤。所提出的流程取得了令人鼓舞的结果，尤其适用于在区域层面采用低成本稀疏传感方案进行结构健康监测的应用。