线代九讲_矩阵运算

第三讲 矩阵运算

知识点

求An的五种方法

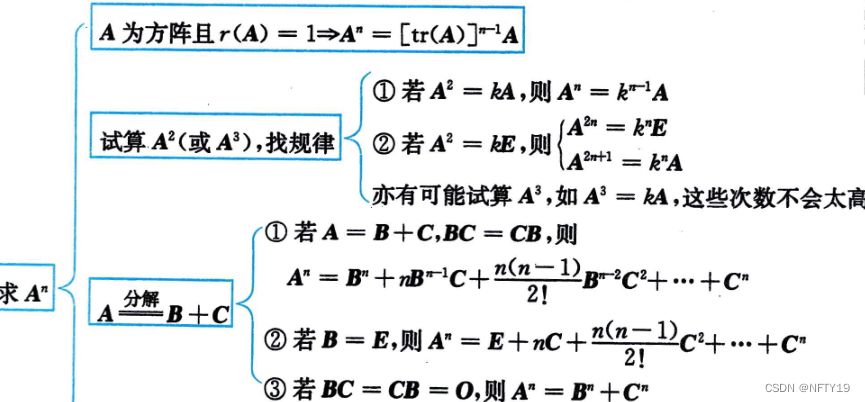
①首先看其秩是否为1
②看其特征值是否好求（是否为三角矩阵…）
③看能否拆成（单位阵和一个简单的矩阵）或（乘积为0的两个矩阵）的和
④尝试找规律

伴随矩阵（直接背）

①注意伴随矩阵元素（各个代数余子式）的位置
②公式里要小心②④⑦

求逆矩阵（各两种方式）

注意抽象型求逆矩阵的两种思路

分块矩阵

分块矩阵重点：


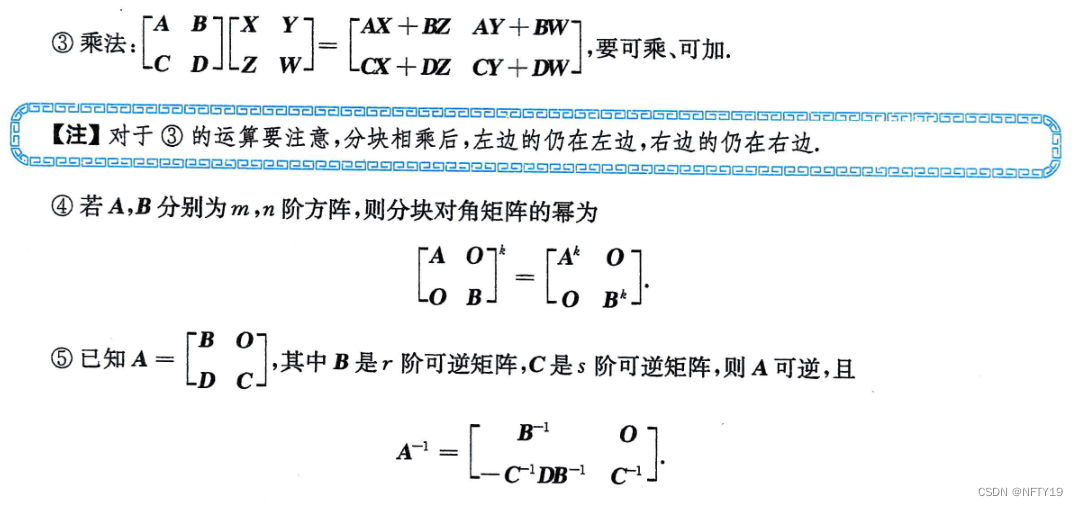
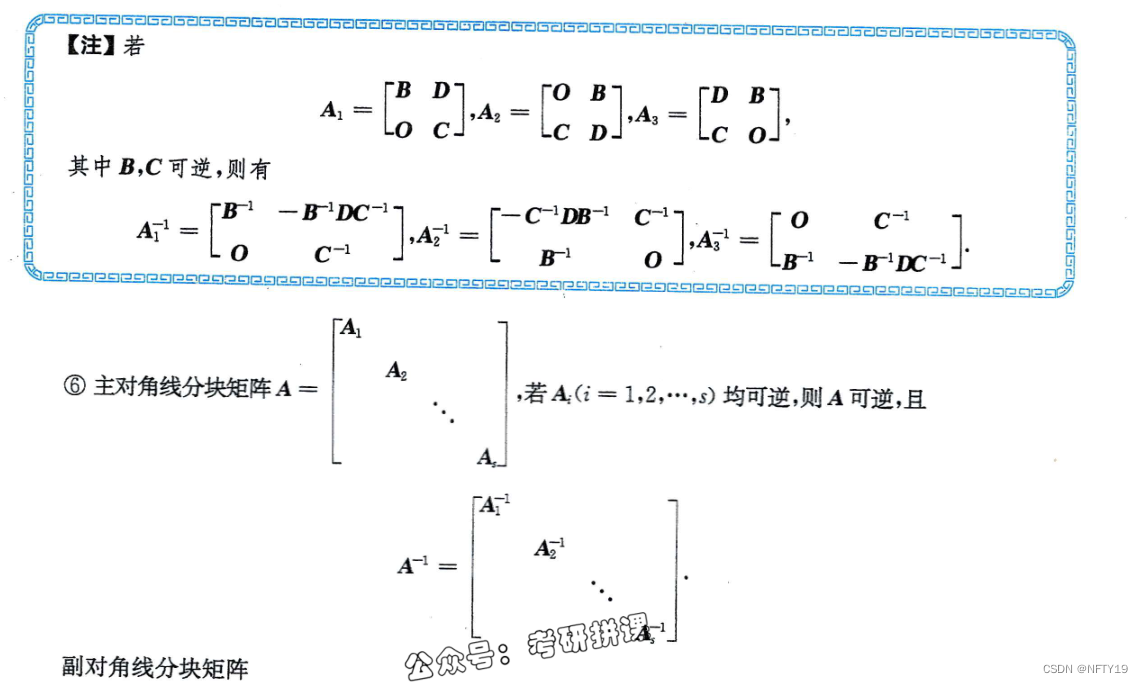
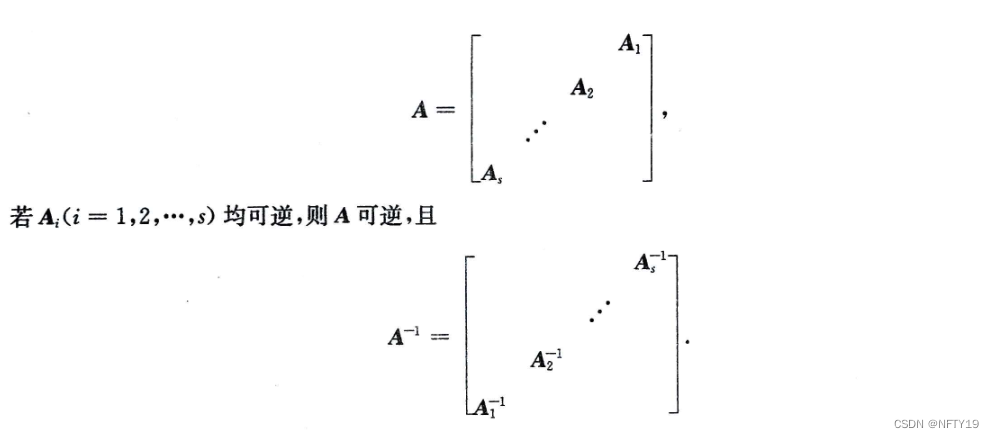
副对角线分块矩阵的逆矩阵，对角线元素位置要对调

重点题型

1

类比的思想（直接用一阶矩阵类比）

2

矩阵方程变换（本体重点在于A*与A逆之间的转换）

3 易错题

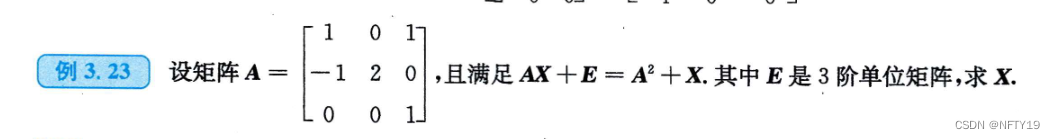
在使用矩阵方程的时候，乘以逆矩阵的时候，一定要注意矩阵是否可逆。
若不可逆的时候，就可以使用方程组(按列分块)

4

这种完全无法化简的题目，就可以考虑待定系数法（而且是二阶）
解：

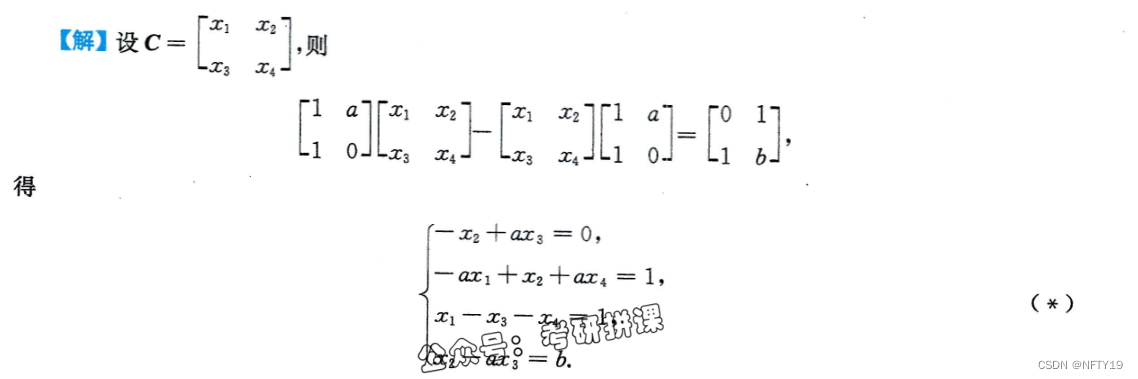
5（算）

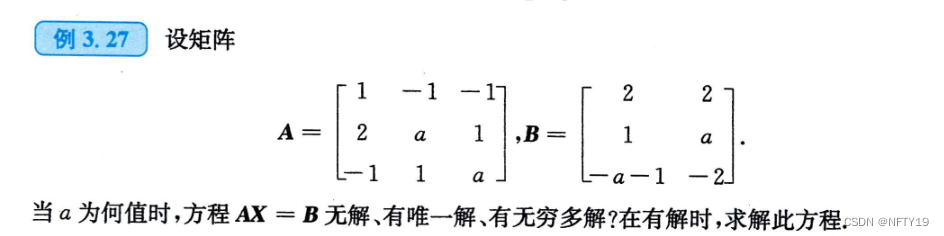
直接当成方程组来解。

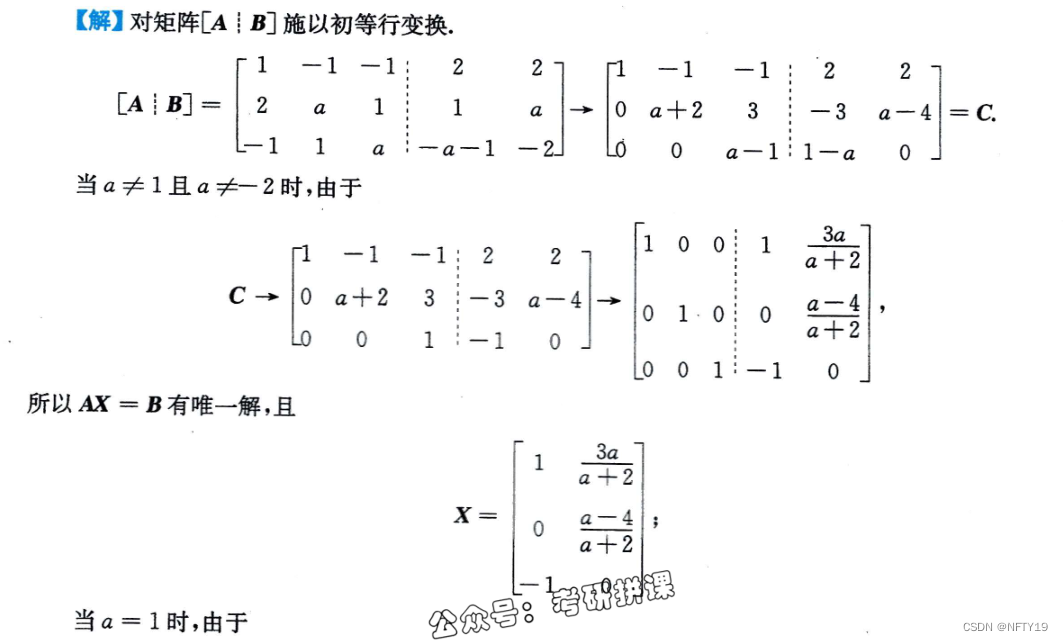
67（证明矩阵可交换）

主要就三种思路（凑成下面三种形式）：
①A A* = A* A
②（E - A）（E + A） = （E + A）（E - A）
③AB = E = BA

8（难）

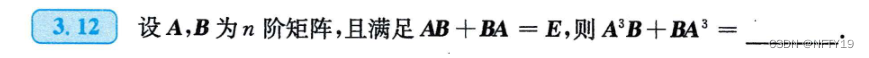
考虑用构造矩阵方程组来做：

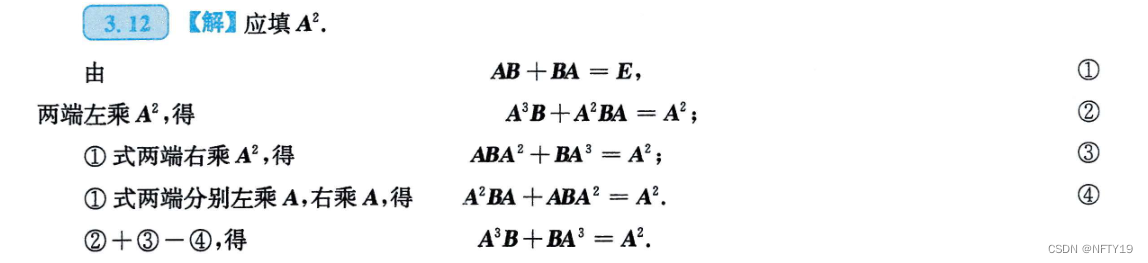
9（难）

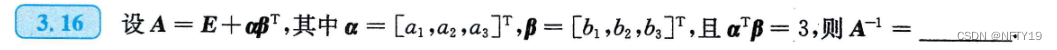
通过题目所给条件，构造矩阵方程，目的是得到关于A的方程式（以此可以算出A逆）

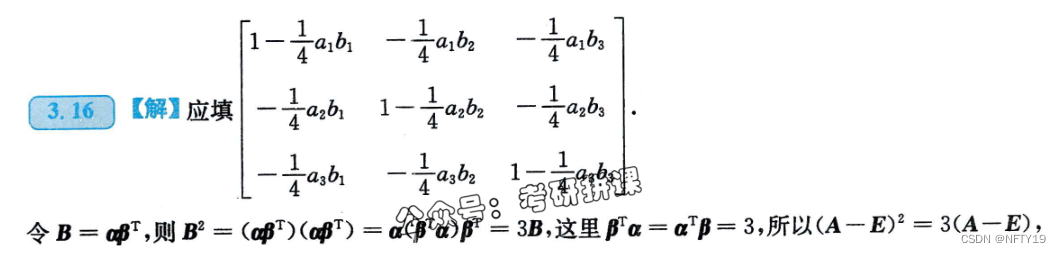
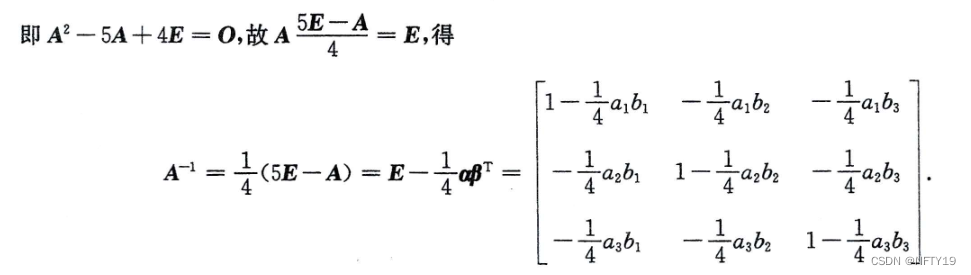
10（难）

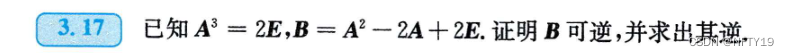
本题就是经典的求逆矩阵的第二种方法。将要证明的矩阵，拆成几个可逆矩阵的乘积。分别求出这几个可逆矩阵。

11（必会）

这种题不要去猜，要去用初等矩阵表示。经行矩阵运算。