贝叶斯决策建模

贝叶斯决策建模

先验分布

根据先验信息所确定的概率分布叫先验分布，获得先验分布是贝叶斯分析的基础。决策中先验分布的获得具有高度的主观性。

先验假设

为使先验分布估计规范化，需要做一定的假设。

• 连通性假设：指事件A和事件B发生的可能性是可比的
• 传递性假设：若对事件A、B、C，有p(A)>p(B), p(B) > p( C), 则p(A)>p( C)。
• 部分与全体：部分与全体关系假设：若事件A是事件B的一部分，则p(B)≥p(A)。

先验分布估计

• 比较法1-离散型（对事件发生的各种状态加以比较确定相对似然率）
• 打赌法（离散型）
• 直方图法（适合于自然状态$\theta$在实轴某个区间连续取值）
• 区间对分法（分位点法）-连续型
• 分布函数法

效用函数

效用就是偏好的量化值。决策的目标就是使期望效用极大化

效用函数的构造

• 离散型：构造决策树
• 连续型：则可通过分析u©的若干特征值，求出特征点的效用后再连成光滑曲线。

决策准则

决策树表示法

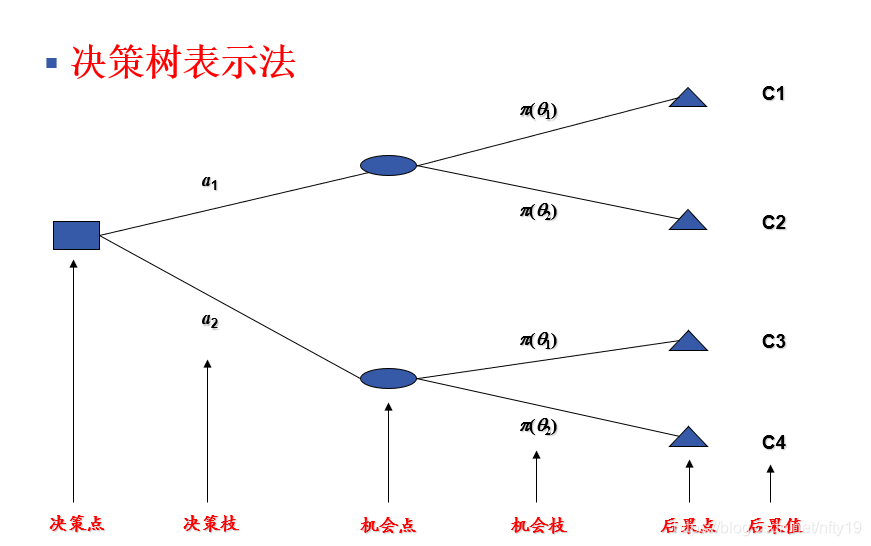
贝叶斯准则：期望效用最大或期望损失最小。

---

贝叶斯决策

​ 贝叶斯决策就是在不完全情报下，对部分未知的状态用