本文探讨了线性代数中向量组的相关概念，包括线性相关性判断、向量组等价、矩阵等价的条件。重点介绍了如何确定向量组的极大线性无关组、计算秩以及特殊情况下的向量表示。同时，讲解了通过定义证明矩阵乘法的性质，并分析了四个3维向量线性相关性的证明方法。内容适用于线性代数的学习与教学。
第六章 向量组
知识点
线性相关性判别
向量组等价（同维；三秩相等）★★★
类似于同解方程：
三秩相等、互相线性表出、单方线性表出+两秩相等
矩阵等价（同型；两秩相等即可）★★★
重点题型
1
必会题
2 极大线性无关组
3 秩
特殊值（用定义）
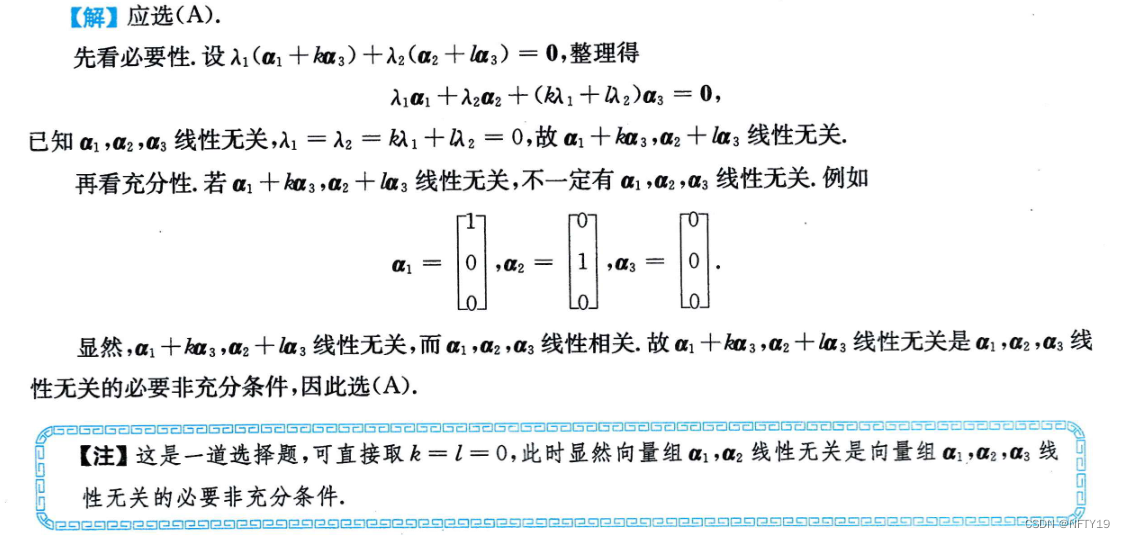
4
通过必要条件找到线索。得到参数的值后，带入验证。
带入验证
5
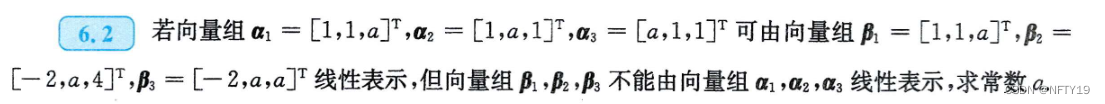
某三维向量，不能由向量组表示，表明该向量组秩小于3.
6
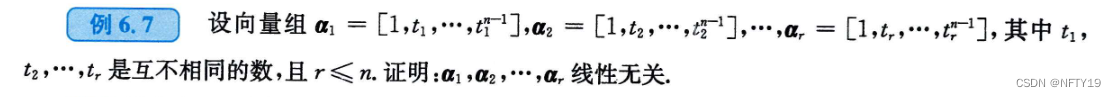
①写出定义
②构造齐次线性方程组
③证明方程组只有零解
当r<n时，可以降维构造分量线性无关。
7（证明）
两矩阵相乘，可以先构造定义式，然后构造所给的相乘式。
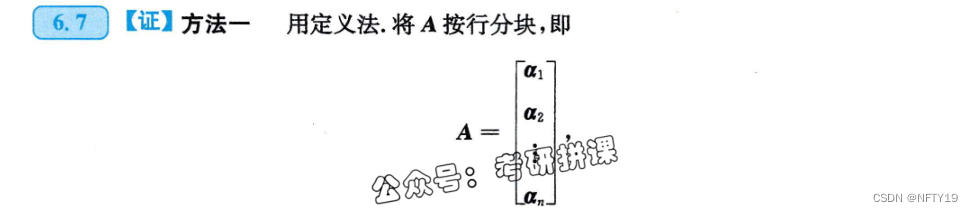
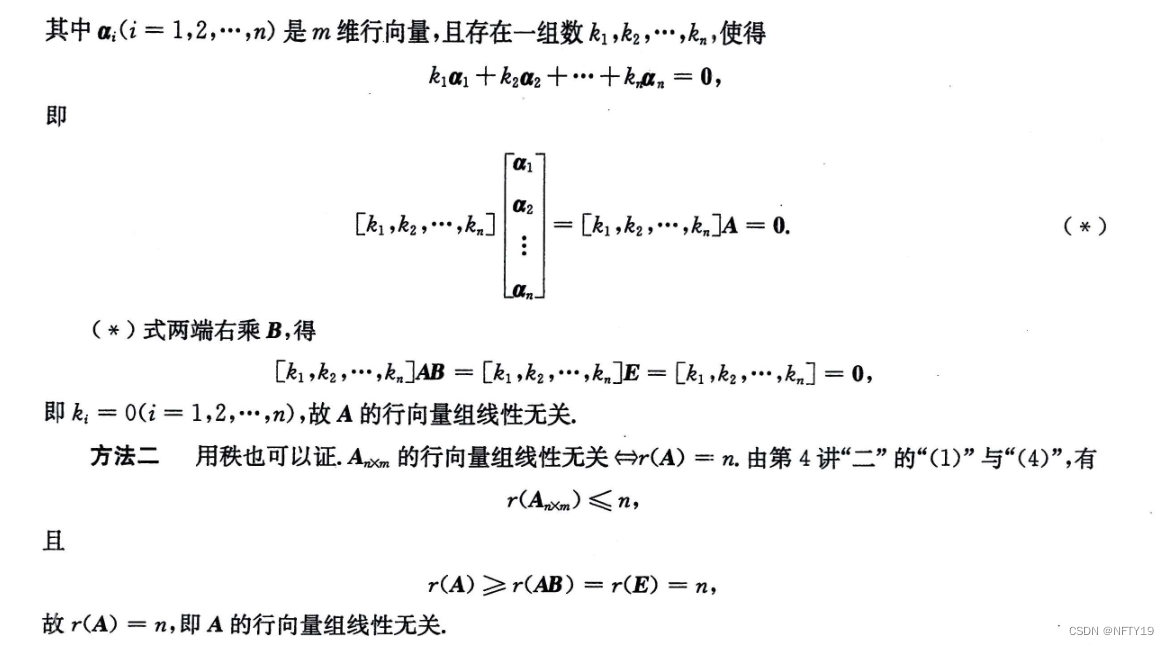
8
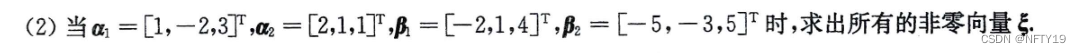
主要考察的点在于 四个3维向量必线性相关。（故可以构造定义式）
扫一扫
1500
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
