一元函数微分学
高数十八讲_第三讲
1 概念题

题目中很明显能看出题目只给了极限值,并没有表明在该点的值。故其不一定连续。
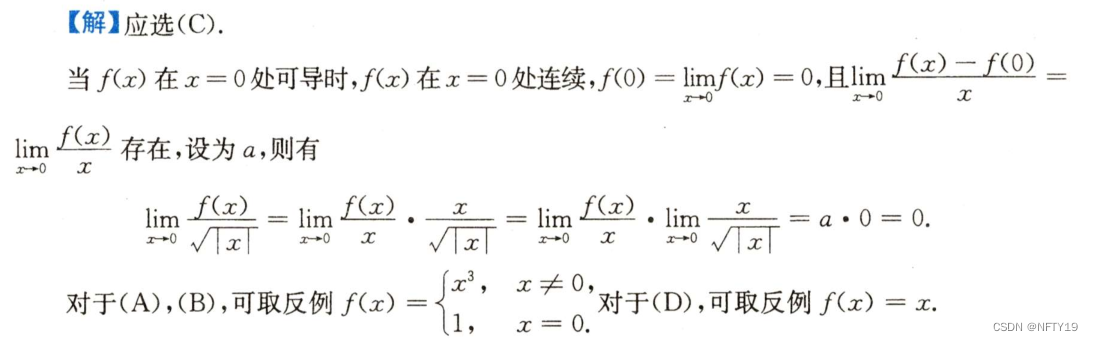
2 导数定义(放缩)

这题有点难度,是一个区间列(对函数进行操作的时候,首先就要确定一个小的范围,再操作)。但是看到这个区间,能不能反应过来放缩?

3
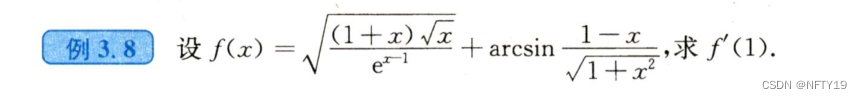
直接求导会不会有点麻烦?用定义求导会不会也不太方便?
这个技巧就非常好

4
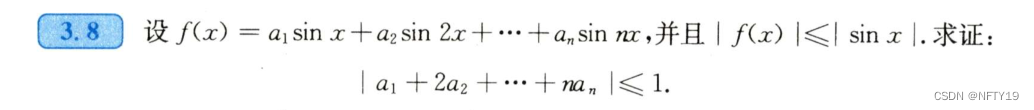
看到证明的左边,能想到什么?
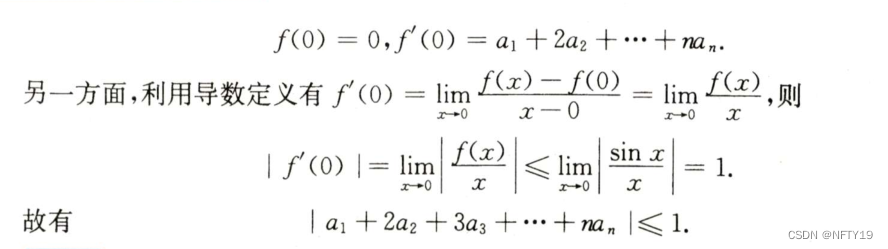
高数十八讲_第四讲
高阶导数


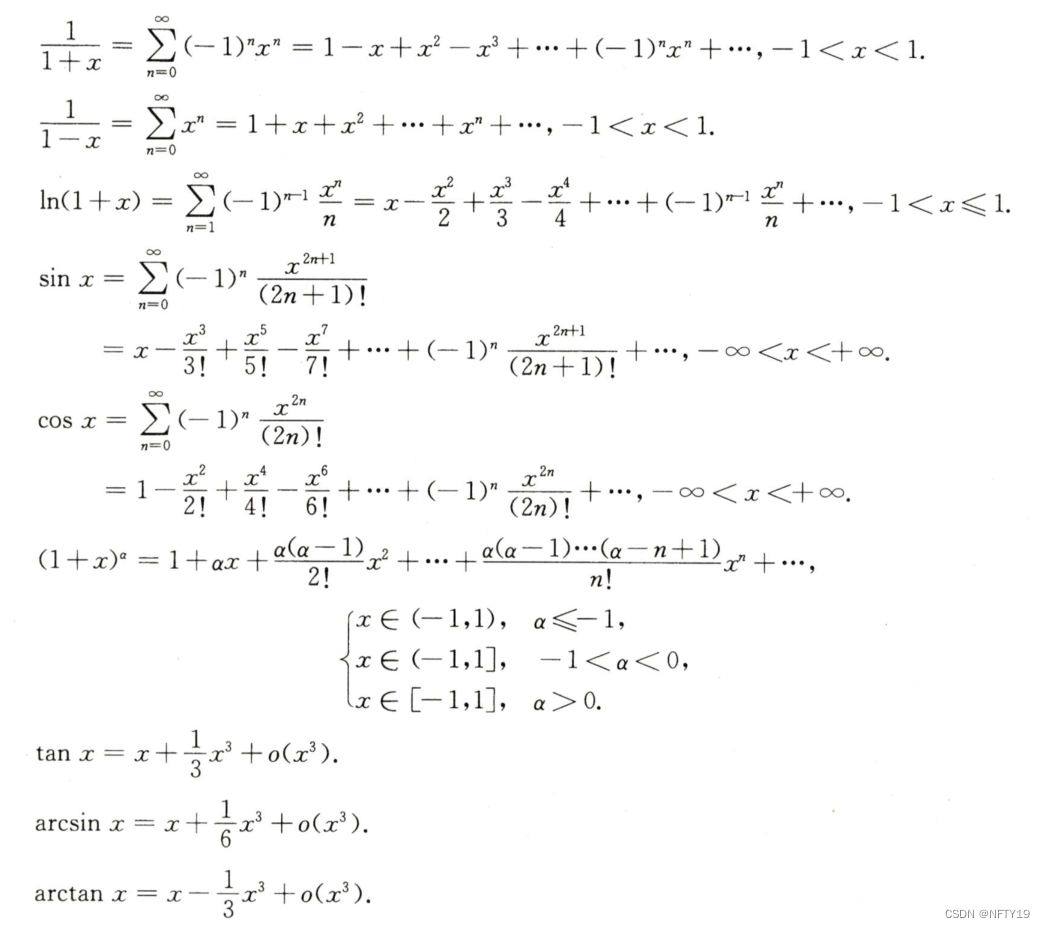
1易错题
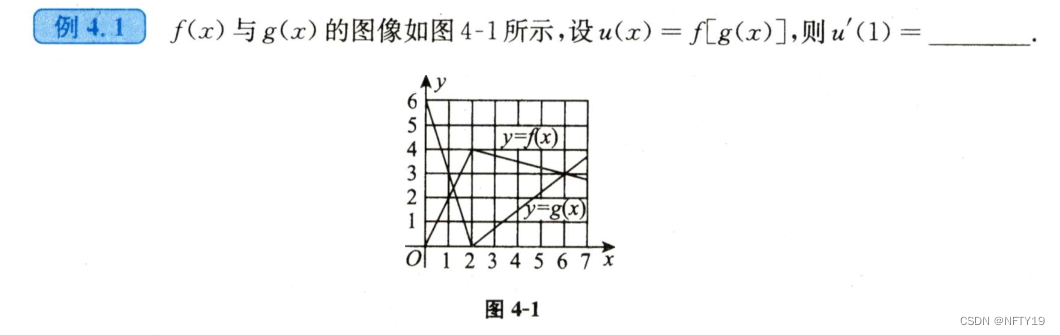
复合函数算导数的时候,要看清 内部函数和外部函数 分别具体在哪里求导
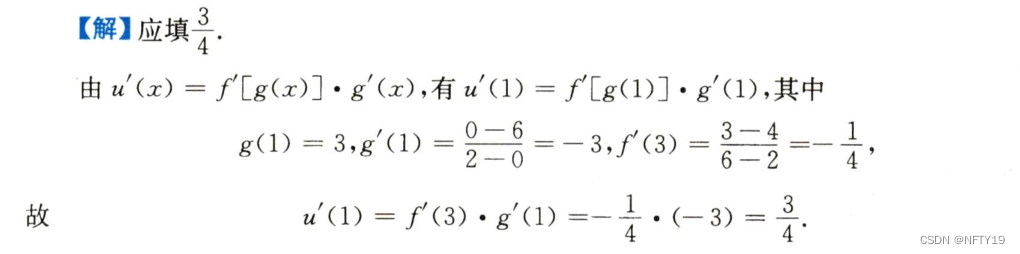
2套路题
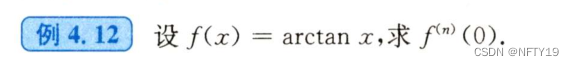
特定的套路

3 重点
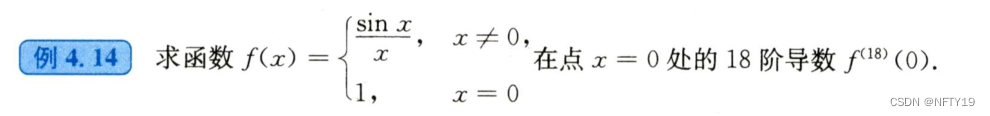
这种分段函数的导数,一定要搞清楚!

解:
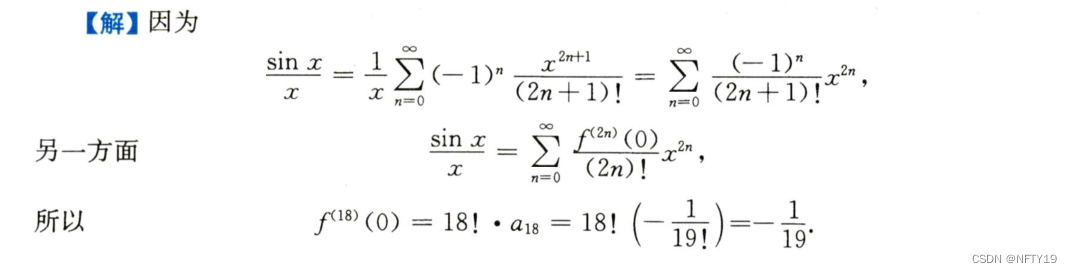
4 ▲
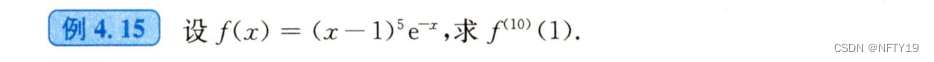
这题对于不在0点处展开,需要会(直接将表达式带入麦克劳林公式即可)

1000题强化训练第三章
1
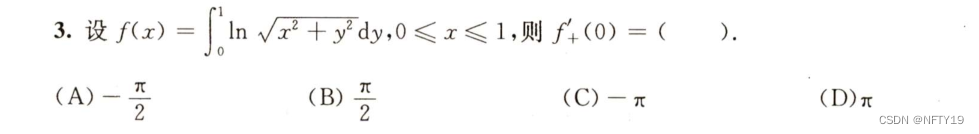
先求出函数表达式,再求导
2

这题一定要注意的是,三次根号x本身在0处不可导

1000题强化训练第四章
1
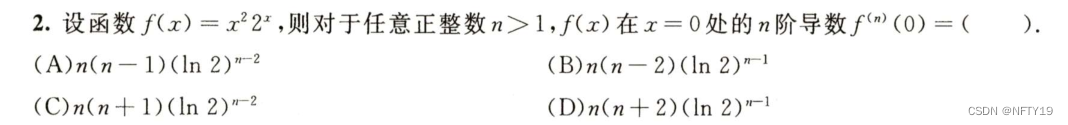
典型题(两种思路),
①x=a处泰勒展开,通过直接法、间接法,比较系数(注意有个k!)
②莱布尼茨公式,直接当成两个函数相乘(类似与二项式展开的形式)
解:

2

这种题一定不要怕麻烦,一阶一阶求。

1000题巩固提高第四章
1

本质上还是换元,将微分方程转化。解:

2
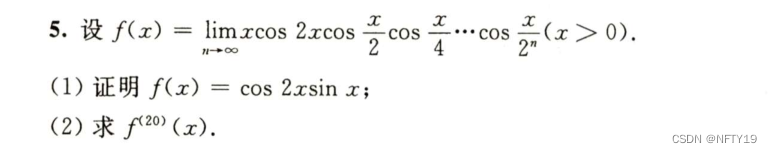
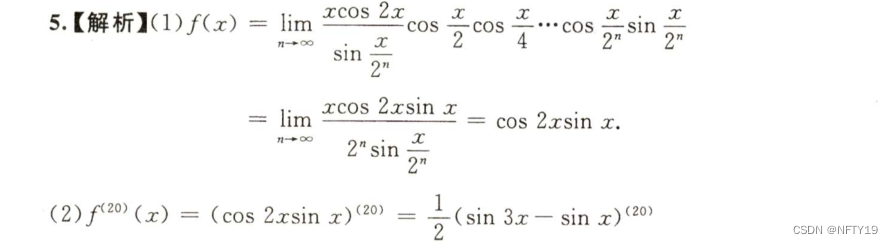
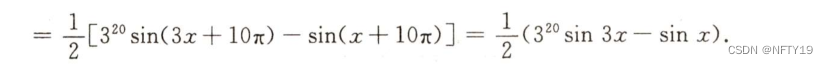
3
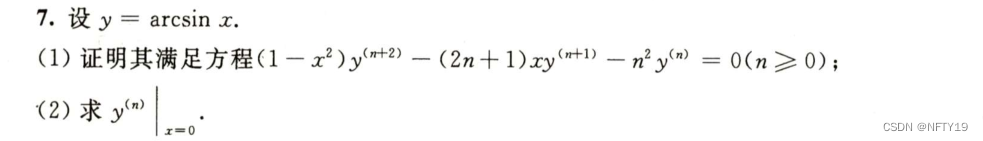
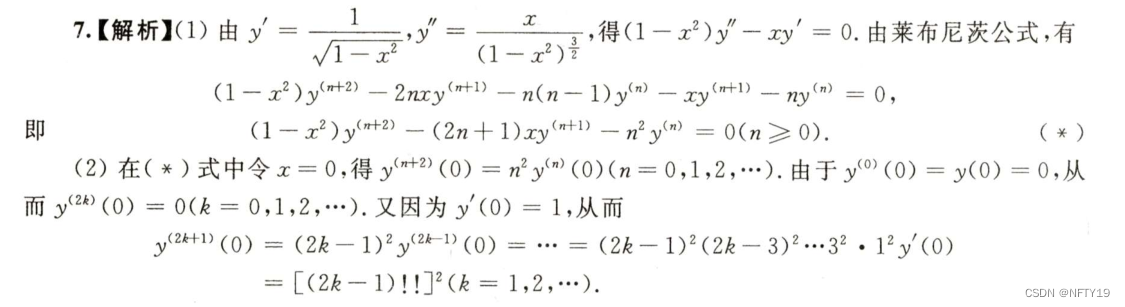
 微积分技巧与高阶导数解析
微积分技巧与高阶导数解析





 这篇博客深入探讨了一元函数微分学中的关键概念,包括极限、导数定义及其应用。讲解了如何处理区间列和使用放缩技巧求导,特别强调了分段函数导数的确定。此外,还介绍了泰勒公式在证明和求解中的作用,以及高阶导数的重要性。同时,提供了多种解题策略,如泰勒展开、莱布尼茨公式等,并提醒读者注意特定类型的函数(如三次根号x)在某些点可能不可导。博客通过丰富的例题和解题步骤,帮助读者巩固和提升微积分技能。
这篇博客深入探讨了一元函数微分学中的关键概念,包括极限、导数定义及其应用。讲解了如何处理区间列和使用放缩技巧求导,特别强调了分段函数导数的确定。此外,还介绍了泰勒公式在证明和求解中的作用,以及高阶导数的重要性。同时,提供了多种解题策略,如泰勒展开、莱布尼茨公式等,并提醒读者注意特定类型的函数(如三次根号x)在某些点可能不可导。博客通过丰富的例题和解题步骤,帮助读者巩固和提升微积分技能。
















 565
565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








