Comsol三维晶体轴压模拟：基于三维Voronoi算法的奇妙旅程

原创于 2025-12-20 17:30:00 发布 · 464 阅读

CC 4.0 BY-SA版权

文章标签：

comsol三维晶体轴压模拟基于三维voronoi算法三维泰森多边形晶格分布为comsol模型

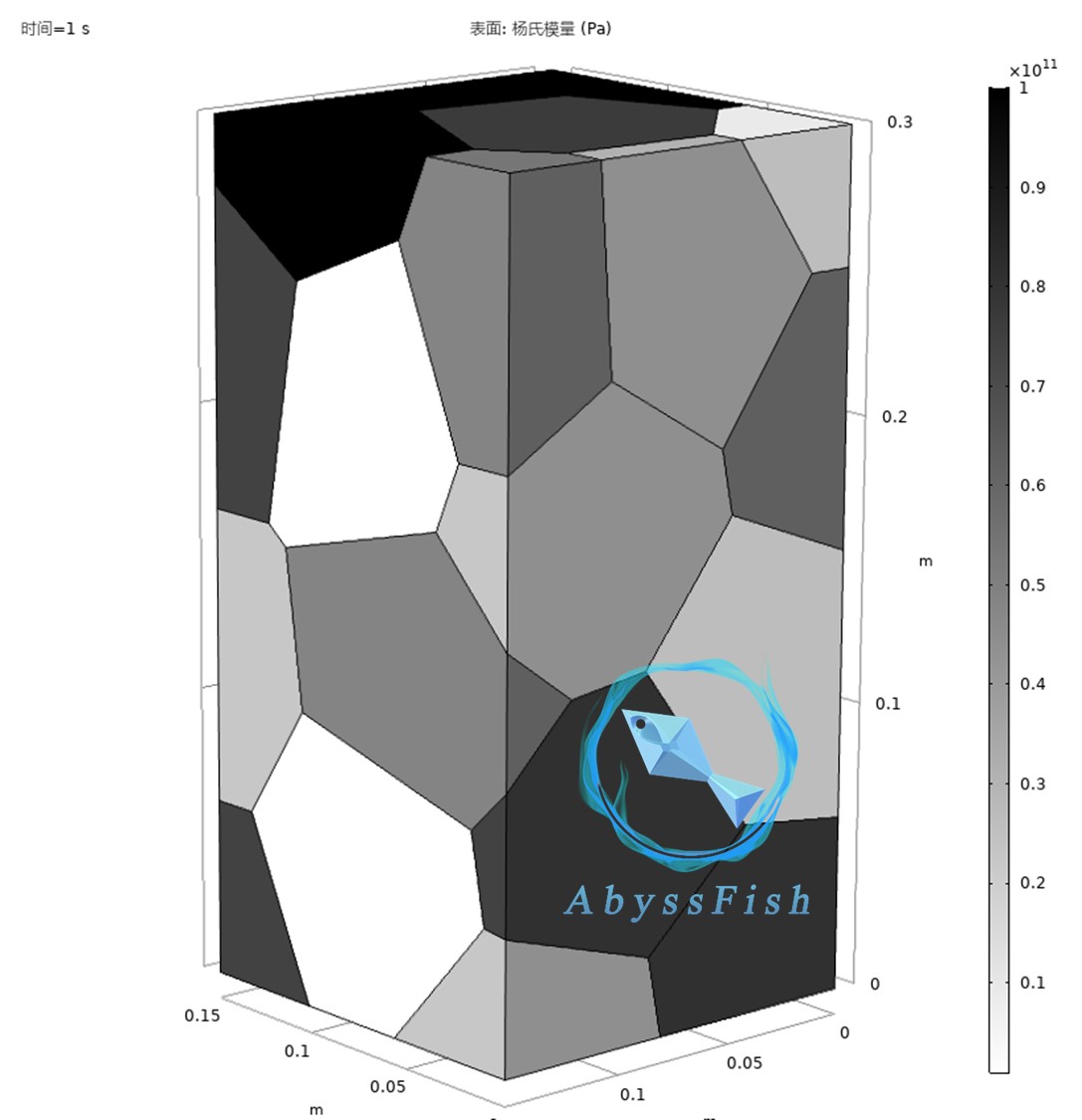
在材料科学和力学研究领域，对晶体在轴压下的行为模拟有着至关重要的意义。今天咱就来唠唠基于三维Voronoi算法实现三维泰森多边形晶格分布的Comsol三维晶体轴压模拟。

三维Voronoi算法是啥呢？简单说，给定空间中的一组离散点（种子点），它能将整个空间划分成多个区域，每个区域内的点到该区域对应的种子点距离最近。这就形成了所谓的三维泰森多边形晶格分布，在晶体模拟中，这种分布可以很好地模拟晶体内部复杂的微观结构。

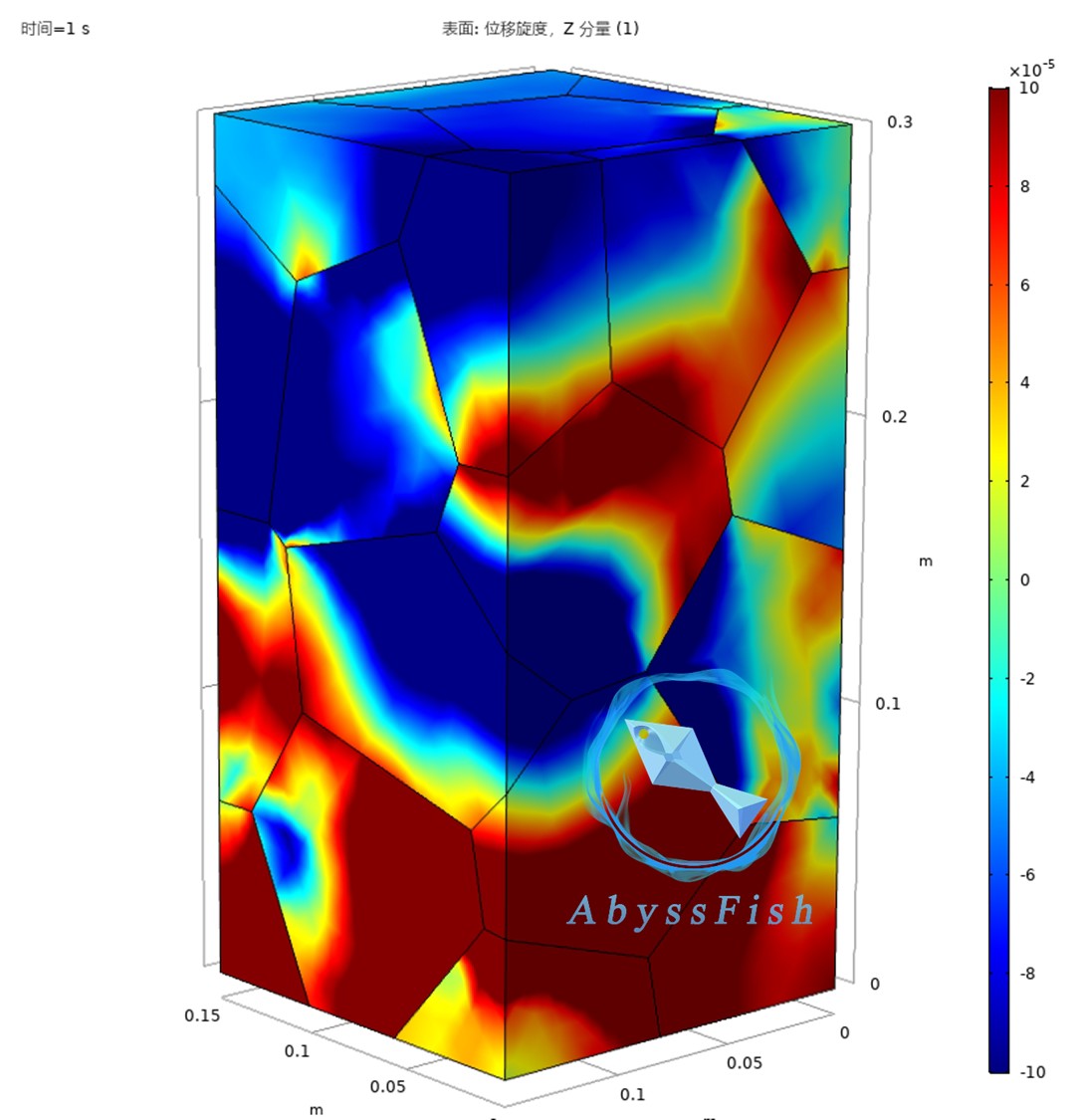
想象一下，这些种子点就像晶体中的原子初始位置，通过Voronoi算法划分出的区域，就类似每个原子周围的势力范围。代码实现上，以Python为例，我们可以用scipy库中的scipy.spatial.Voronoi来构建基本的Voronoi图：

import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d
# 生成一些随机种子点
points = np.random.rand(10, 3)
vor = Voronoi(points)

这里我们先导入所需的库，然后生成了10个三维空间中的随机点作为种子点，接着用Voronoi函数生成Voronoi对象。虽然这只是二维展示的相关代码，但能让大家对算法的基本使用有个概念。在实际三维模拟中，我们需要进一步处理这些数据以适配Comsol模型。

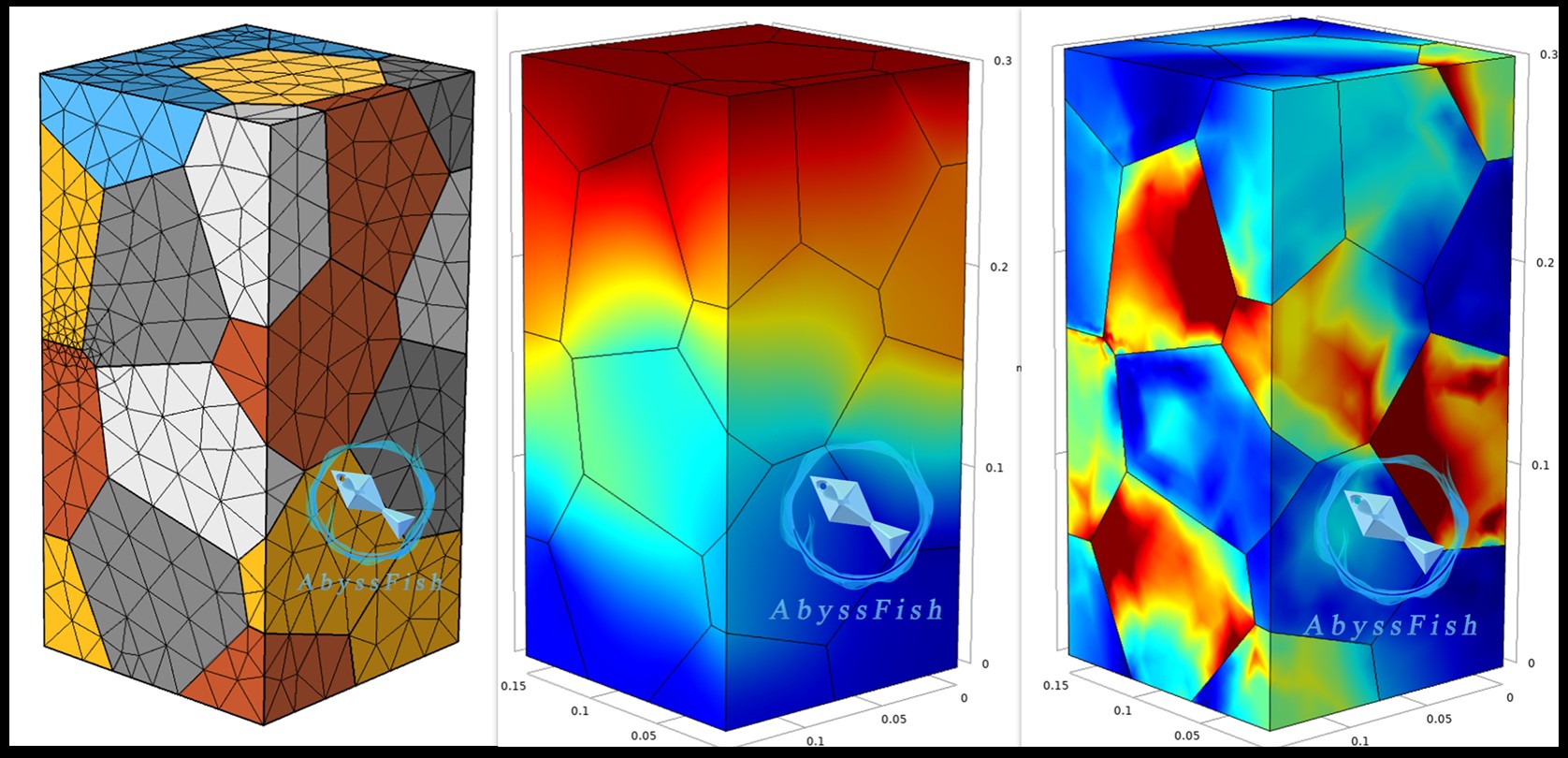
在Comsol中，我们要基于上述生成的晶格分布来构建晶体模型。首先，在几何模块中，我们需要根据三维泰森多边形晶格分布的坐标数据来创建几何结构。这可能需要一些数据导入和处理技巧。假设我们已经将Voronoi算法生成的晶格顶点坐标导出为一个文件（比如.txt格式）。

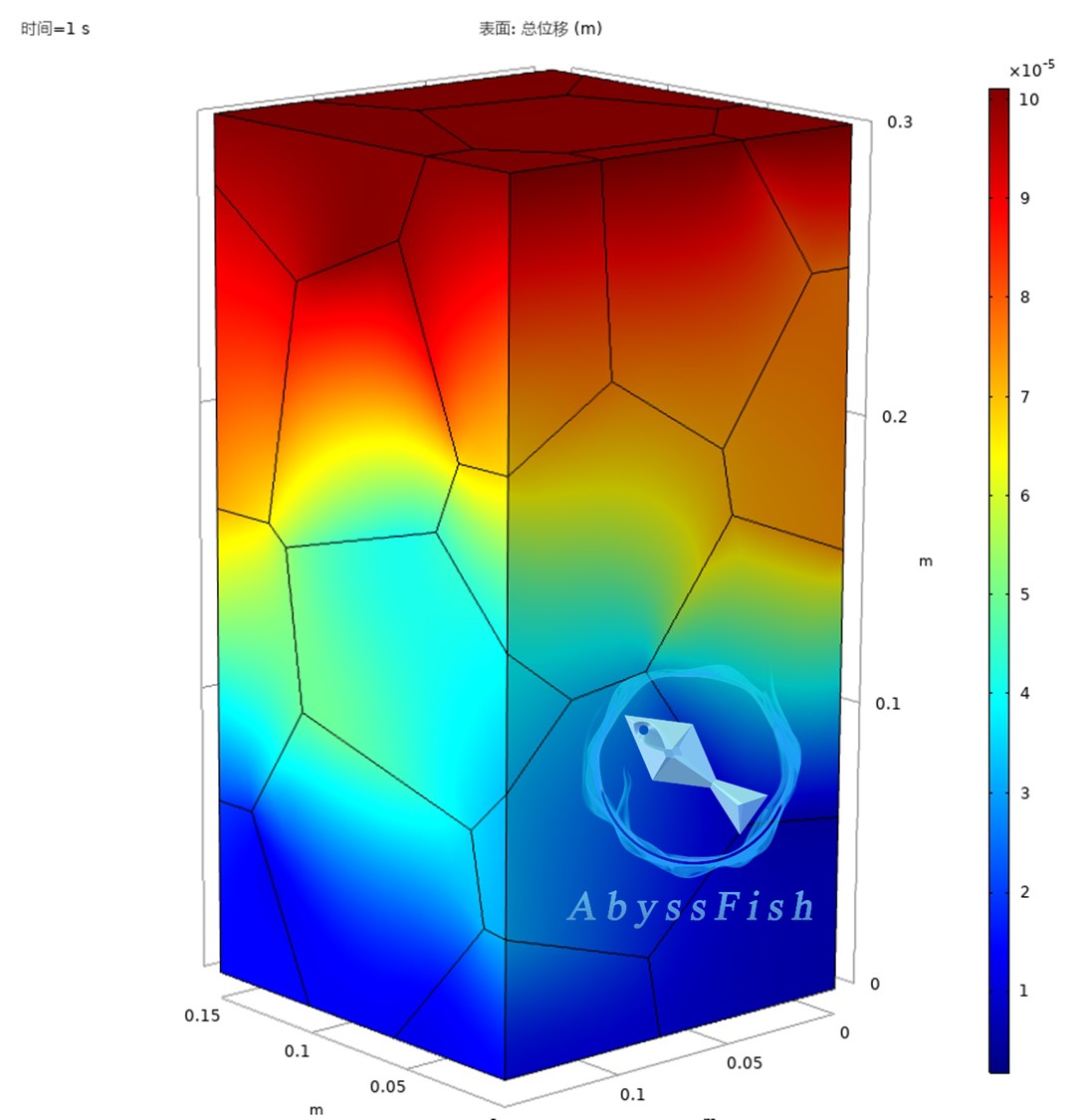
在Comsol中，我们可以通过“导入几何体”功能，选择合适的文件格式，将晶格顶点数据导入。然后利用Comsol的几何操作功能，比如“扫掠”“拉伸”等，将这些离散的点构建成具有一定厚度的三维晶体结构。

比如，如果我们导入的是二维Voronoi边界点，要构建三维晶体，可以沿着Z轴方向拉伸这些二维轮廓。在操作中，我们要注意设置合适的拉伸长度，以模拟真实晶体的厚度。

模型搭建好后，就该设置轴压模拟了。在Comsol的“固体力学”模块中，我们定义材料属性，比如弹性模量、泊松比等，这些参数要根据实际模拟的晶体材料来定。

接下来设置边界条件，对于轴压模拟，我们固定晶体的一端（比如底部平面），在另一端（顶部平面）施加均匀的轴向压力。这里可以在“边界条件”设置中，选择“固定约束”应用到晶体底部平面，选择“力”或“压力”边界条件应用到顶部平面，并设置合适的压力值。

在Comsol的方程视图中，我们可以看到固体力学模块的控制方程，以线性弹性为例，主要方程为：
σ_ij,j + f_i = 0  （平衡方程）
ε_ij = 1/2(u_i,j + u_j,i)  （几何方程）
σ_ij = C_ijklε_kl  （本构方程）

这里σij是应力张量，εij是应变张量，ui是位移分量，fi是体力，C_ijkl是弹性刚度张量。Comsol就是通过数值方法求解这些方程来模拟晶体在轴压下的力学响应。

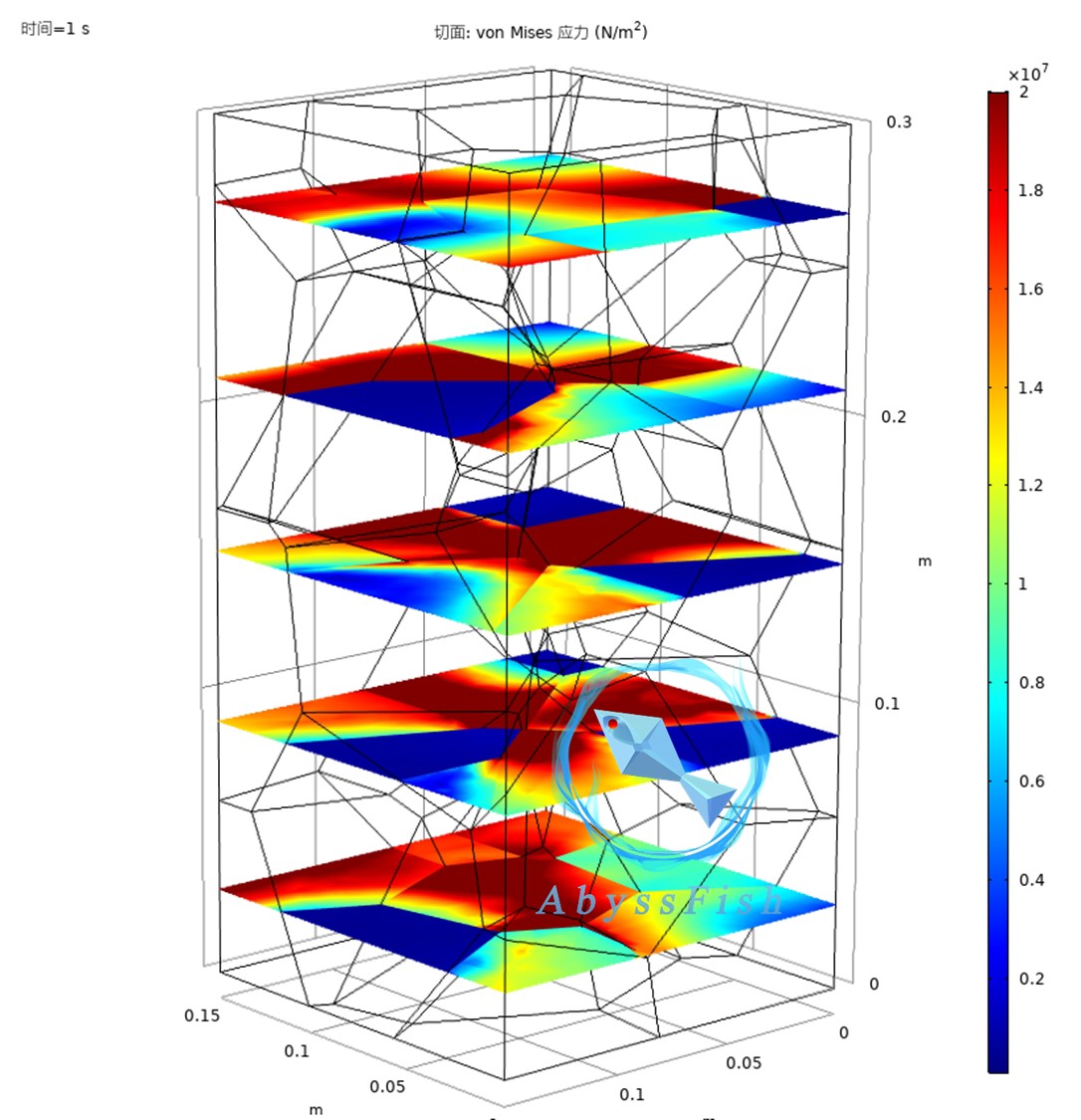
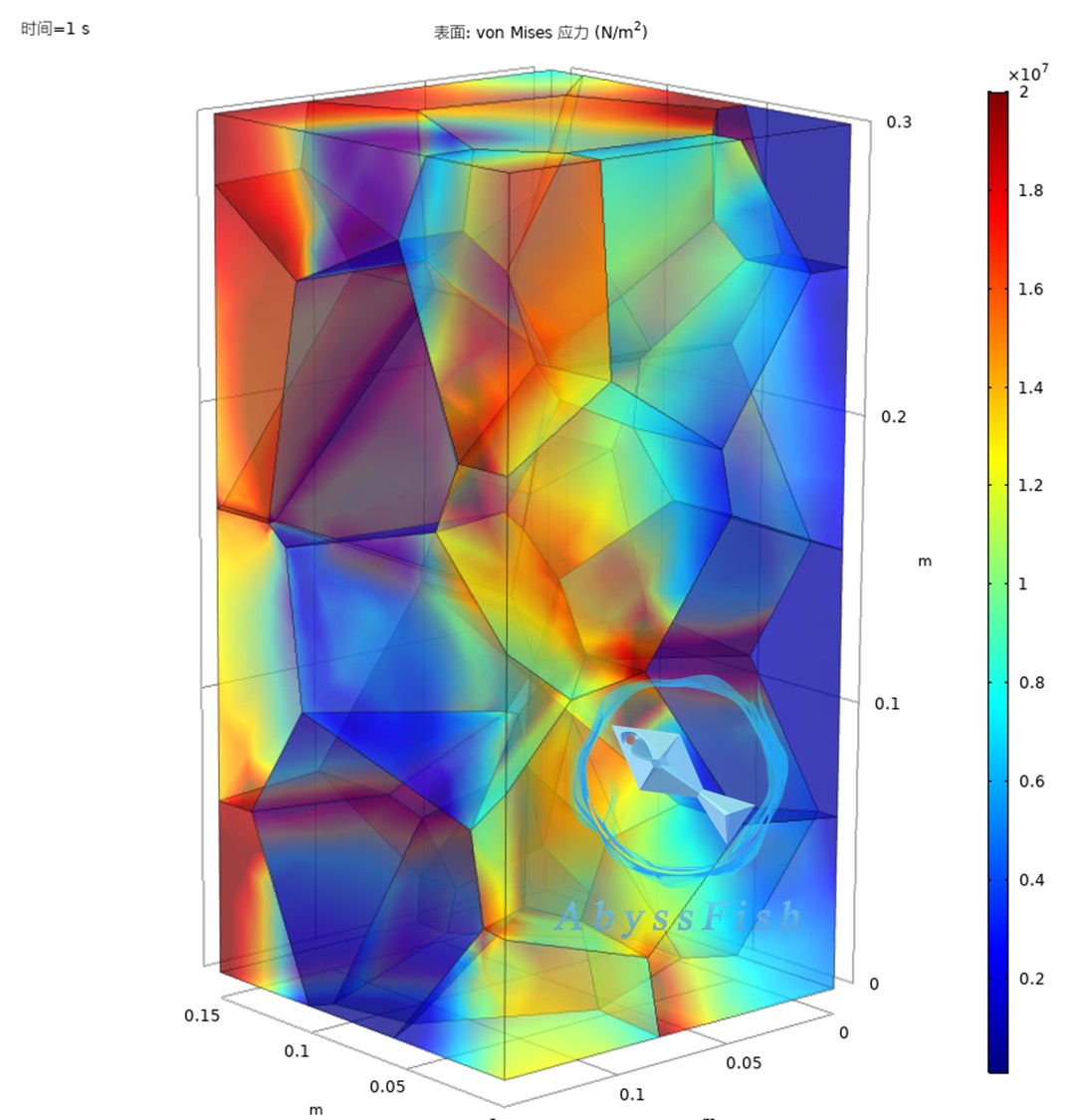
模拟完成后，我们可以查看各种结果，比如应力分布云图、应变分布云图等，通过这些结果来分析晶体在轴压下的力学行为，看看是否符合我们对该晶体材料的预期，是否存在应力集中等问题。

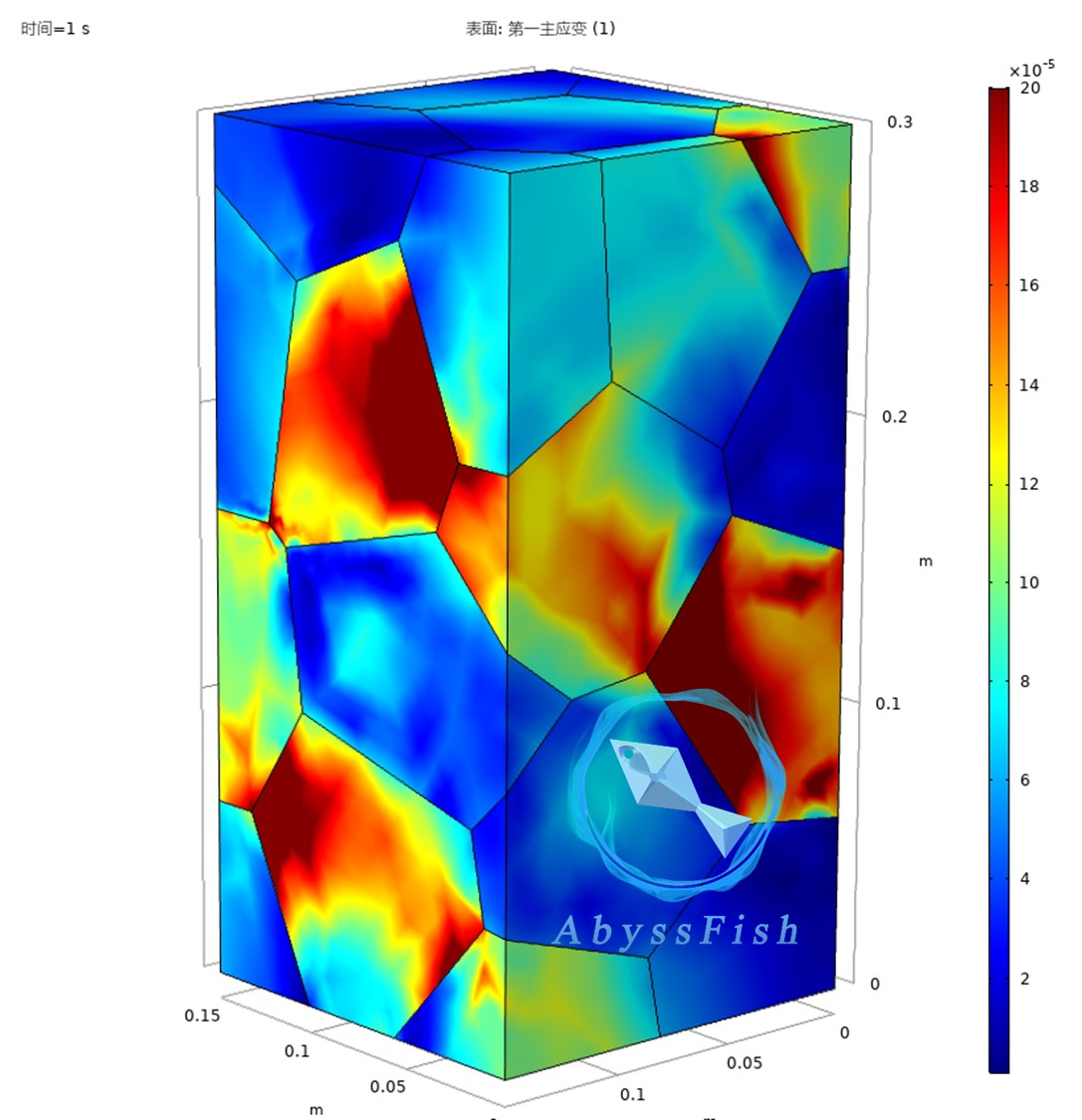
通过基于三维Voronoi算法的三维泰森多边形晶格分布构建Comsol三维晶体轴压模拟模型，我们能够更深入地了解晶体微观结构对其宏观力学性能的影响，为材料设计和优化提供有力的支持。