计量经济学模型研究：VAR模型、VECM模型及其脉冲响应与方差分解的实证分析

eviews stata计量经济学模型，VAR模型，VECM模型，脉冲响应，方差分解。

计量经济学里头的VAR模型，简直就是时间序列分析的万金油。这玩意儿全称叫向量自回归模型，说白了就是几个变量互相解释对方。比如研究GDP和通货膨胀率的关系，VAR能同时让这俩变量互为解释变量和被解释变量。Stata里搞个VAR模型，代码其实挺简单：

var gdp inflation, lags(1/2)
varstable
varlmar

第一行代码指定了用GDP和通货膨胀率建立VAR模型，滞后阶数选1到2阶。后面varstable检查模型稳定性，如果特征根都在单位圆内就稳了。varlmar做自相关检验，残差要是白噪声才算合格。但这里有个坑：选滞后阶数不能纯看软件默认，得用varsoc先做信息准则比较，不然可能过拟合。

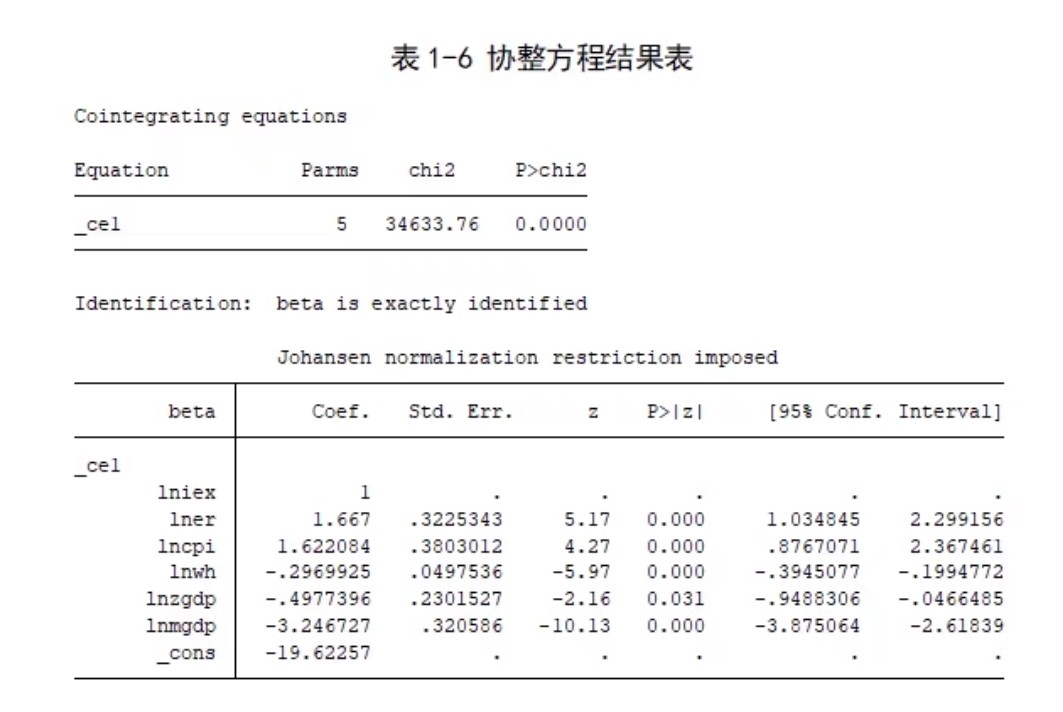
不过VAR有个致命问题——要求时间序列是平稳的。要是遇到非平稳数据，VECM（向量误差修正模型）就该出场了。比如两组存在协整关系的GDP数据，用EViews做VECM分三步走：

1. 先做协整检验

group gdp_group gdp1 gdp2
gdp_group.coint(none, lag=2)  # 无趋势项的协整检验

1. 确定协整秩（看迹统计量）
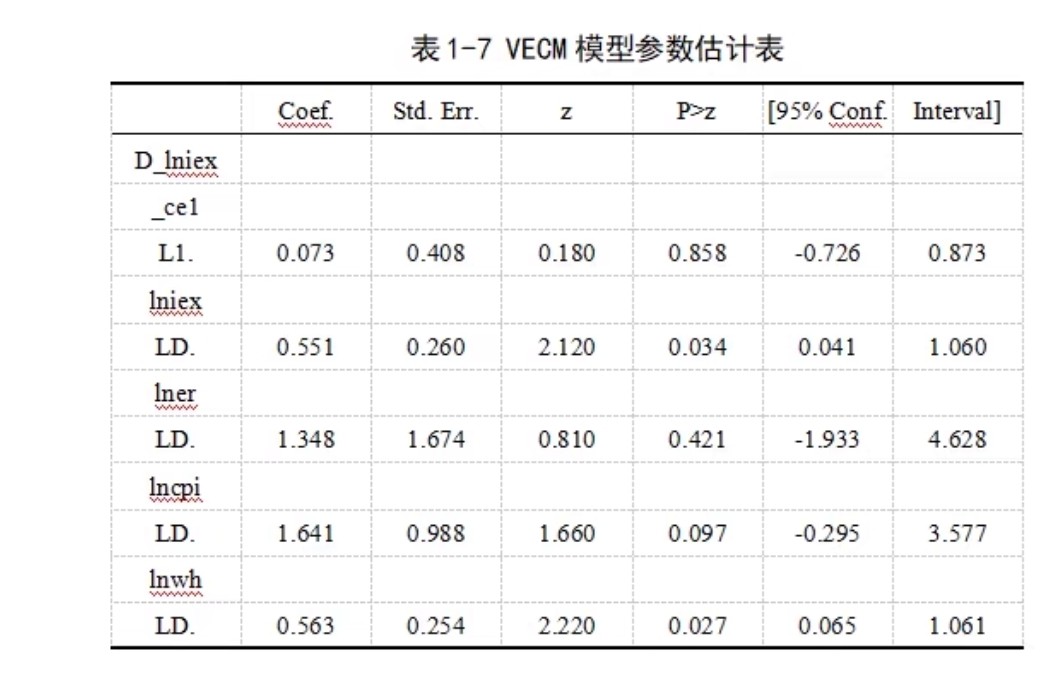
2. 建立VECM模型

vector_ecm.ls(cverr) d(gdp1) d(gdp2) @ gdp1(-1) gdp2(-1)

这里cverr参数特别关键，它控制了误差修正项的调整速度。有个冷知识：VECM结果里误差修正项的系数要是正数，可能暗示模型设定有问题，正常情况应该是负数才对。

说到实际应用，脉冲响应函数才是重头戏。比如央行加息对股市的影响，用Stata画脉冲响应图：

irf create var1, set(results) step(12)
irf graph irf, impulse(interest_rate) response(stock_index)

但要注意正交化脉冲响应对变量顺序敏感，把利率放前面和股票放前面结果可能完全相反。这时候就得用理论指导排序——通常外生性强的变量放前面。

方差分解更是个直观的工具，能看出不同冲击的重要性占比。EViews里操作完VAR后直接点View/Variance Decomposition就行，但要注意随着时间推移，分解结果会趋于稳定。曾经有个案例：原油价格波动中，30%来自自身冲击，60%来自美元指数冲击，这个结构三个月后就基本固定了。

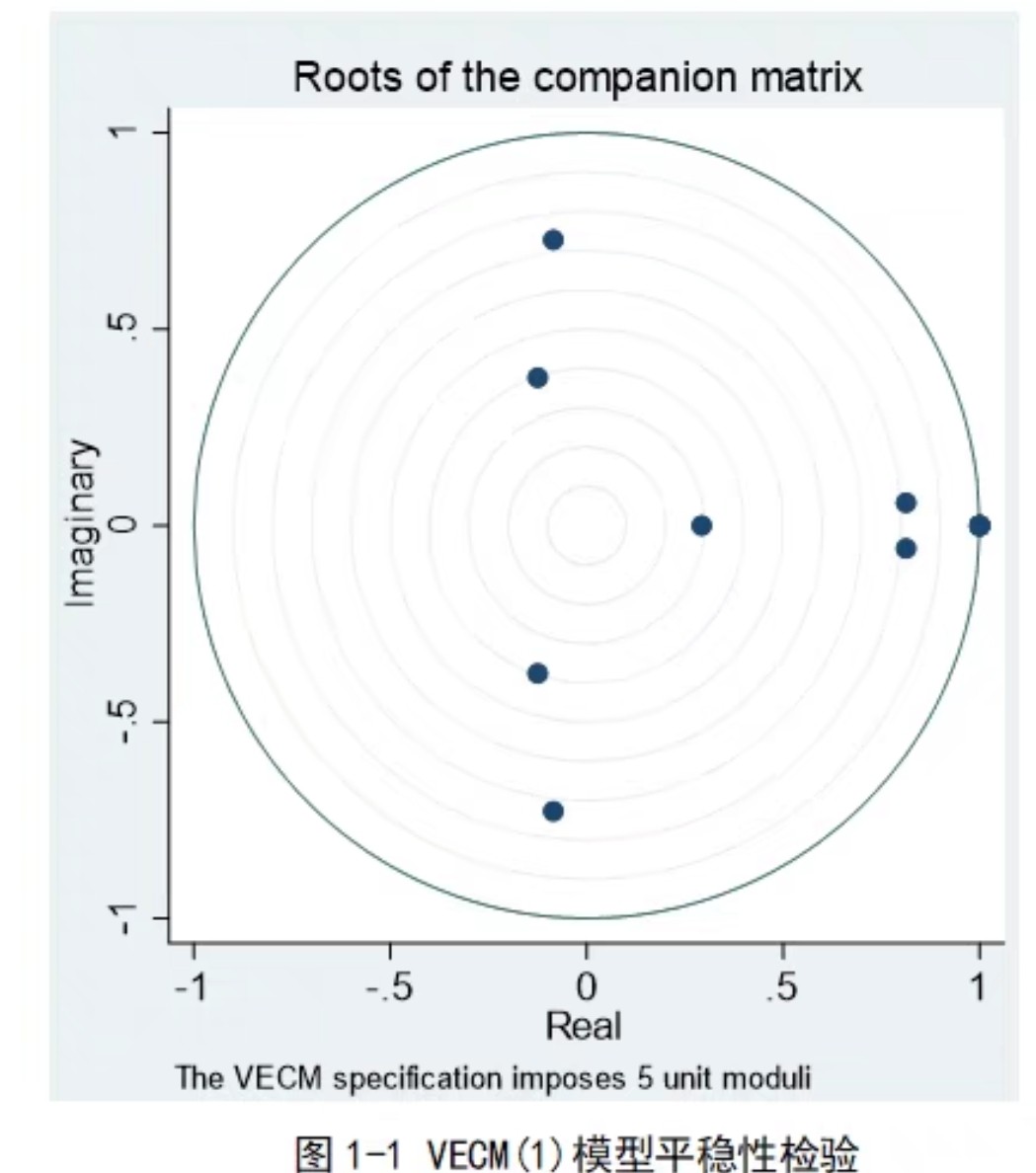
其实这些模型最怕样本量不足。有个经验法则：VAR模型最少需要样本量是变量数的10倍。之前见过用20个变量建模却只有100期数据的，结果脉冲响应曲线抖得像心电图，这模型基本就废了。时间序列分析嘛，有时候耐心等数据比急着跑模型更重要。