光伏MPPT仿真中的模糊控制策略优化与应用探讨

原创于 2025-11-10 19:15:00 发布 · 494 阅读

CC 4.0 BY-SA版权

文章标签：

光伏MPPT仿真-模糊控制

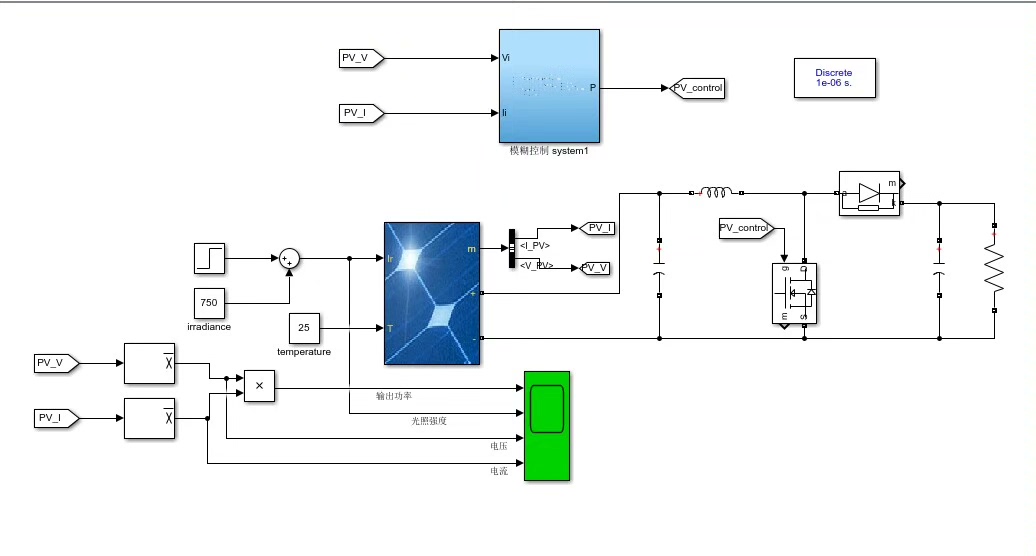
光伏系统里有个头疼的问题：太阳辐照度和温度一变，发电功率就跟着抽风。这时候就得靠MPPT（最大功率点跟踪）算法来揪住那个最高效率点，模糊控制在这事儿上特别有优势——它不需要精确数学模型，抗干扰能力还强，今天咱们就动手搭个简易版的仿真看看效果。

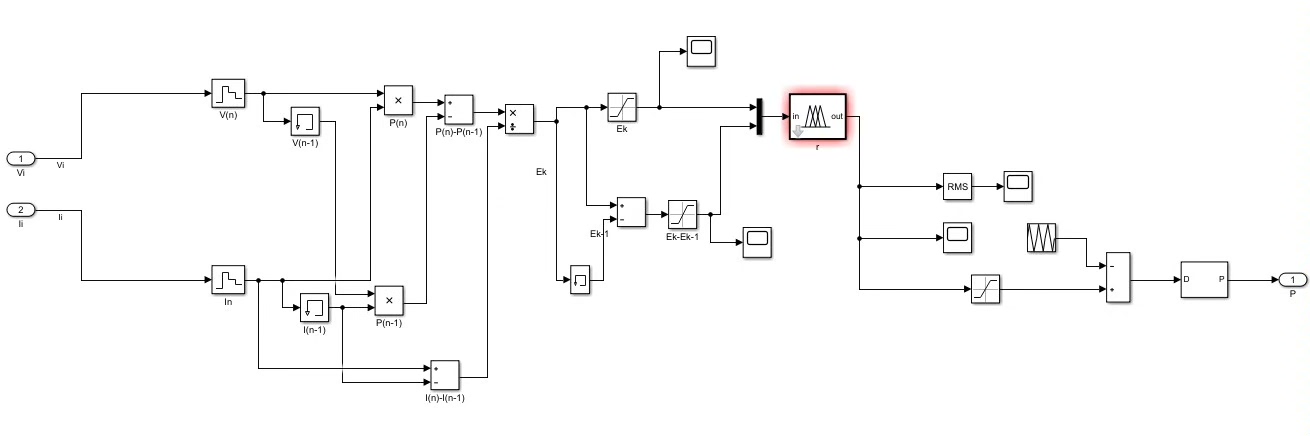
先理清楚模糊控制的核心思路。系统需要实时监测光伏阵列的输出电压和电流，算当前功率P和前一步功率Pprev的差值，再结合电压变化量来决定怎么调整工作点。这里用两个输入变量：功率变化E和电压变化率dE，输出是占空比调整量dutydelta。

上代码！用Python搞个模糊控制器类：

class FuzzyMPPTController:
    def __init__(self):
        self.e = [-0.5, 0, 0.5]  # 功率变化论域
        self.de = [-0.2, 0, 0.2] # 电压变化率论域
        self.output_range = [-0.05, 0, 0.05]
        
        self.mf = {
            'negative': lambda x, a: max(0, 1 - abs(x - a[0])/a[1]),
            'zero': lambda x, a: max(0, 1 - abs(x)/a),
            'positive': lambda x, a: max(0, 1 - abs(x - a[0])/a[1])
        }
        
    def compute_duty(self, E, dE):
        # 模糊规则库
        rules = [
            (E < 0 and dE < 0, 'positive'),
            (E < 0 and dE >=0, 'negative'),
            (E >=0 and dE <0, 'negative'),
            (E >=0 and dE >=0, 'positive')
        ]
        
        # 规则触发强度计算
        strength = []
        for condition, action in rules:
            if condition:
                e_val = self.mf['negative'](E, [-0.3, 0.2]) if E <0 else self.mf['positive'](E, [0.3, 0.2])
                de_val = self.mf['negative'](dE, [-0.1, 0.1]) if dE <0 else self.mf['positive'](dE, [0.1, 0.1])
                strength.append(min(e_val, de_val))
        
        # 加权平均去模糊化
        if sum(strength) == 0:
            return 0
        return sum(s * 0.05 for s in strength) / sum(strength)

这个类有几个关键点：隶属函数用了三角形和梯形组合，规则库用四组条件覆盖典型工况。注意compute_duty方法里的加权平均去模糊化——这里其实可以换成重心法，但简易版用线性加权反而更容易调试。

测试环节得模拟光伏阵列特性。用近似公式生成IV曲线：

def pv_curve(Irrad, Temp):
    V = np.linspace(0, 40, 100)
    I = Irrad * (8 - 0.05*(Temp-25)) - 0.5*V
    P = V * I
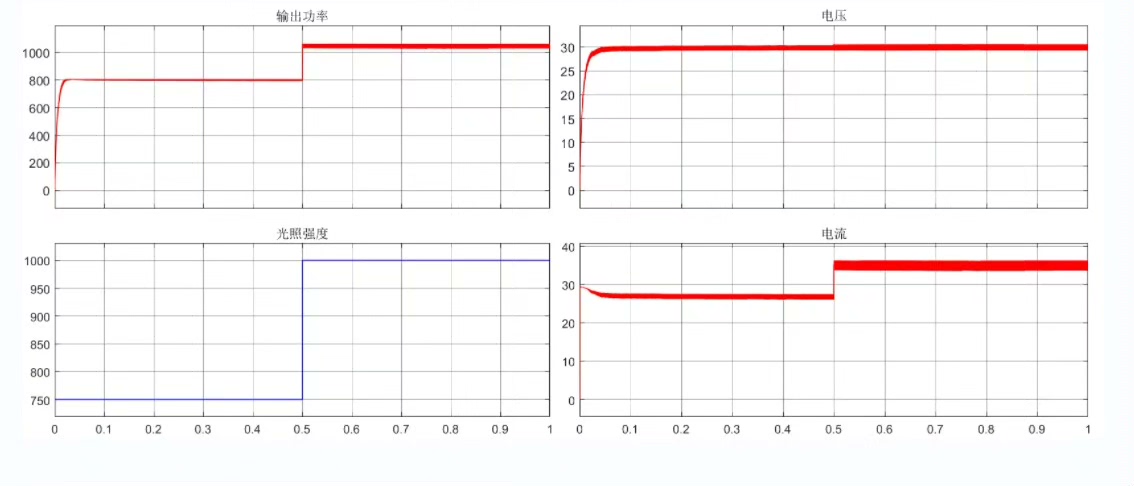
    return V[np.argmax(P)]  # 返回当前MPPT电压

当辐照度从1000W/m²突降到800时，对比下模糊控制和P&O算法的表现：

!仿真波形