基于MIMO阵列的动态液位检测

基于MIMO超声换能器阵列的动态液位精确检测

摘要

在许多情况下，由于液位动态变化，传统超声波液位检测会产生不可靠的估计结果。此外，某些情况下的液位变化不仅包括波动，还涉及液位的上升或下降。为了提高超声波方法在动态变化液位条件下液位测量的精度，本文提出了一种有吸引力的超声波方法，即基于多输入多输出超声换能器阵列的液位检测方法。该方法不同于早期的超声波液位检测方法，包括那些使用换能器阵列的方法。基于虚拟阵元技术，该方法采用多换能器阵列以降低系统复杂度和成本，并结合合成孔径技术实现液位的快速采样。此外，优化了每个扫描方向上合成孔径波束成形中聚焦位置的自适应搜索方案，以获得高精度的液位采样结果。所提出的方法通过仿真和真实系统进行了验证，并与传统单通道方法进行了比较。本文还提出了一种基于边界层理论和超声散射理论的液位超声回波信号仿真方法。仿真与实际测量结果表明，所提出的方法明显优于传统方法。同时，通过仿真研究了影响所提出方法的各种因素。研究表明，波束成形中的聚焦位置、回波信号信噪比以及液位波幅对所提出方法具有影响。然而，结果表明，只要在每个扫描方向上合理设置波束成形的聚焦位置，并有效控制回波信号噪声，所提出方法仍能保持良好的性能。

索引术语

声学，阵列，液位测量，误差，多输入多输出（MIMO）系统，换能器。

I. 引言

液位检测的精度是许多应用中的关键方面，例如石油、化工、气象工业等领域。现有的液位测量原理多种多样，包括机械、光学、电学、电磁和超声波方法。这些方法在液位测量方面已取得一定进展。机械法主要利用浮子漂浮在液面上来测量液位，通过滑动电阻、雷达或单个数码相机[1],[2]测量浮子的位置。机械法实现较为简单，但对液体种类有限制，且由于浮子姿态问题导致测量误差较大。光纤液位测量通过监测光纤的谷值波长偏移或光强度[3],[4]来实现。与其它传统方法相比，光纤具有高灵敏度、强抗电磁干扰能力、耐腐蚀性和体积小等优点[5]。然而，当前的光纤液位传感器普遍存在测量范围小和机械结构复杂等缺点。电磁式液位测量主要基于被测液体对电磁波的吸收或反射特性来确定液位高度[6]–[8]。不同介质对电磁波的吸收程度不同，利用该特性可实现不同介质的液位测量；此外，还可利用电磁波的反射特性测量飞行时间，进而计算液位。但电磁波衰减较大，测量距离较短，且成本较高。

电学方法主要包括电容法。传统的电容式液位传感器基于电容与液位之间的线性关系进行测量[9],[10]。该类传感器具有低成本、低功耗、良好的重复性和高线性度等优点。此外，通过添加参考电极板，该传感器可不受水质影响地检测水位，从而实时跟踪水位上涨情况[11],[12]。然而，在动态响应中仍存在滞后问题。此外，还需进一步研究其鲁棒性、寿命及环境条件的影响，以在湍流情况下实现更优的液位测量处理时间[11]。另外，结合高分辨率的300万像素CMOS相机以及在现场可编程门阵列（FPGA）中实现的硬件数字图像处理器，已在膜蒸馏应用中提出一种新型高精度自动液位测量系统[13]。该系统相比常规测量系统更为简单且成本更低。

超声波方法由于其更高的成本性能，已广泛应用于液位检测。经过发展，近年来我们可以看到这些显著的改进主要体现在一些领域，如发射信号优化、回波特征利用、飞行时间估计和接收信号处理。以下针对这些改进方面提供若干相应的示例。可通过分析并利用超声波的传播衰减和反射率来精确估计液位[14],[15]。超声兰姆波沿罐壁传播，可有效检测液位[16]。在飞行时间估计中，将无迹卡尔曼滤波器应用于接收信号，以估计回波包络并精确定位其起始点[17],[18]。此外，其他用于超声测距中的飞行时间估计策略完全可以应用于液位检测，并因超声波液位检测本质上属于一种距离感知技术而获得更高的估计精度[19]–[22]。在信号处理方面，首先使用自适应滤波器去除回波信号中的噪声和干扰，然后应用互相关方法识别飞行时间，从而实现精确的液位估计[23]。

然而，在实际应用中，液位的不规则变化可能导致上述液位检测方法性能不佳，因为有时液位是动态变化的，特别是那些不仅包含液面波动而且包含液位上升或下降的变化。因此，已开发出多种用于动态变化液位检测的方法。例如，在线支持向量回归算法被提出作为测量动态液位的一种解决方案。该方法不仅具有良好的性能，而且可以通过在线[24]更新预测模型。光学方法通过包含光强与液面晃动波之间关系的解析表达式以及波长和幅度的表达式，可以获得对应于静态和晃动液面的光模式。随后，可实现包括上升和衰减在内的晃动变化过程。该检测为无损且实时的[25]。

传统单通道超声方法也通过多次重复液位测量并对测量值取平均来检测变化的液位。然而，这种简单的方法仅限于液位波动但不涉及液位上升或下降的情况。此外，一种方法基于多个换能器。在此方案中，从液面以下某些位置沿预定方向发射具有不同载频的超声波，并由相应换能器接收回波，以确定整个液位上不同位置的液位值，然后通过对这些液位值取平均获得最终液位估计[26]。然而，该方法的复杂性和成本将随着液位采样数量的增加而上升。另一种方法采用支持向量机信号处理和分类方案实现精确液位确定[27]。由于其计算复杂，该方法在适应快速变化的液位时也存在困难。

我们之所以关注液位变化的精确测量，是为了在大雨情况下通过超声波实现精确雨量测量。在气象观测中实施雨量测量时，由于收集到的雨水不断注入测量容器，会导致液位动态变化。在此情况下，通过超声波实现理想的液位检测具有较大挑战性。因此，我们提出了一种超声波方法来实现这一目标。本文设计了线性超声换能器阵列，并在该方法中实现了对液位的扫描，从而实现液位的空间采样，并通过对液位样本取平均值得到精确的液位估计。为了以一种简单且低成本的超声波方式精确采样液位，我们借鉴了雷达研究中的最新相关成果，提出了一种基于多输入多输出（MIMO）超声换能器阵列的独特液位测量方法。

所提出的方法仍由若干组成部分构成：换能器阵列、信号发射与接收通道以及信号处理单元。基于MIMO换能器阵列的动态液位超声波测量结构如图1所示。然而，该方法在本质上不同于传统相控阵方法。换能器阵列被设计为形成虚拟相位阵列结构，从而利用虚拟阵元技术显著降低系统的复杂性和成本。在信号处理方面，可采用合成孔径技术实现液位上任意位置的快速采样。此外，优化了每个采样方向上的聚焦位置自适应搜索，以获得高精度的液位样本。同时，优化了线性调频连续波（FMCW）脉冲作为发射信号。

II. 提出的方法及其关键方面

A. 换能器阵列结构

根据MIMO相控阵雷达方案[28]，M个发射换能器和N个接收换能器

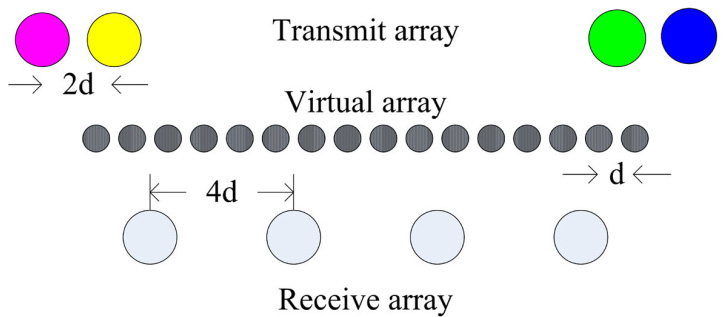
所提出方法的传感器被布置成线性阵列。具体而言，接收换能器位于阵列中部，发射换能器分为两组对称分布在接收换能器两侧。假设M= 4和N= 4，换能器按照一定规则排列成线性阵列，从而合成一个包含16个虚拟换能器的均匀线性阵列。这意味着通过合理布置发射和接收换能器的位置，可以生成期望的虚拟相控阵阵型[29]。图2展示了构成线性MIMO阵列的超声换能器布置示意图。从图2可以看出，这是一种对称阵列结构。为了确定所有实际换能器和虚拟换能器的位置，需要建立一个坐标系，其中阵列中心为坐标原点，换能器的中心线与坐标系的x轴重合。若要求构建一个非重叠、等间距为d的均匀线性虚拟阵列，则相干MIMO换能器阵列的实际换能器应按照以下设计规则进行布置：发射换能器间距为dt= 2d，接收换能器间距为dr= Md，每组由M/2个换能器组成的发射组与接收阵列边缘换能器之间的间隙为dtr= d。所设计的MIMO换能器阵列的物理长度为(MN+ M − 2)d，虚拟阵列的长度为(MN−1)d。需要注意的是，此处不考虑换能器之间的耦合效应。

考虑到实际系统中采用的圆形换能器直径为12毫米，我们将d设为15毫米。因此，线性换能器阵列的物理长度约为282毫米，虚拟阵列的长度约为225毫米。如果发射换能器的波束角为 20◦，当阵列与液面之间的距离为 1000毫米时，沿x‐坐标轴方向的超声辐照范围约为868毫米。此外，由于形成的虚拟阵列间距大于传统相控阵所要求的0.5 λ距离，因此无需考虑栅瓣的出现。根据上述方案，从发射阵列到接收阵列共有M × N个不同的传播通道。如果接收阵列能够识别接收信号的发射源，则仅使用M+N个实际元件即可获得由M ×N个元件组成的虚拟相控阵[30]。与传统相控阵相比，可节省(M × N) −(M+ N)个元件或传播通道。这种虚拟阵元技术实际上有助于实现降低系统复杂度和成本的目的。

B. 调频连续波信号模型

相干MIMO检测系统的多样性可通过采用时分复用、频分复用、空间编码和正交信号[31]来实现。本文选择调频连续波脉冲作为发射信号，因为调频连续波技术能够实现低成本和紧凑型系统设计，并支持较低的采样率。此外，调频连续波脉冲信号具有大时宽带宽积，可提高距离分辨率。这些调频连续波技术的优势有助于降低系统的复杂性和成本。此外，调频连续波技术已成功应用于稀疏相干MIMO雷达[28],[29],[31]–[34]，相关技术可为本文提出的方法提供参考。

发射换能器的调频连续波脉冲信号由以下形式给出:

$$ s_t = \exp{j(2\pi f_c t + \pi K t^2)}, |t| \leq T_c/2 $$ (1)

其中，$T_c$为脉冲持续时间，$f_c$为载波频率，$K$为调频斜率，由发射信号的带宽B和脉冲持续时间$T_c$定义，即$K= \pm B/T_c$。正的K表示升调频，负的K表示降调频。通常，发射的调频连续波脉冲的持续时间不重叠，即脉冲重复频率(PRF) ≤ 1/$T_c$。然而，我们根据指定的最大探测距离$R_{max}$或超声波到达最大探测距离并返回接收换能器所需的最长时间$T_{max}$来确定PRF，即PRF ≤1/$T_{max}$=$c/2R_{max}$。其中，$c$表示声速。

接收信号可以被建模为

$$ s_r(m, n, t)= \int_{R_{max}} \alpha(p)A_r(p; m, n, t)s_t(t - \Delta t_{m,n}) dp $$ (2)

其中，$m,n \in N$分别为发射和接收阵列的换能器索引，$\alpha$为反射率函数，$p \in R_{max}$为照射区域中的点目标，$A_r$为声波的幅度函数，$\Delta t_{m,n}$为调频连续波脉冲信号从第m个发射换能器$x_m$到点目标$p$再返回到第n个接收换能器$x_n$的时间延迟

$$ \Delta t_{m,n}= d_{p;m, n}/c=(|p −x_m| + |p −x_n| )/c $$ (3)

其中强调提出的方法仅限于近场条件，而非远场条件[29],[35]。由于相对于轴线不存在常数近似角度$\theta$，因此从每个虚拟阵元$x_{m,n}$到点目标$p$的声波传播距离不能简单地表示为$d_{p;m,n}= 2R_p+ 2x_{m,n} \sin \theta$[28]，特别是当点目标$p$非常靠近换能器阵列时，其中$R_p$是点目标到换能器阵列的距离。

在对接收信号应用去斜率技术和低通滤波后，得到的信号被建模为

$$ s(m, n, t)= \int_{R_{max}} \alpha(p)A_r(p; m, n, t)\exp{j 2\pi\phi(p; m, n, t)}dp. $$ (4)

然后，相位函数的偏导数可以提供如下：

$$ \frac{\partial\phi}{\partial t}= K\Delta t_{m,n}. $$ (5)

由于某个信号的相位函数的偏导数对应于其频率成分，因此可以得到虚拟传感器$x_{m,n}$接收到的信号的频率表达式，即$f_{m,n}= K\Delta t_{m,n}$，其中包含目标的距离信息。因此，声波从发射换能器$x_m$传播到目标再返回接收换能器$x_n$的距离，或虚拟单元$x_{m,n}$与目标之间的距离可通过以下方式计算

$$ d_{p;m, n}= cf_{m, n} /K= c\Delta t_{m, n}. $$ (6)

从(5)和(6)可以看出，去斜率处理后的相位函数包含了距离和方位信息。这也意味着，在对接收信号进行去斜处理并将时间延迟转换到频域后，我们能够有效确定目标的距离。此外，从(7)中我们仍然可以观察到，$f_{m,n}$和$d_{p;m,n}$随着时间延迟$\Delta t_{m,n}$的变化而不同。因此，通过调节时间延迟可以改变接收信号的相位。这是基于MIMO的调频连续波成像技术中时域波束成形的基础。

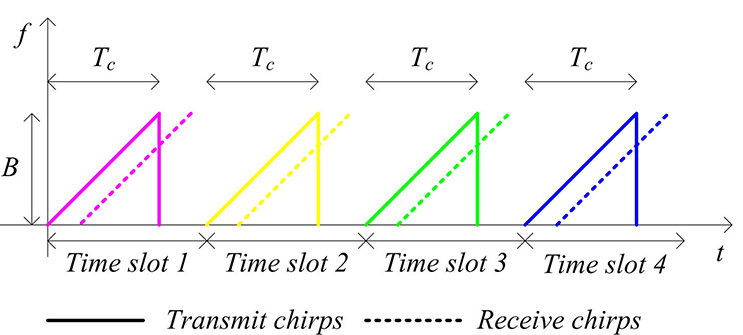
为了在合成M ×N MIMO信道时区分发射通道，通常采用时分方案在不同的时隙将发射通道开启或关闭以进行辐射。通过时分传输，发射换能器依次被激活，而所有接收换能器同步接收回波信号。对所有时隙的发射信号接收构成一轮扫描，共获得M ×N个信道的信号。本文仍然采用这种简单但可靠的信号传输方案。结合第二节II‐A中的四个发射和四个接收换能器，该信号传输方案由图3中的时频图描述。在实施该方案时，时隙根据最大探测范围确定，并且线性调频持续时间的边界需满足条件$T_M< \lambda/(4(M − 1)v)$且小于时隙，其中$T_M$为最大持续时间，$v$为目标速度。同时，还需综合考虑分辨率、回波功率、目标的加速度和速度等因素。

C. 数字波束成形算法

许多数字波束成形（DBF）方法已经存在[28],[29],[36]–[40]。本文中，我们仍然考虑

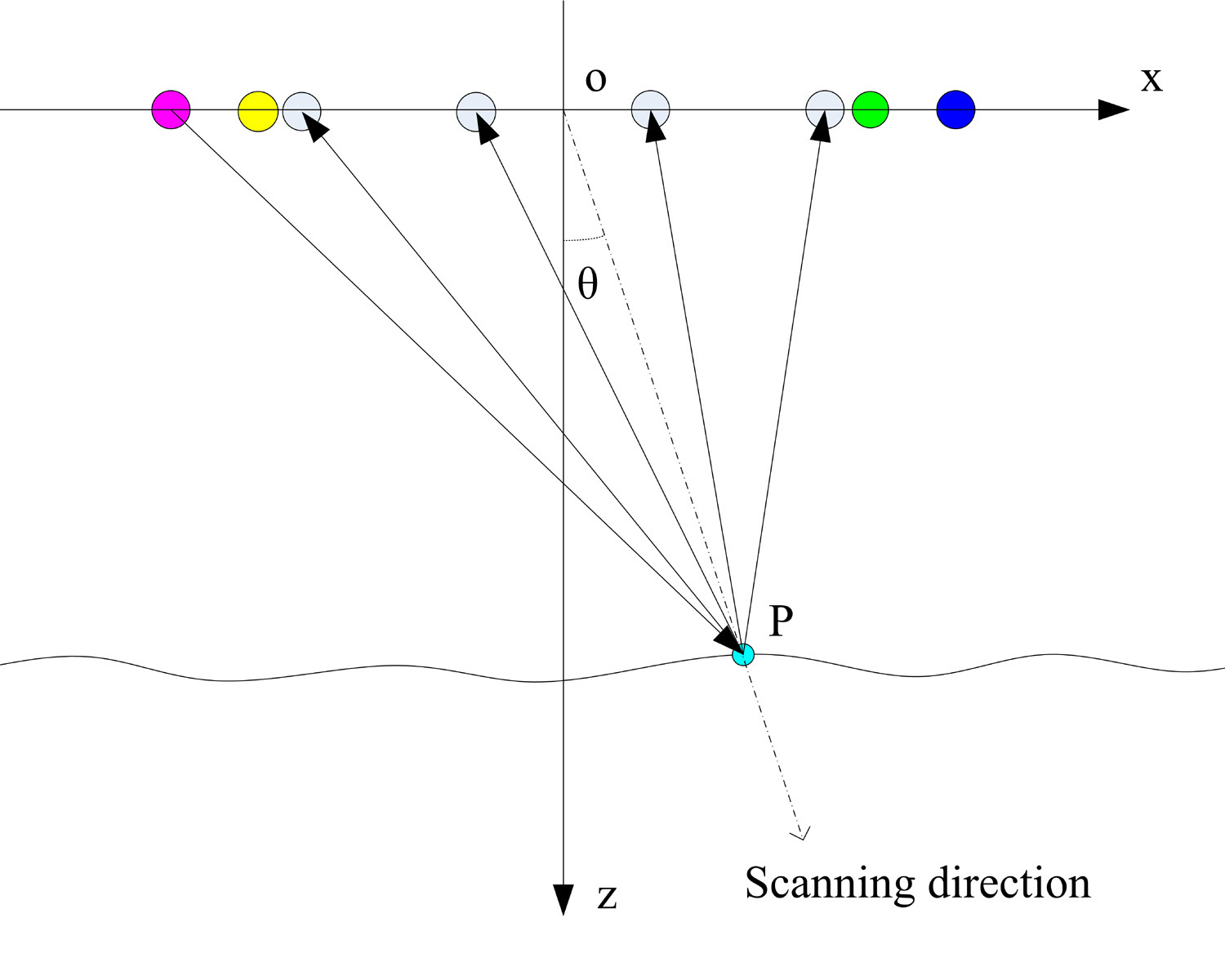
传统的时域DBF算法。基于上述对称的阵列结构，我们在实施数字波束形成之前，首先建立一个坐标系，以便于计算每个虚拟换能器的时间延迟。由于我们主要考虑二维横截面扫描，因此设置了一个二维坐标系来确定所有阵列换能器的相应位置，如图4所示。在该坐标系中，x轴与换能器阵列的中心线重合，换能器关于z轴对称，而z轴为超声波传播方向。在图4中，假设点P是液位上的一个期望的空间采样点，将其视为点目标，因此它也是波束成形中的聚焦位置。假设已知点P的坐标，则从坐标系原点指向点P的方向被视为合成超声波束的方向或扫描方向。此外，合成波束的轴向方向与z轴之间的夹角$\theta$被视为方位角。

根据阵列中所有换能器的坐标以及点目标的位置，可依据(3)式求得每个虚拟换能器的时间延迟。然而，这些时间延迟需用不同的相对时间延迟$\tau_{m,n}$进行补偿，即$\Delta t_c= \Delta t_{m,n}+ \tau_{m,n}$，其中$\tau_{m,n}$表示波传播从参考点到虚拟阵列中各个换能器的时间差。$\Delta t_c$由于对$\tau_{m,n}$的补偿而成为一个常数。因此，波束成形后的信号可表示如下：

$$ s_r(t)=\sum_{m,n} \int_{R_{max}} \alpha(p)A_r(p; m, n, t)s_t(t −\Delta t_c) dp . $$ (7)

由于回波信号在接收过程中被采样，我们可以数值实现延时求和和去斜。经过低通滤波后，可获得频率下变频信号以估计目标距离。因此，可通过以下方式计算换能器阵列中心与点P之间的距离

$$ d_{o,p}= c\Delta t_c/2. $$ (8)

D. 动态液位检测

在接收所有回波信号后，将总共四个接收通道的数据重组为16个回波信号通道，每个通道对应一个虚拟相控阵换能器。在此基础上，我们进行相关的信号处理并估计液位。综上所述，动态液位检测的实现主要包括以下几个步骤。首先，在某一预设扫描方向上确定数字波束形成（DBF）或合成波束的聚焦位置。从图4可以看出，液位上空间采样点P的位置是随机变化的，而DBF的聚焦位置与采样点P重合的概率较小。因此，聚焦位置偏离采样点P是导致采样误差的主要原因之一，这一点将在下文的仿真部分中得到验证。为此，正确确定聚焦位置十分必要。我们的考虑是：在执行DBF之前，首先利用对应于虚拟换能器 $x_{2,1}$或$x_{3,4}$的接收信号$s_r(2,1, t)$或$s_r(3,4, t)$获得一个粗略液位值，然后根据该粗略液位估计确定一个聚焦位置范围。

其次，在预设扫描方向上确定聚焦位置和液位的采样值。在聚焦范围内沿预设方向的一些点被假设为潜在聚焦点。对每个潜在聚焦点实施数字波束形成和脉冲压缩处理。当压缩信号的主瓣幅度达到最大值时，该潜在聚焦点对应的位置即为期望的聚焦位置，并可通过聚焦位置到阵列中心的距离和方位角$\theta$得到该方向上的采样值。需要改变扫描方向并重复此过程，直到获得各个预设方向上的聚焦位置和采样值。最后，通过对所有方向的采样值取平均，实现液位精确测量。所提出方法用于估计变化液位的完整实现过程可由图5所示的框图明确描述。

III. 基于仿真信号的验证

本节将通过仿真验证我们方法的可行性。同时，将所提出的方法与传统信号通道检测进行比较。此外，我们还考察了某些相关因素对方法的影响，例如波束成形中的聚焦位置、回波信号信噪比以及波动液位的波幅。通过对相关仿真结果的分析，旨在进一步改进提出的方法。

A. 回波信号仿真

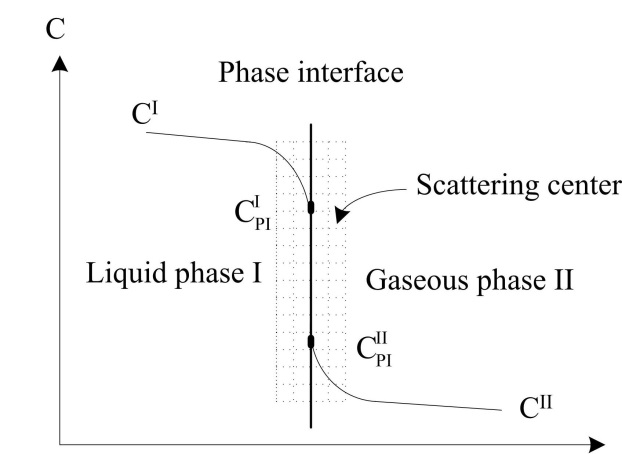
液位回波信号的仿真是一个非常困难的工作，因为液位的气‐水界面是非常复杂。基于边界层理论[41]，水分子和空气分子在向相界面扩散时必然会遇到阻力。因此，在气‐水界面附近会形成水分子浓度差。界面浓度的变化如图6所示。在模拟液位回波信号时，为了简化，我们在相界面两侧设置了一些细小的网格，每个网格被视为一个独立的点目标散射中心，并根据水分子浓度设定每个散射中心的散射强度，如图6所示。当超声波照射到液位时，回波信号是辐射区内各个散射中心返回信号的求和。根据超声散射理论[42]，这种方法适用于较大的检测目标。接下来的主要工作是建立来自单个点目标的信号模型。

存在几种超声回波信号的仿真方法[19],[27],[43]。其中一种模型仅涉及若干基本因素，被广泛应用于超声成像和检测研究[27],[43]。由于该模型能够表征多种目标类型和位置下的观测信号，我们参考该模型，并通过将单正弦信号替换为调频连续波脉冲信号对其进行改进。因此，来自点目标的发射调频连续波脉冲的回波信号可近似表示为

$$ s_r= a_0(t −\Delta t)^2\exp[−a_1(t −\Delta t)]u(t −\Delta t) × \exp{j(2\pi f_c+ \pi K(t −\Delta t)^2 )}+ w(t). $$ (9)

该模型仅为一个调频连续波脉冲，其包络由一个抛物线函数与指数衰减函数的乘积构成。其中，$a_0$和$a_1$分别为信号的形状参数和幅度参数，$u(t −\Delta t)$是延迟了$\Delta t$的单位阶跃函数，时间延迟$\Delta t$对应超声波从发射换能器到目标再返回接收换能器所需的时间，$w(t)$是均值为零、方差为$\sigma^2_\mu$的高斯白噪声，该噪声可能包括热噪声、声学噪声、幅度量化误差等。

考虑到超声波束类似于手电筒光束，其横截面为圆形图案，波的强度在中心最强。因此，随着半径的增加，声压必须降低

表I 仿真参数
参数
载波频率 $f_c$
带宽 $B$
脉冲持续时间 $T_c$
声速 $c$
换能器间距 $d$

表II 点目标与阵列单元的坐标系
换能器
$x_1$
$x_2$
$x_3$
$x_4$
$x_5$
$x_6$
$x_7$
$x_8$

基于能量守恒的波束横截面。此外，我们考虑使用一对相同的换能器的配置，其中一个换能器作为发射器，另一个作为接收器。根据互易原理，来自超声波辐射区内点目标的回波信号幅度由以下[43],[44]:加权

$$ W(r_1, r_2, \theta_1, \theta_2) = \sim \varepsilon A_0 r^{3/2}_0 r_1 r^{1/2}_2 r^{-(\theta^2_1+ \theta^2_2)/2\sigma^2_T} $$ (10)

其中，$r_1,r_2> r_0$, $r_1$和$r_2$分别为目标与发射传感器和接收换能器之间的距离，$\theta_1$和$\theta_2$分别为发射波中心和来自目标的反射波的角偏差，$\sigma_T$为波束宽度参数。为简化起见，$r_0 = \sim 10$厘米且$A_0= 1$。

根据单个目标的信号模型，我们在单通道检测系统中对静态液位的回波信号进行仿真，并根据实际超声波液位测量情况设置表I所示的相关参数。此外，所有换能器的坐标由表II确定。换能器阵列到液位的距离假设为600毫米，即到相界面的距离。辐射区为半径200毫米的圆形扇区，由两层不同水分子浓度的水‐气膜和一层水组成。每一层被划分为若干网格，每个网格代表一个孤立点目标的散射中心。每个网格的尺寸为2毫米 × 2毫米。此外，我们使用方差来描述同一层内各个散射中心散射强度的微小差异。

液位上辐射区的相关参数设置如下：水中散射中心的散射强度

基于MIMO超声换能器阵列的动态液位精确检测

（液相）、水‐气膜I、水‐气膜II和空气（气相）的反射系数分别为0.95、0.70、0.35和0.05，其方差统一为 0.0025。实测与仿真回波信号来自液位的情况如图7所示。

经过基于快速傅里叶变换（FFT）的脉冲压缩处理后，两个信号的压缩信号如图8所示。根据图7和图8可知，两种信号的波形相似，且其压缩信号的主瓣和旁瓣特征也非常相似。这表明我们提出的液位回波信号仿真方法是可行的，仿真信号可用于验证所提出的方法。

此外，我们还根据上述换能器阵列对静态液位的16个通道回波信号进行了仿真；图9中所示的对应于虚拟换能器 $x_{1,1}$, $x_{1,4}$, $x_{2,3}$, 和 $x_{3,4}$ 的信号也用于验证该信号仿真方法对所构建的换能器阵列同样有效。从图9可以明显看出，由于散射中心与换能器之间的相对位置不同，回波信号中的调频连续波脉冲在幅度和回波时间上均存在差异。对于信号幅度的差异，主要原因是当不同的发射换能器进行照射时，散射中心位于波束横截面上的不同位置。随后，所有16个通道信号执行了

数字波束形成和合成信号执行脉冲压缩。在对所有信号实施时间延迟和求和时，将聚焦位置设置在相界面与波束扫描方向的交点处。该压缩信号与未进行时间延迟的直接求和信号的压缩信号进行比较，如图10所示。可以看出，经过时间延迟的压缩信号具有很高的主峰与旁瓣比，主瓣具有窄宽度，并精确对应于液位相界面的距离。图10的结果证明了传统的时域数字波束形成是可行的，并且能够获得预期的结果。

最后，我们对波动液位的回波信号进行了仿真。为了获得从波动液位反射的回波信号，首先生成一条波形曲线以模拟波动液位的气‐水相界面。该曲线两侧分别具有散射强度不同的水‐气膜。采用与前述静态液位完全相同的方法，回波信号精确地来自波动液位上各散射中心的反射。为了简化起见，我们生成一条近似的正弦波曲线来表示相‐空气

变化液位的界面，参数设置如下：波形周期为2，波形幅值为20毫米，超声辐射区长度为800毫米，当液位平静时液位距离为1000毫米。此处需注意，液位距离是指传感器阵列与液位之间的范围。当采集16通道数据后，通过实施相应的信号处理可获得液位样本。

B. 估计结果

首先，我们根据图5中描述的实施流程对静态液位进行仿真估计。在仿真中，换能器阵列到液位的距离设置为 1000毫米，回波信号信噪比为10。此外，将估计结果与传统单通道检测方法的结果进行了比较。为了简化处理，将虚拟换能器 $x_{2,1}$ 或 $x_{3,4}$ 对应的信号视为传统方法的接收信号。同时，在使用传统方法时考虑了发射和接收换能器的布置，以减小估计误差。根据实施流程，通过 $x_{2,1}$ 或 $x_{3,4}$ 的信号获得粗略液位值，为1000.31毫米。因此，由于是静态液位情况，聚焦位置范围确定为1000.31 ± 10毫米。在确定的聚焦位置范围内，沿扫描方向采用每步2毫米的步长来确定潜在的聚焦位置。所提方法和传统方法的估计结果分别为999.77毫米和1000.31毫米，相应的绝对误差仅为 0.23毫米和0.31毫米。该仿真表明，在静态液位情况下，两种方法没有明显差异。

其次，我们继续对波动液位估计进行仿真。同样，将传统方法与本文提出的方法进行了比较。传统方法的测量结果为1005.23 mm，由于该结果是通过 $x_{2,1}$ 或 $x_{3,4}$ 的信号计算得到的，因此也作为粗略的液位估计。考虑到波幅为 20 mm，聚焦位置范围设定为993.61 ± 40 mm。此外，在变化液位测量中，根据横向分辨率和空间采样理论[28],[45]确定了采样密度或单位长度内的采样点数。此处直接指定每100 mm长度上的单位长度采样点数为10，整个被测液位范围内共包含80个采样点。采用相同的方法求解每个扫描方向上的聚焦位置，即可获得不同方向上液位的采样点。最终液位估计为999.8 mm，液位样本的最大误差和方差分别为0.2598和0.7477 mm。相关结果，包括液位样本估计及其对应的估计误差，如图11所示，进一步验证了提出的方法的可行性。从图11可以看出，由液位样本估计形成的曲线几乎与假设液位的水‐气界面重合。此外，

液位样本估计误差呈不规则变化，且样本的误差非常小。该仿真还表明，焦点位置搜索方法是有效的，并减小了对液位样本的影响。因此，仿真结果与以下事实一致：在变化的液位条件下，我们的方法能够实现高可靠性估计。

C. 影响因素验证

本文中，我们仍考察了若干影响所提方法的相关因素，包括噪声、聚焦位置、液位波幅等。对于噪声影响的考察，我们主要考虑上述静态液位情况。因此，在回波信号仿真中通过调节空气散射强度来改变接收信号的信噪比。由于每个传感器位于不同位置，各虚拟换能器接收到的信号信噪比可能不相等。与之前相同，对应于虚拟换能器 $x_{2,1}$ 或 $x_{3,4}$ 的仿真信号作为传统方法的接收信号。这样做的另一个优点是，两种方法基本保持相同的噪声水平。在本项验证中，回波信号信噪比从−20变化到25 dB。

与噪声影响相关的检测结果如图12所示。从图12可以看出，在16至25分贝的高信噪比下，两种方法没有明显差异，两种方法的最大误差均不超过0.65毫米。然而，在0至 16分贝的中等信噪比下，提出的方法明显优于传统方法。随着回波信号信噪比进一步降低，传统方法变得完全失效。然而，即使回波信号信噪比从 −10降至0分贝，我们的方法仍能保持低于1.85毫米的较小测量误差。实验结果表明，我们的方法在抗噪声性能方面优于传统方法。该检测对我们非常重要，因为提出的方法在雨量测量中的应用是

总是伴随着由高空气湿度引起的噪声干扰，尤其是在接近液位的区域。需要指出的是，我们的方法具有良好的抗噪声性能，这得益于波束成形后合成信号的信噪比提升。

为了检验焦距位置对提出的方法的影响，我们仍然使用上述静态液位的仿真数据。在本验证中，主要考虑合成超声波束对液位进行采样时，焦距位置沿扫描方向的变化。为简化起见，仅考虑扫描方向与换能器阵列的z轴重合的情况。采样误差与焦距位置变化之间的关系如图13所示。同时，本节中也改变了接收信号信噪比。

基于图13可以明显看出，当聚焦位置向水‐气界面移动时，误差最小且压缩信号的幅度最高。然而，这表明在靠近水‐气界面的小范围内，测量精度不受聚焦位置的影响。

水‐气界面。例如，当聚焦位置位于约 1000 ± 5 mm范围内时，误差较小，达到0.16 mm。此外，该范围在降低接收信号信噪比时仍能保持测量精度不受影响。另一方面，本文还验证了上述建立的聚焦位置搜索规则是合理的。此外，该规则将确保数字波束形成中聚焦位置自适应地跟踪液位变化，从而实现最优的测量结果。

最后，我们仍然评估了液位波幅对提出的方法的影响。为此，我们对具有不同波浪尺寸的波动液位进行了仿真测量。这里需要说明的是，波浪尺寸指的是波的最大峰值。为简化起见，在仿真中设定了六种波浪尺寸，分别为0、10、20、30、40和50 mm。仿真结果如图14所示，包括在不同波浪尺寸条件下液位的测量误差和液位样本方差。

从图14可以看出，波动液位的测量误差将随着波浪尺寸的增加而逐渐增大。然而，当波浪尺寸从0变化到30 mm时，测量误差非常小且几乎不变。即使波浪尺寸达到 50 mm，测量误差也仅为 −1.28 mm。这表明所提出的方法能够克服传统方法的不足，在一定波浪尺寸的液位条件下实现预期的测量误差。与测量误差不同，样本的方差与波浪尺寸密切相关，并随波浪尺寸的增大而增加。后一点意味着，当使用传统方法且超声波束照射到波动液位的波峰或波谷时，可能会产生较大的误差。

IV. 使用真实系统的验证

A. 真实系统的搭建

我们构建了一个真实系统来验证该方法的可行性。该真实系统由三部分组成：1）前端硬件；

2）个人计算机（PC）控制软件；以及3）测量容器。真实系统的框图如图15所示。前端硬件主要由超声换能器阵列和电路板单元组成。换能器阵列由八个相同的圆形换能器构成，直径为12毫米。换能器的中心频率为300千赫兹，带宽约为120千赫兹。根据上述换能器阵列设计方案，所形成的线性阵列长度达到282毫米。换能器阵列安装在钢制支架上，其表面垂直于液位。电路板单元包括八个通道的发射/接收（T/R）电路、T/R开关、任意波形发生器、现场可编程门阵列（FPGA）和微控制器单元（MCU）。在 FPGA的控制下，任意波形发生器输出调频连续波（FMCW）波形。经过宽带脉冲变压器放大后，调频连续波信号被发送到相应的发射换能器。此外，波形发生器还可以产生其他信号波形，如矩形脉冲、正弦脉冲、正交信号和相位编码信号，以便我们在后续工作中研究使用不同发射信号时提出的方法。所有接收通道均由前置放大器 AFE5805、运算放大器、时间增益控制放大器和模数转换器组成。前置放大器构成低噪声放大器、电压控制衰减器、可编程增益放大器和低通滤波器。FPGA控制整个前端硬件，包括波形生成、信号发射/接收和数据采集。此外，FPGA还控制MCU进行数据存储并将数据传输至PC。前端硬件通过通用串行总线与PC连接。相关软件采用C++编写，用于实现相应的控制功能。需要强调的一点是，T/R 通道的带宽超过5兆赫兹。该设计旨在通过使用线性换能器阵列，利用提出的方法进一步开展超声成像研究。

载波频率为3.5兆赫兹。前端数据采集的电路板单元照片如图16所示。为简化设计，测量容器仅为一个尺寸为0.8 m × 0.6 m × 0.5 m的矩形塑料桶。实验测量中的完整系统如图17所示。

B. 动态液位检测

我们首先实现了静态液位保持恒定情况下的波动液位的检测。通过使用吹风机垂直吹拂液面来形成液位波动，且不影响液位测量。通过控制吹风机的风速，可以获得两种不同尺寸的波浪。因此，在强波动和弱波动情况下，液位波幅分别约为10毫米和5毫米。换能器阵列表面到静态液位的距离设置为850毫米，根据波束角宽度，液位上的超声辐射区域近似为600毫米 × 300毫米的矩形区域。

具有正确时间延迟。(b) 无时间延迟)

超声换能器的虚拟换能器在液位数据采集中接收到的实际信号如图18所示。图19显示了带有和不带时间延迟的合成信号的脉冲压缩波形。实验结果与仿真结果一致。脉冲压缩后的波形再次清楚地表明，波束成形技术可以提高接收信号信噪比，且时域中最常用的方法能够满足我们的需求。

对于每种波浪尺寸，我们每隔约一分钟进行一次液位检测，共重复20次。采用液位估计值及其误差绝对值来评估提出的方法。此外，还将提出的方法与传统方法进行了比较。为了保持两种方法的实验条件相同，我们仍采用虚拟单元 $x_{2,1}$ 或 $x_{3,4}$ 的回波信号作为传统方法所接收的回波信号。两种方法得到的液位估计值及其误差绝对值如图20所示。

图20 清楚地表明，在采用所提出的方法进行两次波浪液位检测时，差异不大

液位估计和 (b) 绝对误差)

该方法的最大误差低于1.2 mm。然而，对于传统方法而言情况则不同。使用传统方法时，测量误差可能随着液位波幅的增大而增加，最大误差分别达到约3.016 mm和 4.821 mm。这些事实再次表明，液位波幅对提出的方法影响较小。另一方面，液位估计的算术平均值表明，传统方法通过重复执行液位检测可获得预期结果。但这种简单方法在雨量监测器的应用中可能受到限制，因为在降雨过程中测量容器内的液位是随机变化的。实际液位测量的验证表明，我们的方法在动态液位的瞬时测量方面优于传统方法。

为进一步验证提出的方法在雨量测量中的可靠性，有必要模拟真实环境中液位的动态变化。首先，根据历史气象数据确定每分钟最大降雨量为38 mm。然后分别模拟对应暴雨和中雨的两种液位变化：一种是液位在1分钟内上升 40 mm，另一种是上升20 mm。此外，在液位每增加10% 时进行一次数据采集。同时，仍使用吹风机吹动液面以产生液位波动，所产生的大和小波浪尺寸分别对应暴雨和中雨。另外，容器中的水位高度固定为400 mm，换能器阵列表面到液面的起始距离为600 mm。在液位检测中，实测声速为349.6 m/s。该雨量测量仿真的结果如图21所示。

同样，本节也将传统方法与提出的方法进行了对比。

根据图21，测量结果有利于提出的方法。在相同的降雨条件下，提出的方法将始终精确跟踪液位的变化，而传统方法可能会产生较大的误差。

和(b)分别为液位估计，(c)和(d)分别为绝对误差，对应(a)和(c)的大雨以及(b)和(d)的中雨)

在某些液位处的误差。显然，在中雨条件下，采用提出的方法和传统方法的最大绝对误差分别为1.255 mm和3.68 mm。此外，在暴雨条件下，这两种方法对应的最大误差分别为1.276 mm和6.28 mm。这些实验结果进一步说明，即使在最恶劣的降雨条件下，提出的方法仍能保证精度，而传统方法的性能会随着降雨量增加而下降。因此，该验证不仅表明提出的方法能够在极端条件下胜任精确雨量测量，而且再次证明其在动态变化液位测定方面优于传统的信号通道方法。

V. 结论

本文提出了一种利用相干MIMO超声系统检测动态变化液位的方法。文中总结了该方法的相关方面，如 MIMO阵列的物理结构、发射的FMCW信号模式、收发信号方案、信号处理等。尽管该方法在系统架构上与其他领域的MIMO检测系统相似，但采用了不同的信号处理方式，以适应大目标起伏界面的检测。根据压缩信号的幅度，提出了一种在数字波束形成中对正确焦位进行自适应搜索的方法。这确保了水‐气界面上每个采样点的误差较小，从而保证了测量结果的高精度。基于虚拟阵元技术，设计了换能器阵列，大幅降低了系统的复杂性和成本。此外，本文还基于超声散射理论和边界层理论，提出了一种新的液位回波信号仿真方法。通过该回波信号仿真方法，可以对提出的方法进行全面验证和评估。

仿真和实际实验表明，与传统的单通道方法相比，所提出的方法在动态变化液位情况下能够实现高精度。与采用相控阵技术的扫描方法相比，该方法具有低成本和低复杂性的优势。这使得它除了在动态变化液位检测之外，在其他一些实际应用中也极具吸引力。此外，通过仿真研究了影响所提出方法的相关因素，如焦距位置、接收信号信噪比和液位波幅。然而，仿真结果证明，这些因素对所提出方法的影响小于对传统方法的影响。

在提出的方法中，采用了一种在数字波束形成中自适应搜索正确焦位的方法，以实现对水‐气界面每个采样的高精度。由于该方法依赖于每个潜在聚焦位置处压缩后合成信号的幅度，这种自适应搜索正确焦位的过程可能会影响提出方法的实时性，但通过使用高速电子芯片、合理设计信号处理的硬件系统架构、适当减少液位采样数量等措施，这一问题将大大减轻。对于换能器阵列结构，虚拟阵元技术可实现虚拟相控阵，尽管其他换能器阵列结构也可用于实现MIMO检测系统。这将有助于通过与真实相控阵检测系统进行比较，全面评估所提出方法的性能。此外，我们的回波信号仿真方法与现有方法有显著不同。通过我们的方法仿真的回波信号更接近实际从液位接收到的信号，这为超声波液位检测研究，特别是对动态变化的液位检测，提供了一种新的途径。至于影响因素，液位波幅应被重点考虑。在我们的研究中，当波浪尺寸的增加超过一定程度时，所提方法的精度会明显下降。在这种情况下，有必要采用简单的机械装置来减小液位波幅，以确保可靠的精度。

尽管我们的动机是通过超声波提高雨量测量的精度，但该方法在许多有前景的应用中都是可取的。这种基于 MIMO的超声波换能器阵列结构不需要机械控制，因此可以应用于传统方法不适用的一些环境。例如，该方法可能适用于气象观测中的积雪覆盖、防洪减灾中的河流水位监测，以及水泥和采矿行业中的料位计。此外，通过在换能器阵列的垂直方向增加另一个换能器阵列，可以进一步提高提出的方法的测量精度。

该提出的方法已验证可实现对动态变化的液位进行精确检测，但这仅是初步演示。与提出的方法相关的某些方面尚未进行研究。例如，当采用该方法时，可采用何种信号处理方法来提升其性能在强噪声和干扰环境下如何实现准确检测？此外，可以采用什么技术来减少由于被测目标的速度和加速度引起的距离模糊问题？这些与所提出方法相关的方面将纳入我们未来的工作中。