强化学习&MPC——（三）

这一次来由浅入深认识一下价值函数以及动态规划解决优化问题
首先我们要理解一下状态价值函数，这是bellman equation的第一次正式推导。

trajectory

作为一个trajectory，必须是一个完整的过程，也就是状态转移全部过程，从其实状态到终止状态，没有什么状态是达不到的，只是每种状态都会有代价或者是收益而已。

这里就展示了几条不同的trajectory，注意哈，trajectory可以是像第三种那样的有多条方向的

return

累计奖励是根据一条trajectory得到的，也就是说，针对每一种trajectory都会有一个return，它就是评价我的trajectory好不好的一种方式。所以说到这里，trajectory有点像策略的意思了。

$v_i$

反应一个trajectory好不好，当然就是用到v价值函数了。
$v_1=r_1+\gamma r_2+{\gamma }^2{r}_3+\cdots$
$v_2=r_2+\gamma r_3+{\gamma }^2{r}_4+\cdots$
$v_3=r_3+\gamma r_4+{\gamma }^2{r}_1+\cdots$
$v_4=r_4+\gamma r_1+{\gamma }^2{r}_2+\cdots$
其实可以看的出来，他和return没有什么区别。它就是return存在的意义。
接下来做一个递归：
$v_1=r_1+\gamma r_2+{\gamma }^2{r}_3+\cdots =r_1+\gamma v_2$
$v_2=r_2+\gamma r_3+{\gamma }^2{r}_4+\cdots =r_2+\gamma v_3$
$v_3=r_3+\gamma r_4+{\gamma }^2{r}_1+\cdots =r_3+\gamma v_4$
$v_4=r_4+\gamma r_1+{\gamma }^2{r}_2+\cdots =r_4+\gamma v_1$
写成矩阵的形式就是：
$\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]=\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]+\gamma P\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]$
简写为：
$v=v+\gamma Pv$
其实也就是两部分，即时奖励和未来奖励。

$G_t$

考虑一条trajectory：

这里看起来是确定的action和reward，但是也可以是有转移概率的：

$p(r|s,a)$

位于状态s，采取动作a后的奖励r的概率

$p(s^{\prime }|s,a)$

位于状态s，采取动作a后的状态s’的概率
当然，计算的$G(t)$用不到，它本身就是上面v函数的一个表示：
$G(t)=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+cdots$
这个其实也是累计奖励。return和v函数和它有什么区别呢？下面介绍状态价值函数

$V_{\pi }(s)$

这里开始深入强化学习的本质了，所有的价值函数都不是用来玩的，状态价值看似只与状态有关，其实隐含着与策略有关，甚至可以写成是$v(\pi ,s)$，所以不要再觉得它没用了。
价值函数的定义式非常简单：
$v_{\pi }(s)=\mathbb{E}[G_t|S_t=s]$
也就是处于状态s时的累计奖励。千万注意它是基于策略的函数，不同的策略会得到不同的价值函数，这样我们就能评价策略的好坏
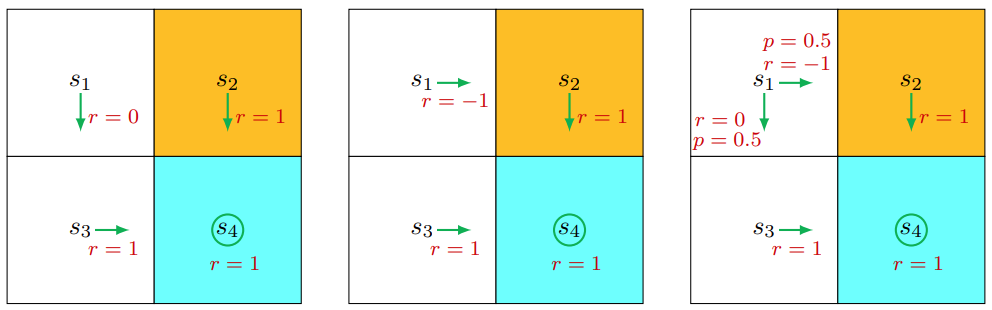
以下是一个具体的例子：

怎么说呢，如果策略是确定的，那么就只与s有关，但是如果是在选在策略的过程中，价值函数是一直都在变化的。

状态价值函数与bellman equation

状态价值函数可以进一步表示，将累计奖励$G_t$迭代展开：

这样我们求的就变成了两个期望，期望就是加权平均，先看左边的式子，就是从状态s出发得到的r的期望，我们把它转化为标准的状态s,动作a的格式，并且引入在状态s动作a时的奖励概率来消除期望符号：

右边的式子也是一样的，主要目标是消除掉期望符号，于是通过状态转移概率来化简：

然后综合两者就得到了bellman公式了：

概率部分是模型，红色的是我们要求的价值函数，策略是用来评价的，所以计算时也是给定的。
以上就完成了bellman公式的分析过程。