强化学习&MPC——（二）

本篇主要介绍马尔科夫决策（MDP）过程，在介绍MDP之前，还需要对MP，MRP过程进行分析。

马尔科夫性质

马尔可夫性是指一个系统，在给定当前状态的情况下，未来的状态仅依赖于当前状态，而不依赖于过去的状态。换句话说，当前状态包含了过去所有状态的信息，因此未来的状态可以完全由当前状态决定。说白了就是带遗忘性质，下一个状态S_t+1仅与当前状态有关，而与之前的状态无关。

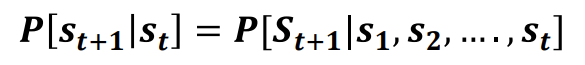
为什么需要马尔科夫性——简化环境模型。帮助强化学习来学习。
这种性质对于建模环境至关重要，因为它简化了问题的复杂性，并且使得我们能够用一个简洁的方式描述系统的动态演化。在强化学习中，马尔可夫性质的存在使得我们可以使用MDP来建模智能体与环境的交互，从而进行有效的决策和学习。

什么是马尔可夫过程（MP）

马尔科夫过程：通过状态转移概率的实现的过程，马尔科夫过程是一个**<S,P>**，S是有限状态集合，P是状态转移概率。
马尔可夫过程是指一个满足马尔可夫性质的随机过程。一个马尔可夫过程由状态空间$S$和状态转移概率矩阵$P$组成。状态转移概率矩阵$P$表示了从一个状态转移到另一个状态的概率。

什么是马尔可夫奖励过程（MRP）

马尔科夫奖励过程：马尔可夫奖励过程是在马尔可夫过程的基础上增加了奖励的概念。一个马尔可夫奖励过程由状态空间$S$、状态转移概率矩阵$P$和奖励函数$R$组成。奖励函数$R$定义了在特定状态转移过程中，智能体会获得的即时奖励。
在马尔可夫过程的基础上增加奖励函数R和衰减系数γ,基本上一谈到奖励就会有折扣因子的存在。表示为 （S,P,R,γ）。
$S$ 是状态空间；
$P$ 是状态转移概率矩阵，表示从一个状态转移到另一个状态的概率；
$R$ 是奖励函数，表示在状态转移过程中智能体会获得的即时奖励。
对于一个马尔可夫奖励过程，我们可以定义一个状态的预期奖励，即在特定状态下智能体未来可能获得的奖励的期望值。状态$s$的预期奖励可以表示为：

其中，$R_t$是在时间步$t$时智能体获得的即时奖励，$\gamma$是折扣因子。

R是一个奖励函数，S状态下的奖励是某一时t处在状态s下在下一个时刻（t+1）能获得的期望奖励。

期望的含义也就是说与概率是相关的，求概率平均。
累计回报：从t时刻所得到的折扣回报总和。折扣因子表示了对未来奖励的重视程度。越小就是越短视，越大就越远视。

价值函数：价值函数给出了某一状态或某一行为的长期价值。
状态价值函数和动作价值函数来看待问题（强化学习最重要的公式）

注意这里的价值函数可能是状态价值，也可以是动作价值

马尔科夫一个重要的内容就是要通过bellman方程求解状态价值函数。
如何求解？
n比较小时直接计算，n比较大时通过迭代来求解：

• 动态规划
• 蒙特卡洛评估
• 时序差分学习
  最后就是马尔科夫决策过程MDP了，由（SAPRγ）五元组成。

什么是马尔科夫决策过程？

状态动作，状态转移概率，回报函数，折扣因子
状态（State）：描述环境可能处于的各种情况。
动作（Action）：智能体可以采取的行动。
状态转移概率（State Transition Probability）：描述在采取特定行动后，环境会转移到下一个状态的概率。
奖励函数（Reward Function）：描述智能体在特定状态下采取特定行动所获得的即时奖励。
折扣因子（Discount Factor）：用于衡量未来奖励的重要性，通常表示为γ（gamma）。
我们可以使用数学符号来表示MDP。假设我们有一个状态空间（State Space）$S$，动作空间（Action Space）$A$，状态转移概率函数$P$，奖励函数$R$，以及折扣因子$\gamma$。MDP可以表示为元组$(S,A,P,R,\gamma )$。

在MDP中，我们通常会遇到两种主要的函数：状态转移函数和奖励函数。状态转移函数$P$定义了从一个状态到另一个状态的转移概率，可以表示为：

其中，$s_t$表示当前状态，$a_t$表示采取的动作，$s_{t+1}$表示下一个状态。
奖励函数$R$定义了在给定状态和动作的情况下，智能体会获得的即时奖励，可以表示为：

在强化学习中，我们的目标是学习一个策略（Policy），即智能体在特定状态下选择动作的方式。通常，我们会使用价值函数（Value Function）来评估状态或状态-动作对的好坏程度。常见的价值函数包括状态值函数（State Value Function）$V(s)$ 和动作值函数（Action Value Function）$Q(s,a)$。

MDP就引入了policy的概念，策略是决定行为的机制。强化学习的本质就是最优策略的寻找。
策略同样是仅与当前状态有关。可以是随机策略或者确定性策略。

两大价值函数的引入：
状态值函数（State Value Function）$V(s)$ 衡量了在给定策略（Policy）下，智能体处于状态$s$时所能获得的预期回报（Expected Return）。换句话说，它描述了从当前状态开始，智能体在未来可能获得的累积奖励。

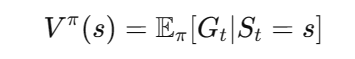
其中，$G_t$ 表示从时间步$t$开始的累积奖励，$\pi$ 是策略函数，表示智能体在特定状态下采取的动作。

展开如下所示：

动作值函数（Action Value Function）$Q(s,a)$ 衡量了在给定策略（Policy）下，智能体处于状态$s$并采取动作$a$时所能获得的预期回报（Expected Return）。换句话说，它描述了在当前状态下采取特定动作后，智能体未来可能获得的累积奖励。

其中，$G_t$ 表示从时间步$t$开始的累积奖励，$\pi$ 是策略函数，表示智能体在特定状态下采取的动作。

推导如下所示：

最优理论就是关于价值函数的：
从所有策略产生的状态价值函数中，选取使状态s价值最大的函数：

从所有策略产生的行为价值函数中，选取是状态行为对 价值最大的函数:

状态值函数的贝尔曼方程
对于状态值函数$V^{\pi }(s)$，其贝尔曼方程可以表示为：

其中，$\pi (a|s)$ 表示在状态$s$下选择动作$a$的概率，$p(s^{\prime },r|s,a)$ 表示在状态$s$采取动作$a$后，转移到状态$s^{\prime }$并获得奖励$r$的概率，$\gamma$ 是折扣因子。
推导如下：

动作值函数的贝尔曼方程
对于动作值函数$Q^{\pi }(s,a)$，其贝尔曼方程可以表示为：

其中，$p(s^{\prime },r|s,a)$ 表示在状态$s$采取动作$a$后，转移到状态$s^{\prime }$并获得奖励$r$的概率，$\pi (a^{\prime }|s^{\prime })$ 表示在状态$s^{\prime }$下选择动作$a^{\prime }$的概率，$\gamma$ 是折扣因子。
推导如下：

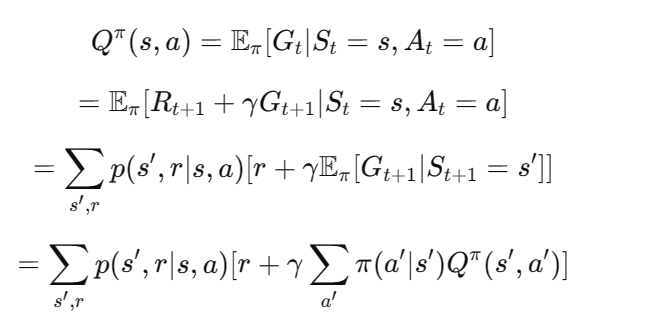
下次我们将先从价值函数出发分析问题，然后通过动态规划算法解决优化问题的思路。

后续内容：
线性mpc
包括等式约束和不等式约束
非线性mpc
构建优化问题
泰勒展开线性化
KKT条件处理不等式约束
求解SQP问题

一些重要参数
预测窗口
终端项

预见性的控制（优化问题与控制效果）

SQP解决MPC的优化问题。（解一个序列控制量问题）

另一种求解思路：
HJB方程。
成本函数-状态方程——哈密顿函数
转为泛函优化问题：
变分法，分部积分，求极点的思路。
构造哈密尔顿函数
状态方程，协状态方程
控制最优条件 终值和初值条件

线性模型+二次型优化问题。
求解黎卡提方程。