基于无人机的移动传感器定位算法

使用无人机的移动无线传感器网络定位

摘要

定位是无线传感器网络中最重要的方面之一。文献中提出的大多数定位算法适用于静态网络。然而，这些协议在移动环境中的性能仍有待研究。由于节点的移动性，在移动环境中进行定位可能面临精度和计算复杂度方面的挑战。
本文提出了一种使用无人机的移动无线传感器网络定位算法（LMWSND）。
提出了一种基于无人机的算法来模拟无人机的移动轨迹。该基于无人机的算法利用无人机与未知传感器节点之间的接收信号强度技术来确定它们之间的距离。所获得的距离用于未知节点的定位。本文采用一种新方法求解距离方程组，以限制误差传播。此外，对LMWSND中误差传播的数学分析证明了我们所提出算法相较于其他算法的优越性。仿真结果进一步证实了我们的结论，即所提出的算法能够减少误差传播。我们还提出了另一种算法，用于选择附近的信标点，以更好地利用网络资源并降低计算开销。

1 引言

无线传感器网络（WSNs）由大量广泛分布的微小且轻便的无线传感器节点组成，这些节点被大量部署以监测环境或测量物理现象，如压力、温度、相对湿度、物体运动等。这些传感器节点在硬件上成本低廉、体积小、功能多样、感知能力强，并能够在短距离内进行通信。这些节点可以形成一个多跳、分布式和自组织的无线通信网络。
如今，无线传感器网络（WSNs）已广泛应用于灾害检测与管理、灾后搜救行动、目标跟踪、复杂地形的远程控制、环境预测和检测、库存管理、精准农业等领域。在这些应用中，大多数都需要事件发生地点的位置坐标，因为若不了解位置信息，与该地点、物体或事件相关的数据可能无法使用。因此，位置估计或定位成为无线传感器网络（WSNs）各种应用的基本需求。

查找传感器节点位置的最简单方法是使用全球定位系统（GPS）。但是，在基于GPS的方法中，传感器节点必须配备GPS接收器硬件。除了需要额外的硬件外，GPS还存在其他缺点，例如在室内环境中可用性受限。GPS的最佳应用环境是开放环境，在该环境中可以轻松与卫星通信。为了克服上述GPS的缺点，研究人员设计了许多定位算法。然而，设计能够在最小硬件、最小通信成本和有限功率条件下工作的定位算法是一项具有挑战性的任务。因此，由于这些限制，文献中已由研究人员提出了多种针对无线传感器网络（WSNs）的定位算法。这些定位算法在设计时考虑了多种因素，如计算模型、GPS、范围估计和可扩展性。这些算法的主要目标是通过最小化定位误差（LE）或距离误差来提高定位精度。

文献中已经讨论了许多定位算法来估计未知节点的位置。这些算法使用了多种技术，例如飞行时间、到达时间、接收信号强度指示（RSSI）等。但这些技术存在噪声、多径衰落和信号反射等问题。DV‐Hop是一种用于无线传感器网络（WSN）中基于跳数信息进行定位的算法。尽管DV‐Hop算法实现简单，但其定位精度较差。该算法需要一定数量的锚节点（位置已知的节点）来确定未知节点的位置。因此，锚节点数量越多，算法的定位精度越高。然而，大量节点作为锚节点会增加网络成本，因为锚节点需要配备GPS。长期以来，许多研究人员提出了对DV‐Hop算法的改进方法，以提高其定位精度。因此，为了在不降低定位精度的前提下减少锚节点的数量，同时克服各种技术的不足并避免使用GPS，本文提出了一种用于移动无线传感器网络中的新型定位算法。在我们所提出的定位算法中，结合了无人机和接收信号强度指示技术。本研究的主要贡献包括以下几点：
- 我们使用无人机对未知节点进行定位，而不是使用GPS。
- 建议一种算法来模拟无人机的路径。
- 在移动过程中，未知节点的定位通过利用通信半径内的信标点的接收信号强度来实现。这减少了通信次数，从而降低了能量消耗。
- 提出了一种新方法来求解距离方程组，以减小误差传播。
- 还对误差传播进行了数学分析。

本文的其余部分安排如下。第2节讨论了相关工作，包括移动模型在DV‐Hop中的应用。第3节阐述了所提出的方案。第4节给出了所提算法中误差传播的数学分析，并与现有算法进行了比较。第5节展示了仿真工作和结果。最后，第6节对本文的工作进行了总结。

2 相关工作

文献中已提出多种用于空中网络的路由框架。在参考文献25中，Kumar等人提出了一种用于无人机辅助通信网络框架的空中网络自组织移动模型。该模型能够估计在无人机辅助子网内或子网间两个无人机之间建立连接的概率。他们还在文献中提出了一种路由选择算法，以选择最短路径。D‐IoT26是一种物联网环境中的无人机辅助分布式路由框架。该作者提出的模型重点关注高度动态的飞行环境。该模型的整体框架基于无人机，其中采用神经模糊推理系统来选择可靠且高效的路由。文献中已提出多种定位算法。在参考文献27中，作者提出了一种基于到达角（AOA）和接收信号强度指示（RSSI）的混合定位算法，以实现无线传感器网络中的更好定位。该算法还对AOA和RSSI进行了误差分析。该算法对完全覆盖的兴趣区域内未知节点密度具有免疫性。在具有大型障碍物的地形中，使用RSSI提供的精度相对较低。此外，使用RSSI会导致安全性降低。几何定位算法28是一种用于大规模三维无线传感器网络的无测距定位算法。该算法使用利用移动锚节点对所有静态未知节点进行定位。该方法采用圆形截面选择技术进行定位，但在定位精度方面仍有改进空间。凯瓦尔塔等人29提出了一种基于几何的车载信息物理系统在GPS中断期间的定位算法。该算法通过车辆的历史信息（坐标、方向速度等）以及道路轨迹，在GPS信号中断期间估计车辆的当前位置。然而，由于定位所考虑的几何形状并非如假设的标准几何元素，因此车辆的定位精度仍存在改进空间。这种对几何元素的假设可能导致定位误差传播。

如今，大量研究集中在利用一个或多个移动锚节点进行定位。其中一些研究在此进行了详细讨论：文献34中，Annepu和Rajesh提出了一种用于无人机辅助定位的基于机器学习的算法。作者使用无人机作为移动锚节点，对网络中的静态未知节点进行定位。无人机与静态未知节点之间的通信采用对数正态阴影衰落模型。随后使用多层感知机模型优化目标函数，即定位精度。然而，对数正态阴影衰落模型的应用前提是发射器和接收器之间的路径为无遮挡状态，这在无线传感器网络（WSNs）中极为罕见。此外，该算法复杂度较高，导致节点训练速度较慢。文献35中，作者采用极限学习算法替代多层感知机（MLP），以获得更好的结果，因为节点的训练速度得到了提升。但该模型仍存在对数正态阴影衰落模型的缺陷。文献36中，Yu等人提出了一种利用无人机对安装在列车上的移动终端进行定位的算法。无人机与移动终端之间通过接收信号强度指示（RSSI）建立通信。该算法还考虑了列车的运动状态，从而在无人机与移动终端之间的测得距离上引入了一个补偿因子。该算法采用对数正态阴影衰落方法处理无人机与移动终端之间的RSSI。使用对数正方法忽略了发射器和接收器之间的障碍物影响。

在参考文献37中，作者测试了DV‐Hop算法18在三种移动模型下的性能，即随机路点模型（RWP）38、随机方向模型（RD）39和参考点组移动模型（RPGM）40。他们讨论了移动无线传感器网络（MWSNs），其中锚节点是移动的，而未知节点保持静态。该方法将时间划分为离散时间单位，使得在某一时刻，移动的锚节点被视为静态。锚节点的位置在固定时间间隔内发生变化，因此使用GPS来确认每个时间单位内节点的位置。他们还将DV‐Hop算法应用于MWSNs。因此，通过将DV‐Hop算法与不同的移动模型结合，得到了一组新的定位算法，即DV‐Hop+RWP、DV‐Hop+RD和DV‐Hop+RPGM。这些模型将静态锚节点转变为移动锚节点。DV‐Hop+RWP模型存在一个局限性，即移动锚节点倾向于选择靠近仿真区域中心的下一个目的地，而该区域的节点密度较高。

在DV‐Hop+RPGM模型中，所有节点在一定速度下基于随机路点模型在特定范围内移动。组成员随着群组移动而持续移动，并在同一时间到达目的地后全部停止。因此，该模型在考虑群组运动时会放大每个传感器的位置误差，严重地影响定位精度。在DV‐Hop+RD模型中，移动节点沿角度方向朝向仿真区域边界移动。尽管作者应用DV‐Hop算法以保持简单性，但这以牺牲定位精度为代价。GPS的周期性使用也使系统成本更高。这些DV‐Hop的变体同样存在DV‐Hop算法的常见缺点，包括跳距误差，该误差会传播到锚节点与未知节点之间估计距离的过程中。此外，由于求解距离方程组所采用的方法，该误差进一步被传播。因此，定位精度仍有改进空间。

3 移动无线传感器网络中使用无人机的定位：一种提出的算法

在本文中，我们提出了一种利用无人机进行移动无线传感器网络定位的算法（LMWSND）。其工作原理如图1所示。

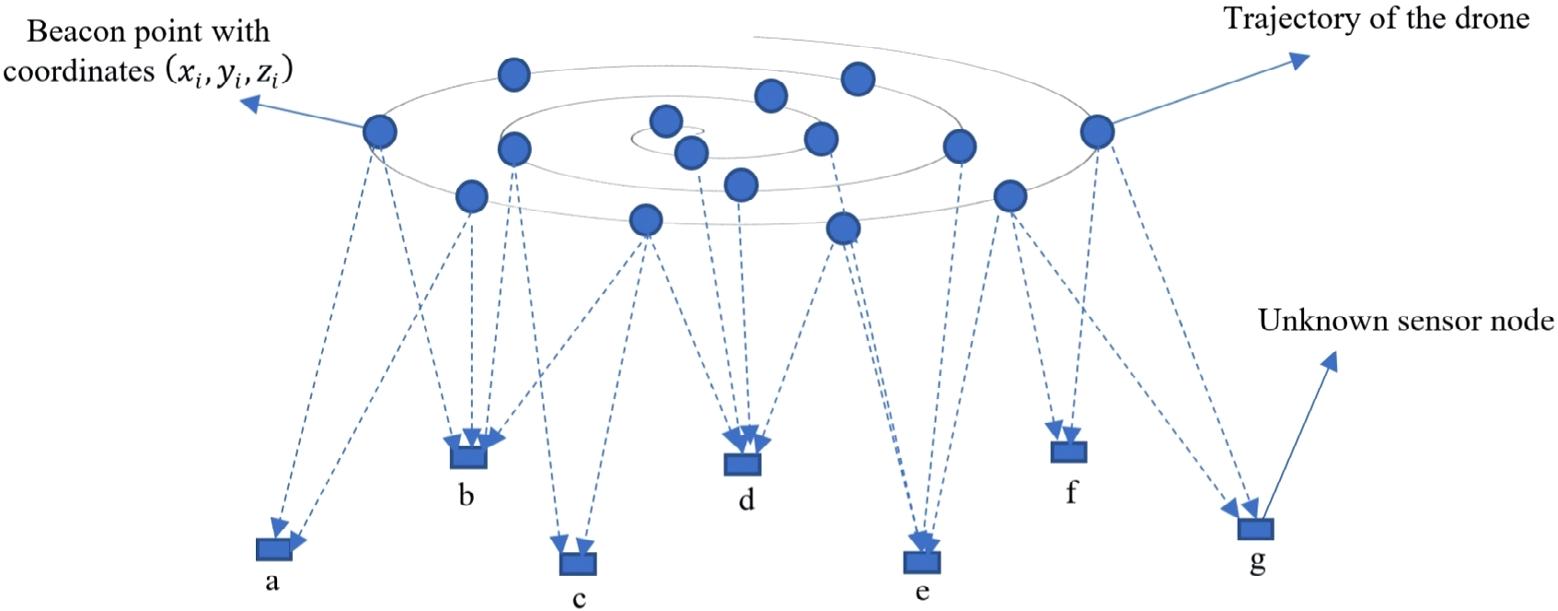
图1展示了无人机的轨迹和信标点。信标点包含无人机在轨迹上定期发送信标包的位置坐标。它还展示了未知节点u如何利用附近信标点的接收信号强度指示（RSSI）来确定其位置。因此，该算法包含三个步骤。

步骤1

在所提出算法的这一步中，无人机沿使用算法1定义的路径行进。无人机选择螺旋路径，以实现最大覆盖范围。此外，无人机在其行进路径上发送信标包。算法1选择信标包的广播频率。该频率还取决于网络的密度。对于密集网络，信标包的广播频率或时间间隔较高，而在稀疏网络中则降低。

算法1. 无人机仿真
初始化：
1. 信标间隔：发送信标包的时间间隔
2. 路径：无人机从仿真区域中心到区域边界或相反方向的螺旋运动
3. 速度：无人机的速度
4. t：定时器，t根据网络密度进行设置。如果网络稀疏，可以较长；如果网络密集，t必须较小。

开始：
5. 过程 飞行路径 ()
6. 重复 直到所有节点都已定位
7. 当 完整路径被遍历时
8. 广播 (xd,yd,zd) 在 t 之后
9. 结束当
10. 结束重复
11. 结束过程

步骤2

在此步骤中，首先，我们根据信标点和未知节点的接收信号强度指示选择最近的信标点。这减少了能量消耗，因为我们并未使用网络中所有节点的接收信号强度指示。此外，未知节点u使用双向传播模型来计算未知节点u与信标点之间的距离。

附近信标点的选择

我们使用算法2来选择用于距离计算的信标包。仅选择信号强度大于阈值RSSI的最近信标点。这减少了计算开销，因为只分析有限数量的信标点，而不是无人机轨迹上的所有信标点。未知节点需要至少四个信标点的位置，以通过多边定位法计算该节点的坐标。

算法2：选择通信范围内的信标包
初始化：
1. RSSI：接收信号强度指示。
2. MinRSSI：阈值RSSI。
3. BeaconPoints：无人机路径上的信标点，从这些位置发送信标包。
4. N：位于未知节点通信范围内的信标点数量

5. 对于 每个未知节点
6. 如果 (RSSI >= MinRSSI) 则
7. 选择 传感器节点通信范围内的信标点
8. 如果 (N >= 4) 则
9. 返回 该未知节点
10. 结束如果
11. 结束如果
12. 否则 等待无人机的反向路径仿真。
13. 结束对于

传感器节点使用接收信号强度指示（RSSI）来计算自身与无人机之间的距离。此外，我们采用双射线地面模型41来计算距离，如公式(1)所示。该传播模型有助于将信号强度转换为距离。当接收到信标包时，传感器节点可以测量接收信号强度，然后利用该传播模型计算节点与信标点之间的距离。我们选择双射线地面传播模型，以做出更符合实际的假设，该模型考虑了来自地面的信号反射。

$$
d= \sqrt{\frac{4PtGtGrh_t^2 h_r^2}{Pr}}
\tag{1}
$$

其中Gr是未知节点上接收天线的增益，Gt是无人机上发射天线的增益，hr是未知节点上接收天线的高度，ht是无人机上发射天线的高度，Pt是无人机的发射功率，以及Pr是未知节点的接收功率。

步骤3

在此步骤中，我们将网络中所有未知节点的运动转换为离散时间间隔。在非常短的时间间隔内，节点被视为静态。在此小时间间隔内，利用步骤2中计算的距离以及从步骤1接收到的信标点坐标，对未知节点进行定位。为了估计未知节点的位置，我们假设未知节点u的坐标(x, y, z)，第n个信标点的位置为(xn, yn, zn)，dn表示使用公式(1)计算出的第n个信标点与未知节点u之间的距离。在公式(2)中，我们列出了未知节点u到附近信标点的距离方程。

$$
\begin{cases}
\sqrt{(x -x_1)^2+(y -y_1)^2+(z -z_1)^2}= d_1 \
\sqrt{(x -x_2)^2+(y -y_2)^2+(z -z_2)^2}= d_2 \
\vdots \
\sqrt{(x -x_m)^2+(y -y_m)^2+(z -z_m)^2}= d_m \
\vdots \
\sqrt{(x -x_n)^2+(y -y_n)^2+(z -z_n)^2}= d_n
\end{cases}
\tag{2}
$$

设第m个信标点距离未知节点u最远，该距离为dm。为了简化公式(2)，我们对两边取平方，如公式(3)所示。

$$
\begin{cases}
(x -x_1)^2+(y -y_1)^2+(z -z_1)^2= d_1^2 \
(x -x_2)^2+(y -y_2)^2+(z -z_2)^2= d_2^2 \
\vdots \
(x -x_m)^2+(y -y_m)^2+(z -z_m)^2= d_m^2 \
\vdots \
(x -x_n)^2+(y -y_n)^2+(z -z_n)^2= d_n^2
\end{cases}
\tag{3}
$$

现在将最大距离方程从其余方程中减去，并将所得方程除以最大距离方程，如公式(4)所示

$$
\begin{cases}
\frac{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2 −((x−x_1)^2+(y−y_1)^2+(z−z_1)^2)}{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2} = \frac{d_m^2−d_1^2}{d_m^2} \
\frac{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2 −((x−x_2)^2+(y−y_2)^2+(z−z_2)^2)}{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2} = \frac{d_m^2 −d_2^2}{d_m^2} \
\vdots \
\frac{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2 −((x−x_n)^2+(y−y_n)^2+(z−z_n)^2)}{(x−x_m)^2+(y−y_m)^2+(z−z_m)^2} = \frac{d_m^2 −d_n^2}{d_m^2}
\end{cases}
\tag{4}
$$

进一步简化公式(4)，我们得到

$$
\begin{aligned}
&2(x_1d_m^2 −x_md_1^2)x + 2(y_1d_m^2 −y_md_1^2)y + 2(z_1d_m^2 −z_md_1^2)z = d_m^2 s − d_1^2 s+ d_m^2(x_1^2 +y_1^2 + z_1^2) − d_1^2(x_1^2 +y_1^2 + z_1^2) ,\
&2(x_2d_m^2 −x_md_2^2)x + 2(y_2d_m^2 −y_md_2^2)y + 2(z_2d_m^2 −z_md_2^2)z = d_m^2 s − d_2^2 s+ d_m^2(x_2^2 +y_2^2 + z_2^2) − d_2^2(x_2^2 +y_2^2 + z_2^2) , \
&\vdots \
&2(x_nd_m^2 −x_md_n^2)x+ 2(y_nd_m^2 −y_md_n^2)y+ 2(z_nd_m^2 −z_md_n^2)z= d_m^2 s − d_n^2 s+ d_m^2(x_n^2+y_n^2+ z_n^2) − d_n^2(x_n^2+y_n^2+ z_n^2) ,
\end{aligned}
\tag{5}
$$

其中，$ s=x^2+y^2+z^2 $

$$
\begin{aligned}
&2(x_1d_m^2 −x_md_1^2)x + 2(y_1d_m^2 −y_md_1^2)y + 2(z_1d_m^2 −z_md_1^2)z = d_m^2 s − d_1^2 s+ d_m^2(x_1^2 +y_1^2 + z_1^2) − d_1^2(x_1^2 +y_1^2 + z_1^2) ,\
&2(x_2d_m^2 −x_md_2^2)x + 2(y_2d_m^2 −y_md_2^2)y + 2(z_2d_m^2 −z_md_2^2)z = d_m^2 s − d_2^2 s+ d_m^2(x_2^2 +y_2^2 + z_2^2) − d_2^2(x_2^2 +y_2^2 + z_2^2) , \
&\vdots \
&2(x_nd_m^2 −x_md_n^2)x+ 2(y_nd_m^2 −y_md_n^2)y+ 2(z_nd_m^2 −z_md_n^2)z= d_m^2 s − d_n^2 s+ d_m^2(x_n^2+y_n^2+ z_n^2) − d_n^2(x_n^2+y_n^2+ z_n^2) ,
\end{aligned}
\tag{6}
$$

公式(6)中的这些方程组可以写成矩阵方程的形式。

$$
AX= B
\tag{7}
$$

其中，A、X 和 B 定义为

$$
A=
\begin{bmatrix}
2(x_1d_m^2 −x_md_1^2) & 2(y_1d_m^2 −y_md_1^2) & 2(z_1d_m^2 −z_md_1^2) & d_1^2 − d_m^2 \
2(x_2d_m^2 −x_md_2^2) & 2(y_2d_m^2 −y_md_2^2) & 2(z_2d_m^2 −z_md_2^2) & d_2^2 − d_m^2 \
\vdots & \vdots & \vdots & \vdots \
2(x_nd_m^2 −x_md_n^2) & 2(y_nd_m^2 −y_md_n^2) & 2(z_nd_m^2 −z_md_n^2) & d_n^2 − d_m^2 \
\end{bmatrix}
,
$$

$$
B=
\begin{bmatrix}
(d_1^2 − d_m^2)(x_1^2+y_1^2+ z_1^2) \
(d_2^2 − d_m^2)(x_2^2+y_2^2+ z_2^2) \
\vdots \
(d_n^2 − d_m^2)(x_n^2+y_n^2+ z_n^2) \
\end{bmatrix}
,
$$

$$
X=
\begin{bmatrix}
x \
y \
z \
s \
\end{bmatrix}.
$$

通过求解方程(7)采用平方方法，未知节点的位置Z通过以下方程获得。

$$
Z=(A^TA)^{-1}A^TB
\tag{8}
$$

因此，为了实现MWSN的定位，我们整理了LMWSND在所有时间间隔内的结果。这些时间间隔被转换为连续时间，并连续应用所提出的算法来定位网络中的未知节点（表1）。

TABLE 1 符号表

符号	描述
d	传感器节点与无人机之间的距离
dn	nth个信标点与未知节点之间的距离
Gr	未知节点上接收天线的增益
Gt	无人机上发射天线的增益
Pt	无人机的发射功率
Pr	传感器节点的接收功率
ht	无人机上发射天线的高度
hr	传感器节点上接收天线的高度
(x,y,z)	未知节点的坐标
(xn,yn,zn)	第n个信标点的坐标
(xm,ym,zm)	距离最大的信标点的坐标
en	距离dn的误差
R	传感器节点的通信半径
N	传感器节点总数
M	信标点总数
## 4 求解方程组中误差传播的数学分析
众所周知，使用双射线地面模型计算的距离由于采用了估计方法和外部参数而包含固有误差。当我们求解距离方程组时，该误差会进一步迅速传播。通过数学分析，我们证明了与现有定位算法相比，我们所提出算法中的误差传播更小。

我们有一个距离方程组，表示如下

$$
\begin{cases}
\sqrt{(x -x_1)^2+(y -y_1)^2+(z -z_1)^2}= D_1 \
\sqrt{(x -x_2)^2+(y -y_2)^2+(z -z_2)^2}= D_2 \
\vdots \
\sqrt{(x -x_m)^2+(y -y_m)^2+(z -z_m)^2}= D_m \
\vdots \
\sqrt{(x -x_n)^2+(y -y_n)^2+(z -z_n)^2}= D_n
\end{cases}
\tag{9}
$$

设Dm为最大距离方程。

由于多径衰落、地面反射和噪声等各种外部参数，这些距离 D1, D2,…Dm…Dn存在误差。设这些距离 D1, D2, …Dm…Dn的误差分别为 e1, e2…em…en。因此，我们将这些距离 D1,D2…Dm…Dn表示为：

$$
\begin{cases}
D_1= d_1+ e_1 \
D_2= d_2+ e_2 \
\vdots \
D_m= d_m+ e_m \
\vdots \
D_n= d_n+ e_n
\end{cases}
\tag{10}
$$

其中，d1, d2…dm…dn为实际距离。

在DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法中，为求解公式(9)给出的方程组，我们对距离方程两边进行平方，然后将所有方程从最后一个距离方程（第n个）中减去，使其线性化。设所有方程均从距离dn中减去。
根据参考文献42，我们有值A= a ± Δa和B= b ± Δb，其中a、b是实际值，而 Δa、Δb是误差项。

如果，A′=A²
然后，A′中的误差传播表示为

$$
ΔA′= 2a ∗ Δa
\tag{11}
$$

因此，当我们对公式(9)中的距离方程进行平方时，公式(10)中D²i和D²n的误差传播为

$$
\begin{cases}
ΔD′_i = 2d_i e_i \
ΔD′_n= 2d_n e_n
\end{cases}
\tag{12}
$$

实际值分别为 d²i 和 d²n。

此外，通过使用参考文献42，让我们从A中减去B，即A−B，那么传播误差为 √(Δa²+ Δb²)。

因此，将所有这些平方方程从最后一个距离方程（第n个）中相减，传播误差由以下方程表示。

$$
ΔD= \sqrt{(2d_n e_n)^2+(2d_i e_i)^2} \quad \forall i= 1, 2…n−1,
$$

$$
ΔD= 2\sqrt{d_n^2 e_n^2+ d_i^2 e_i^2}
\tag{13}
$$

误差的实际值为d²i −d²n，因此DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD中的误差传播由公式(13)表示。在所提出的方法中，我们将最大距离方程的平方减去该方程的平方后所得结果除以最大距离方程的平方。

现在设，A′′= A∕B
通过使用参考文献42，当我们用A除以B时，误差传播变为

$$
ΔA′′= \frac{a}{b}\sqrt{\left(\frac{Δa}{a}\right)^2+\left(\frac{Δb}{b}\right)^2}
\tag{14}
$$

因此，所提出的方法中的误差传播由以下方程给出。

$$
ΔD′=\frac{(d_m^2 − d_i^2)}{d_m^2} \sqrt{ \left(\frac{2\sqrt{d_m^2 e_m^2+ d_i^2 e_i^2}}{(d_m^2 − d_i^2)}\right)^2 +\left(\frac{2d_m e_m}{d_m^2}\right)^2 }, \quad \forall i= 1, 2…n−1, \text{ and } i≠ m,
$$

$$
ΔD′= \frac{2}{d_m^3}\sqrt{ 2d_m^2 e_m^2(d_m^2 − d_i^2)+ d_i^2(d_i^2 e_m^2+ d_m^2 e_i^2)}
$$

设，$ p^2= \frac{d_i^2}{d_m^2} $

$$
ΔD′= \frac{2}{d_m}\sqrt{ e_m^2(1−p^2)+p^2(p^2 e_m^2+ e_i^2) }
\tag{15}
$$

现在，我们需要证明我们的方法中的误差传播小于DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法中的误差传播。

因此，我们证明了， ΔD′ <ΔD 由公式(13)可得，

$$
ΔD= 2\sqrt{d_n^2 e_n^2+ d_i^2 e_i^2 },
$$

$$
ΔD= 2d_m e_m\sqrt{\left(\frac{d_n e_n}{d_m e_m}\right)^2 +\left( \frac{d_i e_i}{d_m e_m}\right)^2},
\tag{16}
$$

0 < ei < em 和 0 < en < em 或 0 < di ei < dm em 和 0 < dn en < dm em

$$
0< \frac{d_n e_n}{d_m e_m} < 1 \quad \text{and} \quad 0< \frac{d_i e_i}{d_m e_m} < 1 \quad \text{OR} \quad 0<\left( \frac{d_n e_n}{d_m e_m}\right)^2 < 1 \quad \text{and} \quad 0<\left( \frac{d_i e_i}{d_m e_m}\right)^2 < 1
$$

$$
\max\left[\left(\frac{d_n e_n}{d_m e_m}\right)^2 +\left( \frac{d_i e_i}{d_m e_m}\right)^2\right]= 2 \quad \text{因此，}
$$

$$
ΔD= 2d_m e_m\sqrt{2}, \quad ΔD= 2\sqrt{2}d_m e_m
\tag{17}
$$

方程(15)变为

$$
ΔD′= \frac{2e_m}{d_m} \sqrt{ 2−2p^2+p^4+p^2 \frac{e_i^2}{e_m^2} }
\tag{18}
$$

设， $ 1+p^2\frac{e_i^2}{e_m^2} = q^2 $

因此，方程 (18) 变为

$$
ΔD′= \frac{2e_m}{d_m} \sqrt{ (1−p^2)^2+ q^2 }
\tag{19}
$$

我们知道，dm>1，因此， $ \frac{d_i^2}{d_m^2} < 1 $

p² < 1 therefore, max[p²] ≅ 1
dm ≥ di ∀i= 1, 2…n−1
dm是最大距离。因此，dm的误差大于其他di的误差。由于，em>ei因此，

$$
\frac{e_i^2}{e_m^2} < 1 \quad \text{and} \quad p^2 \frac{e_i^2}{e_m^2} < 1
$$

由于p² ei²/em²的最大值可以是1。

因此，

$$
1+p^2 \frac{e_i^2}{e_m^2} \leq 2 \quad \text{hence, } 1< q^2 \leq 2 \quad \text{and max}[q^2]= 2.
$$

现在从公式(17)到(19)，

$$
\frac{ΔD′}{ΔD}= \frac{ \frac{2e_m}{d_m} \sqrt{(1−p^2)^2+ q^2} }{ 2\sqrt{2}d_m e_m } = \frac{ \sqrt{(1−p^2)^2+ q^2} }{ d_m^2 \sqrt{2} }
\tag{20}
$$

由于，d²m ≫ 1.22 那么，

$$
\frac{1.22}{d_m^2} \ll 1 \quad \text{且} \quad \frac{ΔD′}{ΔD} \ll 1 \quad \text{因此，} \quad ΔD′ <<ΔD
$$

这证明了我们的LMWSND方法中的误差传播小于DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法。

5 仿真结果与性能分析

本节将所提出的算法与DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法的效率进行了比较。为了评估性能，所提出的算法在MATLAB中进行了仿真。DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD均为DV‐Hop的变体，其中DV‐Hop针对三种不同的移动模型进行研究，因此在仿真中，我们将DV‐Hop变体中的锚节点视为所提出算法中的信标点，并将无人机视为移动锚节点。此外，性能分析中的定位误差（LE）由公式(21)定义。

$$
\text{Localization error}= \frac{ \sum_{n=M+1}^{N} \sqrt{(x_{nu} −x_{na})^2+(y_{nu} −y_{an})^2+(z_{nu} −z_{an})^2} }{ R \times(N −M) }
\tag{21}
$$

其中（xnu,ynu, znu)为第n个未知节点的估计坐标，(xna,yan,zan)为该未知节点的实际坐标。N表示网络中未知传感器节点的总数，M决定信标点的数量，R表示节点的通信半径。由于未知节点的定位误差（LE）与定位精度成反比，因此 LE值越低，定位精度越高。在现实场景中，使用接收信号强度指示（RSSI）方法测量距离时总存在一定的误差，因此估计值与理论值之间总会存在差异，这种差异称为RSSI误差。为了模拟真实场景，RSSI误差考虑了两个范围： 0%到10%和10%到20%。

为了评估定位误差（LE）的性能，进行了实验。通过这些实验，观察了节点总数、信标点百分比、通信半径、无人机高度、无人机密度、无人机覆盖整个网络所需的轮数以及移动性对定位误差的影响。仿真结果已在第5.1至 5.7小节中进行了分析。

在实验仿真中，我们考虑了一个100 m×100 m ×100 m的立方区域，其中节点被随机部署。在所有仿真中，所有其他参数对所有算法保持一致。此外，每种算法均在随机生成的场景下运行1000次，各项指标的值取平均后进行比较。表2定义了用于仿真的所有必要参数。

TABLE 2 参数表

参数	值
无人机参数
无人机速度	10 米/秒
广播间隔（t）	1/秒
无人机最佳高度	50 m
未知节点数量	400
最小高度和最大高度	10 和 130 米
双向地面传播模型参数
发射器/无人机的功率（Pt）	− 39 dBm
接收器/未知节点的功率（Pr）	− 30 dBm
发射天线增益 (Gt)	6.55
接收天线增益 (Gr)	4.55
接收天线高度 (hr)	1 m
发射天线高度 (ht)	15 m
通信半径 (R)	15 m
传感器节点速度	1米/秒
RSSI误差	0%‐10%, 10%‐20%

缩写：RSSI，接收信号强度指示。

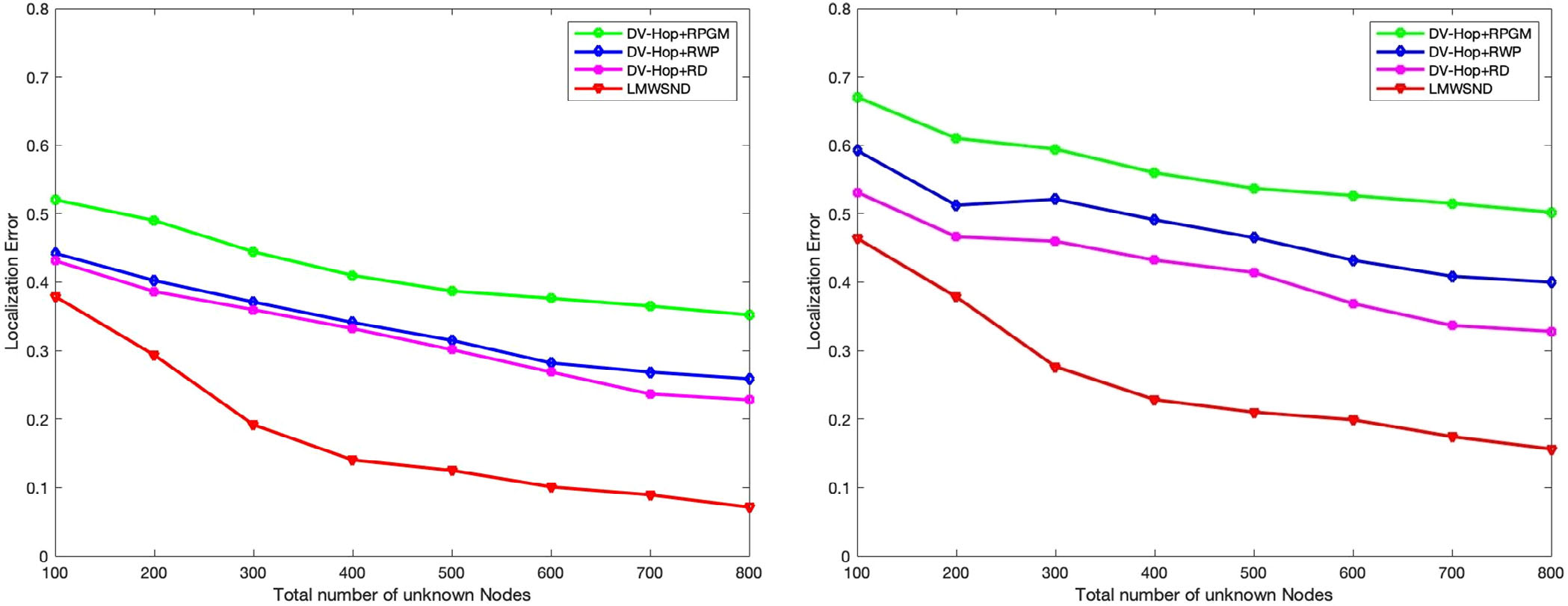
(A) 未知节点总数 Vs. 接收信号强度指示误差为0‐10%时的定位误差
(B) 未知节点总数 Vs. 接收信号强度指示误差为10‐20%时的定位误差

5.1 未知节点总数对定位误差的影响

图2A、B显示了在RSSI误差分别为0%到10%和10%到20%的情况下，网络中传感器节点总数（与未知节点数相同）的变化对定位误差的影响。信标点百分比保持在15%，通信半径为15米，节点总数从100变化到800。

从图2A、B的结果可以看出，随着节点数量的变化，LMWSND的定位误差小于DV‐Hop+RPGM、DV‐Hop+ RWP和DV‐Hop+RD。与LMWSND相比，DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD的定位误差下降较慢。在100到400个节点范围内，LMWSND的定位误差变化斜率非常明显。LMWSND的定位误差总体下降约30%，而DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD的定位误差仅下降15%至20%。

5.2 信标点百分比对定位误差的影响

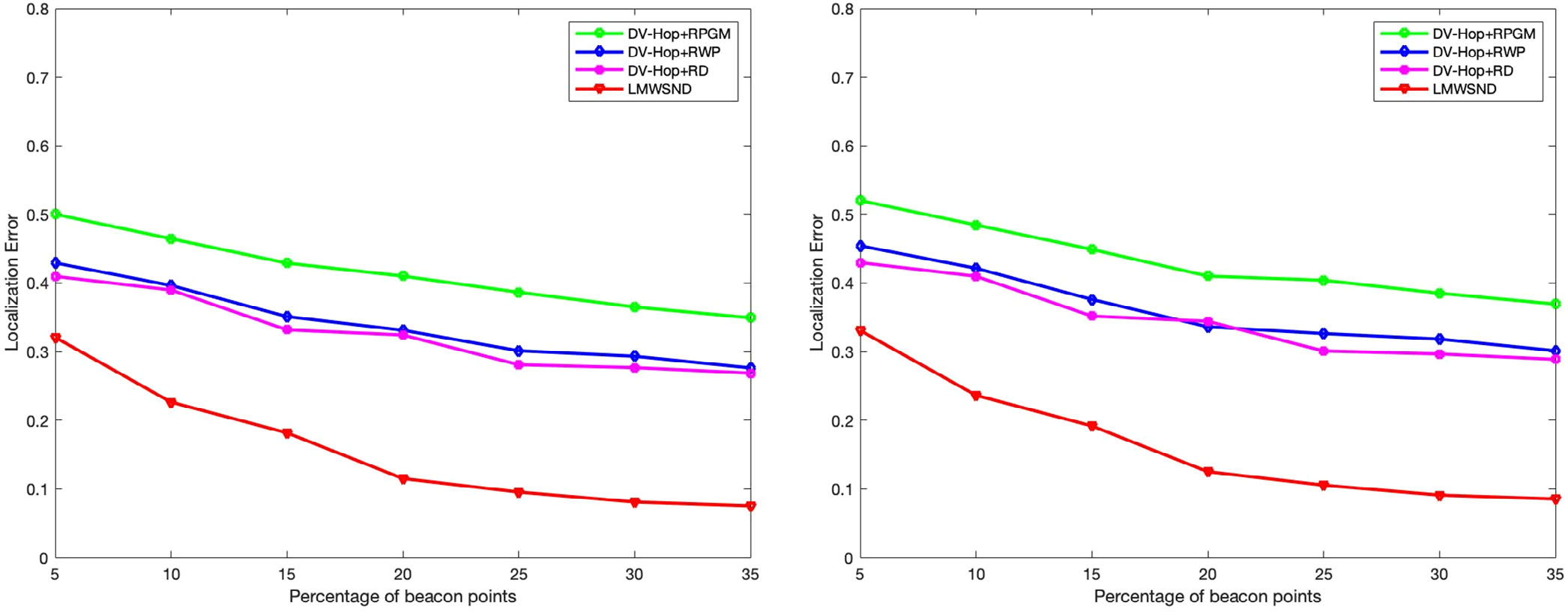
(A) 信标点百分比 Vs. 接收信号强度指示误差0‐10%时的定位误差
(B) 信标点百分比 Vs. 接收信号强度指示误差10‐20%时的定位误差

图3A,B展示了信标点百分比变化对定位误差的影响，其中RSSI误差分别在0%到10%和10%到20%范围内。网络中的节点总数保持恒定为400，通信半径为15米。信标点百分比从5%变化到35%。

从结果可以看出，对于每个信标点百分比的取值，LMWSND 的定位误差均小于 DV‐Hop+RPGM、DV‐Hop+RWP 和 DV‐Hop+RD。当信标点从 5% 增加到 20% 时，LMWSND 的定位误差急剧下降；此后，定位误差的下降趋于平稳。在信标点达到 35% 时，LMSWND 的定位误差降低了约 20% 至 25%，而 DV‐Hop+ RPGM、DV‐Hop+RWP 和 DV‐Hop+RD 的定位误差仅降低约 5% 至 10%。当信标点百分比超过 20% 后，定位误差随着信标点百分比的增加趋于稳定。

5.3 通信半径对LE的影响

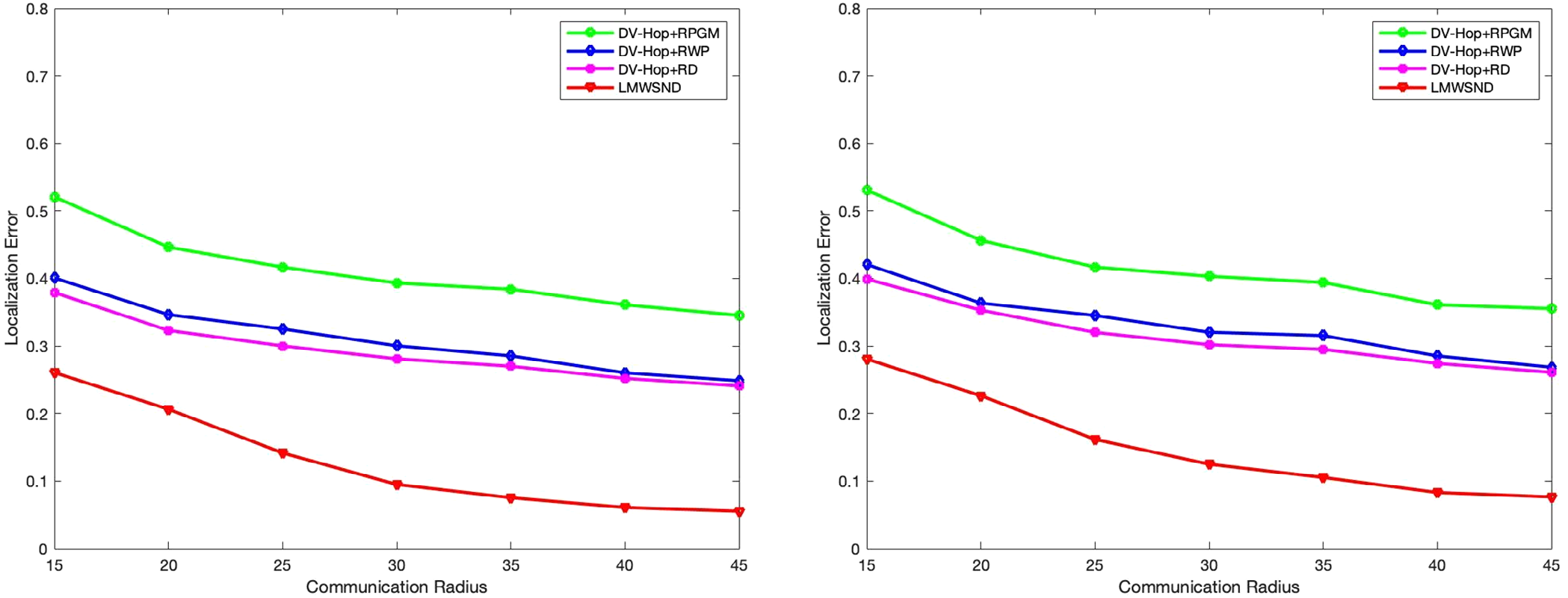
(A) 通信半径 Vs. RSSI误差为0‐10%时的定位误差
(B) 通信半径 Vs. RSSI误差为10‐20%时的定位误差

图4A,B所示结果表明，对于相同的通信半径值，LMWSND的定位误差（LE）小于DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法。当通信半径从15米增加到30米时，LMWSND的LE下降更为显著，而当通信半径从30米增加到45米时，LE值趋于稳定。与DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法相比，LMWSND的LE总体减少了约25%。

5.4 无人机高度对定位误差的影响

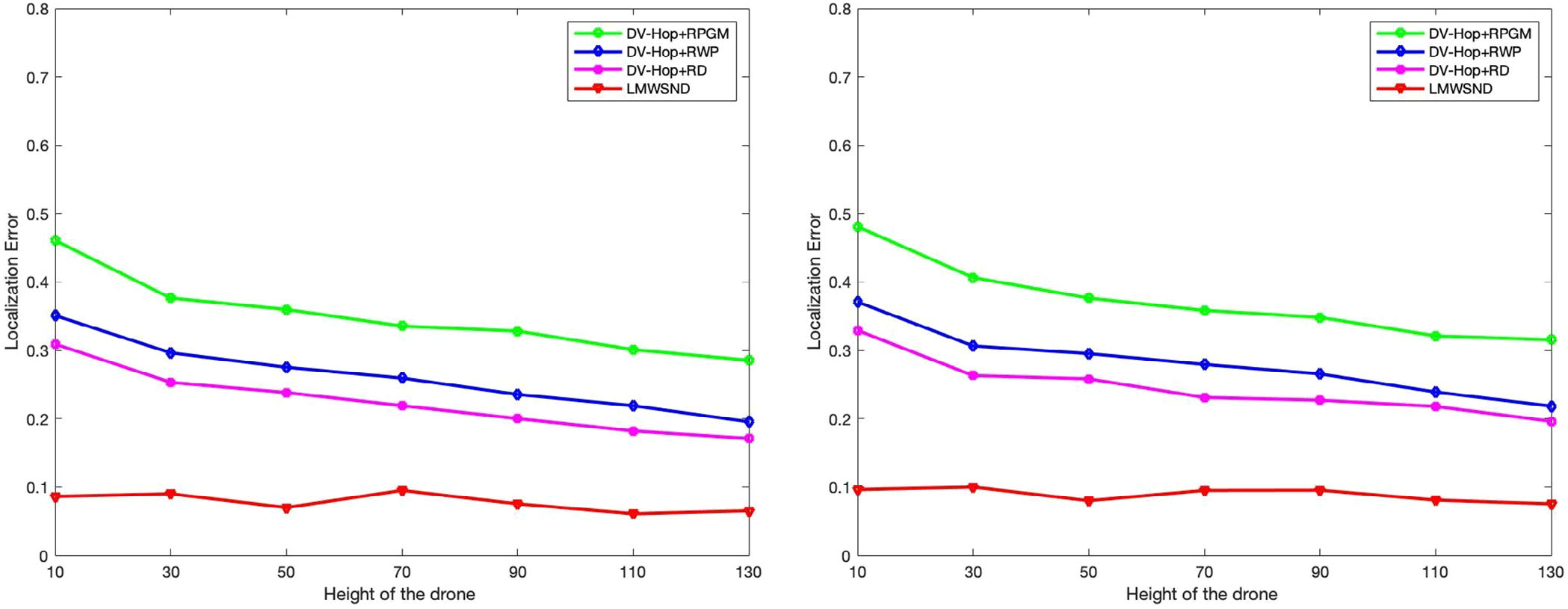
(A) 无人机高度 Vs. 定位接收信号强度指示误差 0‐10% 的定位误差
(B) 无人机高度 Vs. 定位接收信号强度指示误差 10‐20% 的定位误差

图5A,B显示了无人机高度变化对定位误差的影响，其中RSSI测距误差分别为0%到10%和10%到20%。信标点百分比随高度在15%到45%范围内变化，通信半径为15米。无人机高度从10米变化到110米。由于所考虑的模型是三维模型，因此z轴表示高度。

从图5A,B所示的结果中我们观察到，对于不同高度的无人机，LMWSND的定位误差相较于DV‐Hop+ RPGM、DV‐Hop+RWP和DV‐Hop+RD更小。DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD的定位误差相比LMWSND下降较慢。我们所提出算法的定位误差平均值保持在10%以下，而其他对比算法则超过25%。在仿真所考虑的受限环境中，当高度为50m时定位误差最小，表明该高度为无人机的最佳高度，此时大多数未知节点得以定位。

5.5 无人机密度对定位误差的影响

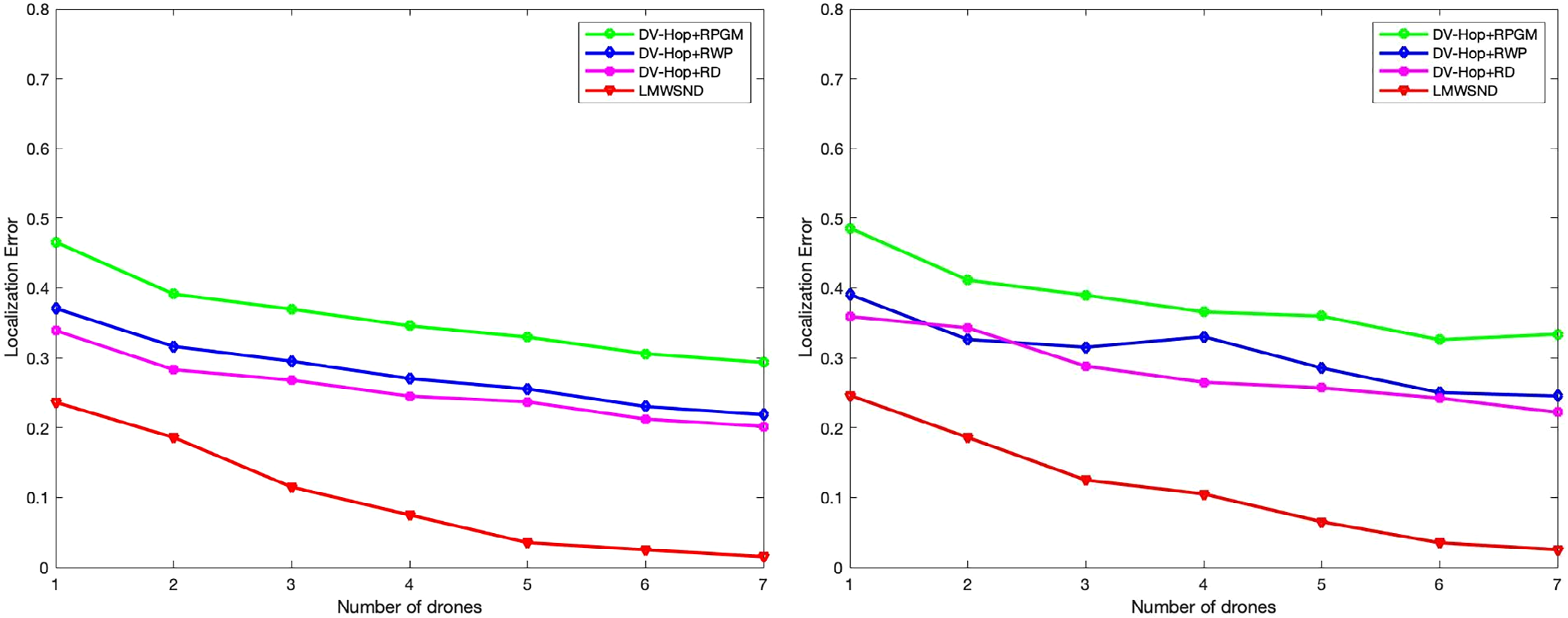
(A) 无人机数量与定位RSSI误差0‐10%时的定位误差
(B) 无人机数量与定位RSSI误差10‐20%时的定位误差

图6A,B显示了由于无人机密度变化导致的LE变化，其中RSSI分别在0%到10%和10%到20%范围内。随着无人机数量的增加，信标点数量显著增加。传感器节点的通信半径保持恒定在15米，节点总数为400。这还导致了无人机覆盖区域的增加，从而提高了定位精度，即LE降低。与DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法相比，LMWSND在定位精度上表现出显著提升。在受限的仿真环境中，通过仿真我们观察到，当无人机数量达到五架时，定位精度似乎趋于稳定。此后，进一步增加无人机数量时，LE仅有微小下降。因此，五架无人机是实现网络中所有节点定位的最佳数量，能够在取得最佳效果的同时降低成本，相较于七架无人机更具优势。LMWSND的表现也优于其他对比算法，其LE差异从使用一架无人机时的15%增加到使用七架无人机时的23%。

5.6 无人机覆盖整个网络所需轮数对定位误差的影响

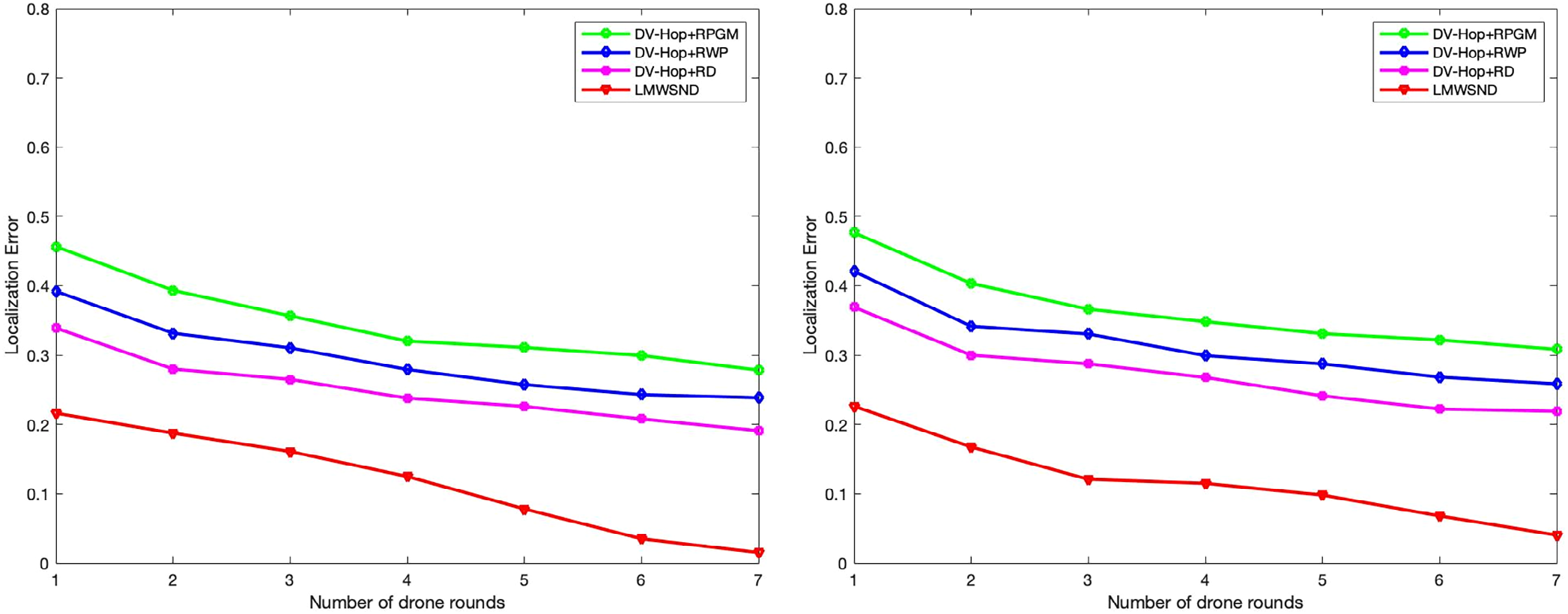
(A) 无人机轮数 Vs. RSSI误差为0‐10%时的定位误差
(B) 无人机轮数 Vs. RSSI误差为10‐20%时的定位误差

图7A,B展示了无人机为覆盖整个网络所需的完整绕行圈数。它描绘了在RSSI误差范围为0%到10%和10%到20%时，每完成一圈无人机飞行后定位误差（LE）的变化情况。网络中无人机数量保持为1，未知节点的通信半径为15米，网络中的节点总数保持恒定为400。

图7A,B显示，通过无人机平均飞行七轮后，由于信标点频率直接增加，网络中几乎所有未知节点都被成功定位。每增加一轮无人机飞行，未知节点的定位精度都有显著提升。该图还详细说明了在无人机飞行轮数相同的情况下，LMWSND相较于DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法表现更优。在第一轮时，所提算法的定位精度分别比DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法高出13%、18%和26%。而在第七轮后，LMWSND的定位精度相比DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+RD算法分别提高了17%、22%、28%。

5.7 移动性对定位误差的影响

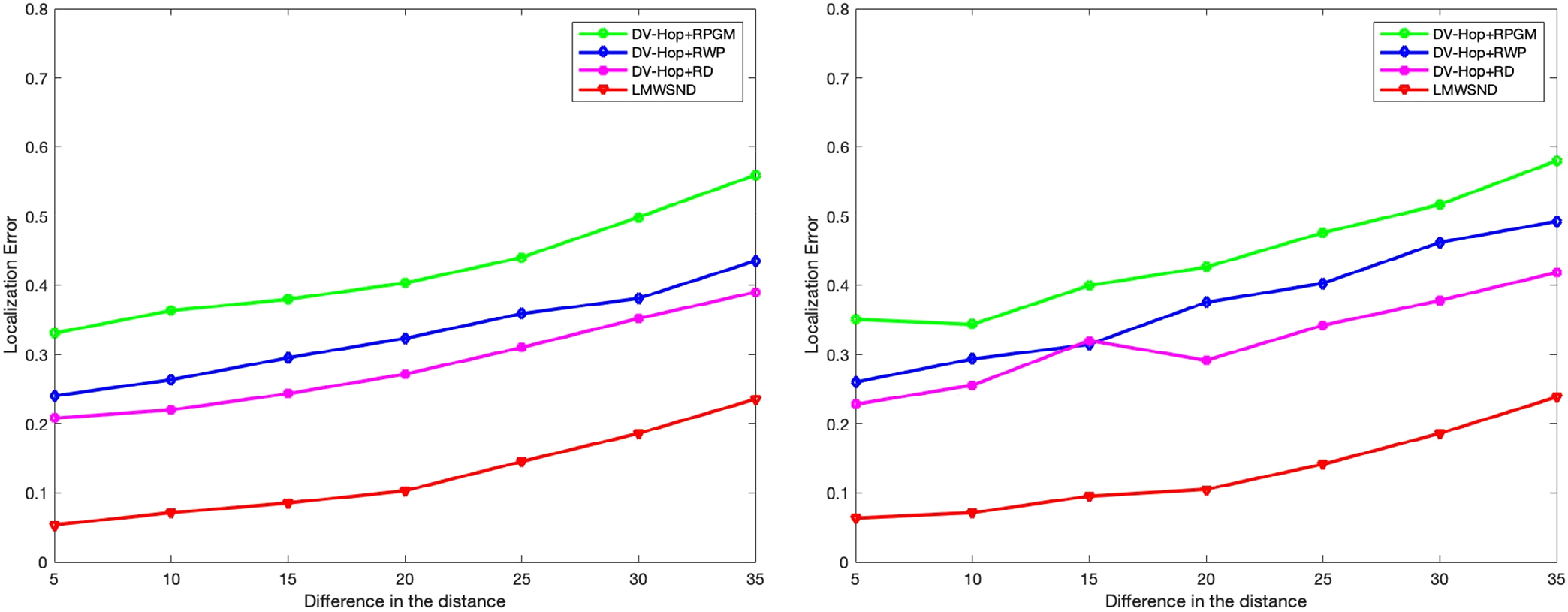
(A) 传感器节点的移动性 对比 0‐10% RSSI误差下的定位误差
(B) 传感器节点的移动性 对比 RSSI误差10‐20%时的定位误差

为了分析传感器节点移动性的影响，我们采用了随机游走移动模型（RWP）38来模拟网络中传感器节点的运动。在仿真过程中，传感器节点以1米/秒的速度移动。图8A、B展示了从参考点的距离差异，即传感器节点的移动性对定位精度的影响，其中RSSI误差范围分别为0%到10%和10%到20%。无人机数量限制为1架，传感器节点的通信半径保持恒定为15米，网络中的节点总数限制为400。随着与参考点距离差异的增加，定位误差也随之上升。在节点移动初期，LMWSND的定位误差分别为15%、18%和27%，相较于DV‐Hop+RPGM、DV‐Hop+RWP和DV‐Hop+ RD算法。

6 结论

在本研究工作中，我们提出了一种利用无人机对MWSNs进行定位的定位算法。在所提出的算法中，无人机被用作锚节点来估计移动节点的位置。该模型通过避免节点与超出范围的节点进行不必要的通信，从而节约了能量。同时，由于减少了通信次数，也实现了对带宽等网络资源的更优利用。此外，我们采用一种新方法求解距离方程组，从而降低了误差传播。针对LMWSND的误差数学分析证明，与其他现有算法相比，我们的算法具有显著更小的误差。
仿真结果显示，与其它现有算法相比，我们的算法将定位误差（LE）降低了约20%至30%。