空间代数
空间代数是一种在刚体动力学中常用的数学符号体系,用于表示和处理诸如速度、加速度和力等物理量。Pinocchio库就是基于这种数学符号体系构建的。它提供了专门的类来表示三维欧几里得空间中的坐标变换(命名为SE3)、空间运动向量(Motion)、空间力向量(Force)以及空间惯性(Inertia)。结合可用的方法,这使得Pinocchio成为一个高效的空间代数计算软件库。
模型与数据
Pinocchio的一个基本范式是严格区分 “模型” 和 “数据”。这里的 “模型” 指的是机器人的物理描述,包括定义其结构的运动学参数,可能还包括惯性参数。这些信息由一个专门的类来保存,一旦创建,Pinocchio的算法不会对其进行修改。而 “数据” 指的是所有计算结果的值。“数据” 会根据系统的关节配置、速度等因素而变化,例如,它包含每个连杆的速度和加速度。它还存储算法的中间计算结果和最终结果,以避免内存分配。通过这种划分,Pinocchio中的所有算法都遵循以下签名:
algorithm(model, data, arg1, arg2, ...)
其中arg1, arg2, ...是函数的参数(例如配置或速度)。在对同一机器人执行多个不同任务时,尤其是涉及并行计算时,保持模型和数据的分离可以减少内存占用。每个进程可以使用自己的数据对象,同时共享相同的模型对象。在Pinocchio的算法中,模型对象始终保持不变,这增强了代码的可预测性。
可以使用C++ API创建模型,也可以从外部文件加载模型,这些文件可以是URDF、Lua(遵循RBDL标准)或Python格式。
关节
在一个模型中,机器人被表示为一个运动学树,它包含所有关节的集合、关节连接信息,以及可选的与每个连杆相关的惯性量。在Pinocchio中,一个关节可以有一个或多个自由度,并且它属于以下类别之一:
- 旋转关节:围绕固定轴旋转,该轴可以是(X)、(Y)、(Z)轴之一,也可以是自定义轴;
- 棱柱关节:沿固定轴平移,与旋转关节类似;
- 球形关节:在三维空间中自由旋转;
- 平移关节:在三维空间中自由平移;
- 平面关节:在二维空间中自由运动;
- 自由浮动关节:在三维空间中自由运动。平面关节和自由浮动关节通常用作移动机器人(如人形机器人、自动驾驶汽车或操作规划中的物体)运动学树的基础。
- 通过 “复合” 关节的概念,可以将多个普通关节组合成更复杂的关节。
注:在URDF格式中,可以定义 “固定” 类型的关节。然而,“固定” 关节实际上并不是真正的关节,因为它不能移动。出于效率考虑,它被视为模型的操作框架。
从关节到李群几何
每种类型的关节都有其特定的配置空间和切空间。例如,旋转关节的配置空间和切空间都是实数轴(R\mathbb{R}R),而球形关节的配置空间对应于三维旋转矩阵的集合,其切空间是三维实向量空间(R3\mathbb{R}^{3}R3)。有些配置空间可能不具备向量空间的性质,但必须赋予相应的积分(指数映射exp)和微分(对数映射log)算子。Pinocchio实现了所有这些特定的积分和微分算子。
有关此主题的更多内容,请参见 “处理李群几何”。
几何和碰撞模型
除了运动学模型,Pinocchio还定义了几何模型,即附着在运动学树上的体积。这个模型可用于显示机器人以及计算与碰撞相关的量。与运动学模型类似,固定的量(体积的位置和形状)存储在 “GeometricModel” 对象中,而相关算法使用的缓冲区和量则在另一个对象中定义。体积使用FCL库进行表示。机器人的各个部分附着在每个关节上,而环境中的障碍物则在世界坐标系中定义。基于FCL方法,实现了运动学树的碰撞和距离算法。
处理李群几何
Pinocchio在很大程度上依赖李群和李代数来处理运动,尤其是旋转。因此,它支持以下特殊群(SO(2)SO(2)SO(2))、(SO(3)SO(3)SO(3))、(SE(2)SE(2)SE(2))、(SE(3)SE(3)SE(3)),并实现了它们相关的代数(se(2)\mathfrak{se}(2)se(2))、(se(3)\mathfrak{se}(3)se(3))。
它有多种应用,例如表示机器人自由飞行关节(通常是移动机器人的底座)的运动,或者机器人连杆的运动。后者在碰撞检测中特别有用。
定义李代数的一般向量空间也很有意义。
在C++中使用(SE(2))与Pinocchio
作为一个示例,考虑一个在平面((R2×S1)(\mathbb{R}^2 \times \mathbb{S}^1)(R2×S1))中运动的移动机器人。

机器人从位置(poses=(xs,ys,θs)pose_s = (x_s,y_s,\theta_s)poses=(xs,ys,θs))出发,经过刚性运动(δu=(δx,δy,δθ)\delta_u=(\delta x,\delta y,\delta \theta)δu=(δx,δy,δθ))后,到达位置(poseg=(xg,yg,θg)pose_g = (x_{g},y_{g},\theta_{g})poseg=(xg,yg,θg))。
可以使用以下代码实例化相应的(SE(2)SE(2)SE(2))对象:
typedef double Scalar;
enum {Options = 0};
SpecialEuclideanOperationTpl<2,Scalar,Options> aSE2;
SpecialEuclideanOperationTpl<2,Scalar,Options>::ConfigVector_t pose_s,pose_g;
SpecialEuclideanOperationTpl<2,Scalar,Options>::TangentVector_t delta_u;
可以将Scalar替换为其他类型,如float。
在这个例子中,(poses=(1,1,π/4)pose_s=(1,1,\pi/4)poses=(1,1,π/4)),(poseg=(3,1,−π/2)pose_g=(3,1,-\pi/2)poseg=(3,1,−π/2)),我们想要计算(δu\delta_uδu):
pose_s(0) = 1.0; pose_s(1) = 1.0;
pose_s(2) = cos(M_PI/4.0); pose_s(3) = sin(M_PI/4.0);
pose_g(0) = 3.0; pose_g(1) = -1.0;
pose_g(2) = cos(-M_PI/2.0); pose_g(3) = sin(-M_PI/2.0);
aSE2.difference(pose_s,pose_g,delta_u);
std::cout << delta_u << std::endl;
aSE2用于计算表示两个位姿的配置向量之间的差异。注意,旋转由两个数(sin(θ)sin(\theta)sin(θ))、(cos(θ)cos(\theta)cos(θ))表示,这也是一个(SO(2)SO(2)SO(2))对象。差异存在于(SE(2)SE(2)SE(2))的切空间中,由一个三维实向量表示。
因此,输出为:
3.33216
-1.38023
-2.35619
注意,线性部分并非沿直线运动,它还考虑了系统的旋转。
我们可以通过积分来验证这是正确的运动:
SpecialEuclideanOperationTpl<2,Scalar,Options>::ConfigVector_t pose_check;
aSE2.integrate(pose_s,delta_u,pose_check);
std::cout << pose_check << std::endl;
结果确实是:
3
-1
0
-1
在C++中使用(SE(3))与Pinocchio
假设我们的移动机器人不在平面中,而是在三维空间中。考虑物理空间中的一个物体,我们希望将其从一个位置移动到另一个位置。这里的难点在于物体在三维空间中有六个自由度,其中三个对应平移,三个对应旋转。
同样可以使用相同的算法并更改维度参数来实例化相应的对象,此时是一个(SE(3)SE(3)SE(3))对象:
typedef double Scalar;
enum {Options = 0};
SpecialEuclideanOperationTpl<3,Scalar,Options> aSE3 ;
SpecialEuclideanOperationTpl<3,Scalar,Options>::ConfigVector_t pose_s,pose_g;
SpecialEuclideanOperationTpl<3,Scalar,Options>::TangentVector_t delta_u ;
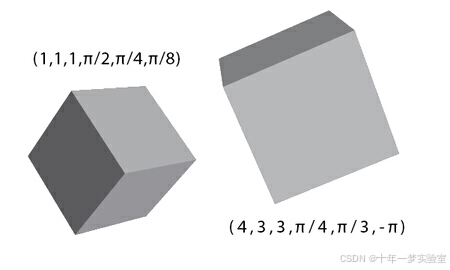
在这个例子中,(poses=(1,1,1,π/2,π/4,π/8)pose_s=(1,1,1,\pi/2,\pi/4,\pi/8)poses=(1,1,1,π/2,π/4,π/8)),(poseg=(4,3,3,π/4,π/3,−π)pose_g=(4,3,3,\pi/4,\pi/3, -\pi)poseg=(4,3,3,π/4,π/3,−π))。对于起始位置,先绕(yyy)轴旋转,然后绕(xxx)轴旋转,最后绕(zzz)轴旋转。对于最终位置,旋转顺序为绕(xxx)轴、(yyy)轴、(zzz)轴。我们想要计算(δu\delta_uδu)。
- 对于第一个位姿,每个旋转都有对应的旋转矩阵:
Rxs=[1000cos(π/8)−sin(π/8)0sin(π/8)cos(π/8)] R_{x_s} = \begin{bmatrix} 1 &0 &0 \\ 0 &cos(\pi/8) &-sin(\pi/8) \\0 &sin(\pi/8) &cos(\pi/8) \end{bmatrix} Rxs=1000cos(π/8)sin(π/8)0−sin(π/8)cos(π/8)
Rys=[cos(π/4)0sin(π/4)010−sin(π/4)0cos(π/4)] R_{y_s} = \begin{bmatrix} cos(\pi/4) &0 &sin(\pi/4) \\ 0 &1 &0 \\-sin(\pi/4) &0 &cos(\pi/4) \end{bmatrix} Rys=cos(π/4)0−sin(π/4)010sin(π/4)0cos(π/4)
Rzs=[cos(π/2)−sin(π/2)0sin(π/2)cos(π/2)0001] R_{z_s} = \begin{bmatrix} cos(\pi/2) &-sin(\pi/2) &0 \\sin(\pi/2) &cos(\pi/2) &0 \\ 0 &0 &1\end{bmatrix} Rzs=cos(π/2)sin(π/2)0−sin(π/2)cos(π/2)0001
因此,完整的旋转矩阵为:
Rposes=Rsz⋅Rsx⋅Rsy=[0−10cos(π/4)⋅cos(π/8)+sin(π/4)⋅sin(π/8)0sin(π/4)⋅cos(π/8)−cos(π/4)⋅sin(π/8)sin(π/8)⋅cos(π/4)−cos(π/8)⋅sin(π/4)0sin(π/4)⋅sin(π/8)+cos(π/4)⋅cos(π/8)] R_{pose_s} = R_{s_z} \cdot R_{s_x} \cdot R_{s_y} = \begin{bmatrix} 0 &-1 &0 \\ cos(\pi/4)\cdot cos(\pi/8) + sin(\pi/4) \cdot sin(\pi/8) &0 &sin(\pi/4) \cdot cos(\pi/8) - cos(\pi/4) \cdot sin(\pi/8) \\ sin(\pi/8) \cdot cos(\pi/4) - cos(\pi/8) \cdot sin(\pi/4) &0 &sin(\pi/4) \cdot sin(\pi/8) + cos(\pi/4) \cdot cos(\pi/8) \end{bmatrix} Rposes=Rsz⋅Rsx⋅Rsy=0cos(π/4)⋅cos(π/8)+sin(π/4)⋅sin(π/8)sin(π/8)⋅cos(π/4)−cos(π/8)⋅sin(π/4)−1000sin(π/4)⋅cos(π/8)−cos(π/4)⋅sin(π/8)sin(π/4)⋅sin(π/8)+cos(π/4)⋅cos(π/8) - 对于第二个位姿,有:
Rxg=[1000cos(π/4)−sin(π/4)0sin(π/4)cos(π/4)] R_{x_g} = \begin{bmatrix} 1 &0 &0 \\ 0 &cos(\pi/4) &-sin(\pi/4) \\0 &sin(\pi/4) &cos(\pi/4) \end{bmatrix} Rxg=1000cos(π/4)sin(π/4)0−sin(π/4)cos(π/4)
Ryg=[cos(π/3)0sin(π/3)010−sin(π/3)0cos(π/3)] R_{y_g} = \begin{bmatrix} cos(\pi/3) &0 &sin(\pi/3) \\ 0 &1 &0 \\ -sin(\pi/3) &0 &cos(\pi/3) \end{bmatrix} Ryg=cos(π/3)0−sin(π/3)010sin(π/3)0cos(π/3)
Rzg=[cos(−π)−sin(−π)0sin(−π)cos(−π)0001] R_{z_g} = \begin{bmatrix} cos(-\pi) &-sin(-\pi) &0 \\ sin(-\pi) &cos(-\pi) &0 \\ 0 &0 &1\end{bmatrix} Rzg=cos(−π)sin(−π)0−sin(−π)cos(−π)0001
完整的旋转矩阵为:
Rposeg=[−cos(π/3)−sin(π/3)⋅sin(π/4)−cos(π/4)⋅sin(π/3)0−cos(π/4)sin(π/4)−sin(π/3)sin(π/4)⋅cos(π/3)cos(π/3)⋅cos(π/4)] R_{pose_g} = \begin{bmatrix} -cos(\pi/3) &-sin(\pi/3) \cdot sin(\pi/4) &-cos(\pi/4) \cdot sin(\pi/3) \\ 0 &-cos(\pi/4) &sin(\pi/4) \\ -sin(\pi/3) &sin(\pi/4) \cdot cos(\pi/3) &cos(\pi/3) \cdot cos(\pi/4) \end{bmatrix} Rposeg=−cos(π/3)0−sin(π/3)−sin(π/3)⋅sin(π/4)−cos(π/4)sin(π/4)⋅cos(π/3)−cos(π/4)⋅sin(π/3)sin(π/4)cos(π/3)⋅cos(π/4)
为了使用Pinocchio计算(δu\delta_uδu),需要使用以下代码将(RposesR_{pose_s}Rposes)和(RposegR_{pose_g}Rposeg)矩阵转换为四元数:
float s = 0.5f / sqrtf(trace+ 1.0f);
q.x = ( R[2][1] - R[1][2] ) * s;
q.y = ( R[0][2] - R[2][0] ) * s;
q.z = ( R[1][0] - R[0][1] ) * s;
q.w = 0.25f / s;
四元数的分量为:
- 对于第一次旋转
0.69352
-0.13795
0.13795
0.69352
- 对于第二次旋转
0.191342
-0.46194
0.331414
0.800103
现在每个位姿都有一个由七个分量组成的数学对象,并且都进行了归一化。与(SE(2)SE(2)SE(2))的例子一样,我们使用以下代码计算(δu\delta_uδu):
pose_s(0) = 1.0; pose_s(1) = 1.0;
pose_s(2) = 1 ; pose_s(3) = -0.13795 ;
pose_s(4) = 0.13795; pose_s(5) = 0.69352; pose_s(6) = 0.69352;
pose_g(0) = 4; pose_g(1) = 3 ;
pose_g(2) = 3 ; pose_g(3) = -0.46194;
pose_g(4) = 0.331414; pose_g(5) = 0.800103; pose_g(6) = 0.191342;
aSE3.difference(pose_s,pose_g,delta_u);
std::cout << delta_u << std::endl;
差异存在于(SE(3)SE(3)SE(3))的切空间中,由一个六维实向量表示:
-1.50984
-3.58755
2.09496
-0.374715
0.887794
0.86792
前三个值是线性部分,后三个值是角速度部分。
为了验证这是正确的结果,我们进行积分:
SpecialEuclideanOperationTpl<3,Scalar,Options>::ConfigVector_t pose_check;
aSE3.integrate(pose_s,delta_u,pose_check);
std::cout << pose_check << std::endl;
确实,我们得到:
4
3
3
-0.46194
0.331414
0.800103
0.191234
使用插值绘制轨迹
假设我们希望机器人经过已知位置,可以使用插值来绘制轨迹。
问题在于,像拉格朗日插值这样的方法只考虑平移,而机器人与环境的交互涉及平移和旋转。
一种可行的方法是使用基于四元数的(δθ\delta_{\theta}δθ)方法。该方法很简单,只需以非常小的变化量改变四元数的标量部分(即角度)。
以之前的例子为例,我们可以使用以下代码进行轨迹插值:
SpecialEuclideanOperationTpl<3,Scalar,Options>::ConfigVector_t pole;
aSE3.interpolate(pose_s,pose_g,0.5f, pole);
std::cout << pole << std::endl;
输出对应于轨迹的中间位置:
2.7486
1.4025
2.22461
-0.316431
0.247581
0.787859
0.466748
运动学算法
正向运动学
Pinocchio实现了直至二阶的直接运动学计算。给定机器人的配置,会执行正向传递,计算每个关节的空间位置,并将其存储为坐标变换。如果给定速度,它还会计算每个关节的空间速度(在局部坐标系中表示),加速度的计算也是如此。
运动学雅可比矩阵
每个关节的空间雅可比矩阵可以通过一次正向传递轻松计算出来,可以在局部坐标系或世界坐标系中表示。
动力学算法
逆动力学
递归牛顿 - 欧拉算法(RNEA)用于计算逆动力学:给定期望的机器人配置、速度和加速度,计算并存储执行该运动所需的扭矩。该算法首先执行正向传递(等同于二阶运动学计算),然后执行反向传递,计算沿结构传递的力螺旋,并提取获得计算出的连杆运动所需的关节扭矩。通过适当的输入,该算法还可用于计算动力学模型的特定项,如重力效应。
关节空间惯性矩阵
复合刚体算法(CRBA)用于计算机器人的关节空间惯性矩阵。我们对原始算法进行了一些细微修改,提高了计算效率。
正向动力学
铰接体算法(ABA)用于计算无约束正向动力学:给定机器人的配置、速度、扭矩和外力,计算出由此产生的关节加速度。
其他算法
除了上述算法外,还提供了其他方法,最显著的是用于约束正向动力学、冲量动力学、关节空间惯性矩阵求逆以及质心动力学的算法。
操作框架
待办事项:由于框架对于理解前面的章节并非必要内容,将其单独处理可能是个不错的主意。在此处引入框架相关内容以及相关算法。
解析导数
除了提供标准的正向和逆动力学算法,Pinocchio还高效地实现了它们的解析导数。这些导数在诸如全身轨迹优化,或者更广泛的数值最优控制等场景中至关重要。据我们所知,Pinocchio是首个原生实现这一特性的刚体框架。
自动微分与源代码生成
除了解析导数,Pinocchio还支持自动微分。这得益于整个C++代码的完全“标量”模板化,以及使用像ADOL-C、CasADi、CppAD等自动微分外部库。需要注意的是,这些自动求导的速度通常比解析求导慢很多。
Pinocchio另一个独特且核心的特性是它能够在编译时和运行时生成代码。这是通过另一个名为CppADCodeGen的外部工具实现的,该工具基于CppAD构建。对于任何使用Pinocchio的函数,CppADCodeGen都能够即时生成多种语言的代码,如C、Latex等,并且还能对数学表达式进行简化。借助这一过程,可以生成针对特定机器人模型的代码,并在Pinocchio外部使用。
Python绑定
待办事项:……
单元测试
待办事项:……




















 5063
5063

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








