
数学公式
本节介绍皮诺曹(Pinocchio)所使用的数学公式,它是费瑟斯通(Featherstone)算法的基础。
刚体 rigid-bodies.md
几何
刚体系统是由不同部分组成的集合,这些部分包括关节、刚体和力。一个关节连接两个不同的物体,并整合这两个物体之间的所有运动学关系,使得两个物体之间能够产生相对位移。这种位移可分解为三个部分来描述:旋转、平移或者旋转与平移的组合。
旋转矩阵构成了所谓的特殊正交群 SO(n)
。目前我们感兴趣的是其中的两个群:SO(2)
和 SO(3)
。SO(3)
是三维空间中所有旋转的群。它的元素是3×3大小的矩阵。SO(2)
对平面问题很有用。它是二维空间中的旋转群。它的元素是2×2大小的矩阵。
所有齐次变换矩阵组成的集合是特殊欧几里得群 SE(n)
。与旋转矩阵类似,也有两个不同的群,SE(3)
用于三维变换,SE(2)
用于二维变换,即在平面内的变换。
对 SO(3)
对象使用四元数
要对 SO(3)
对象使用四元数,我们有几种方法。我们可以像在 [处理李群几何](@ref md_doc_a - features_e - lie) 部分的 SE(3)
示例中那样,去掉平移向量。
或者我们可以只考虑一次旋转而不是两次。例如,在与机器人自身相关的一个地标链接中,我们将起始位置视为这个地标的原点。
那么让我们考虑三维空间中的一个立方体。

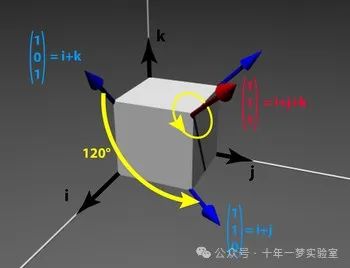

使用四元数的好处
确定与旋转对应的矩阵并非易事,所以很多时候物理问题是由对

来定义的。与旋转组合相关的另一个问题被称为 “万向节锁”:我们可以在特定情况下看到它,例如当两个连续的关节具有相近甚至对齐的旋转轴时。在这种情况下,第一个角度的很大变化不会改变设备末端的位置。由于计算的近似性,机器人可能会在不知不觉中产生非常强烈的剧烈运动。为了解决这两个问题,我们使用四元数。
笛卡尔积
当然,笛卡尔积对于分析和描述我们欧几里得空间中的运动至关重要。但这里,它是特定于李代数的,这与定义我们空间的笛卡尔积不同。
笛卡尔积也可用于通过关联与李代数相关的空间(如 SE(n)
和 SO(n)
群)来创建一个特定空间。
例如,让我们考虑像Tiago这样的轮式机器人。它只能在地面上移动。可以将地面看作一个平面。机器人可以绕z轴旋转,所以我们要处理一个 SE(2)
对象。然后我们给这个 SE(2)
对象连接一个有四个旋转关节的机械臂来伸展它的手臂,每个关节都有一个旋转自由度,所以它们是 SO(2)
对象。为了处理这个集合,我们使用与李代数相关的笛卡尔积,从而得到一个新的空间,在这个空间中我们能够表示机器人及其手臂所有可能的轨迹。
向量空间
如果你想创建一个切空间来简化轨迹的计算,就需要使用向量空间。实际上,切空间是一个向量空间,它是所有速度向量的集合。
让我们考虑一个有轨迹的物体,它的所有点都有一个与轨迹相切的速度,与一个速度相关且经过轨迹上某一点的空间就是切空间。
此外,通过使用向量空间,我们有可能利用它的性质,比如欧几里得叉乘算子和线性组合的性质。
然而,重要的是要知道这里的 “向量空间” 与李代数相关,这与我们通常处理的向量空间是不同的。
运动学
动力学
关节动力学 joints dynamics
几何
关节并非简单的物体,处理起来可能颇具难度。为便于对其进行描述,Pinocchio 使用了李代数,这在《处理李群几何》章节中有阐述。下面我们以基础关节为例,用李代数来表示它们:


构型空间 Configuration Space
运动学
运动链是一种数学模型,它能够根据施加到每个关节的旋转(可能还有平移),计算出由机器人连续关节连接的所有元件的位置,特别是末端元件的位姿。计算从初始元件的位姿开始,逐步进行。除了连续计算过程中的任何舍入误差外,最终元件的位姿在数学上是唯一且完全确定的。
在实际中,问题则大不相同。我们知道初始元件的位姿(例如机器人底座),并且我们希望设定其某个元件(通常是末端元件)的位姿,比如机器人手臂末端夹具的位姿。一般情况下,有多种关节旋转组合都能得到相同的最终位姿。通过观察我们的手可以在不同的肩部和手腕旋转组合下,以相同的姿势握住杯子,就可以很容易验证这一点。
逆运动学(通常缩写为 IK)指的是所有为了获得期望位姿而计算位置和旋转的方法。由于该问题可能存在多种解决方案,因此必须使用优化技术。机器人技术中使用的逆运动学方法可以考虑机器人的技术数据,例如通过保持机器人重心的位置,或者防止机器人倾倒。
最后需要注意的是,即使只有一种方法可以获得最终位姿,旋转也可以按不同顺序进行,并且每种情况下末端元件的轨迹都会不同。
在下图所示的情况下,存在大量可能性,手臂可能做出弯曲或直线轨迹,旋转可能在平移之前或之后进行等等。
TODO:添加 Pyrene 的动态图片
切空间
关节列表
关节是机器人在其环境中移动的关键组件。从某种程度上说,关节就如同机器人的关节部位。关节有多种类型,每种都由其形状和自由度来表征:
旋转关节
棱柱关节
圆柱关节
球关节
平移关节
自由浮动关节
此外,我们可以通过相互组合这些关节来创建更复杂的关节,称为复合关节。
旋转关节
我们要处理的最简单的旋转关节就是旋转关节,它只有一个自由度,因此我们可以专注于这一点。我们可以找到三种不同类型的旋转关节,每种类型可以围绕三个轴(x 轴、y 轴或 z 轴)中的一个进行旋转。旋转关节用于描述旋转运动。

棱柱关节
这同样是一个自由度为一的关节,但这次不再是旋转。通过棱柱关节,我们能够描述平移运动。与旋转关节类似,我们可以设置三种不同的棱柱关节,每种沿着一个轴(x 轴、y 轴或 z 轴)运动。

圆柱关节
圆柱关节有两个自由度,一个用于旋转,另一个用于平移。

球关节
球关节与人类关节最为相似,例如它和我们的髋关节很接近,但即使我们的身体有所限制,也无法围绕三个轴中的任何一个进行完整的转动。这个关节几乎相同,只是它可以围绕自身进行完整的旋转。所以这个关节可以围绕三个轴运动。它使机器人能够像我们一样移动其部件,甚至表现更好。

平面关节
顾名思义,平面关节允许物体在平面内进行运动。实际上,它允许两种平移和一种旋转,因此它有三个自由度。我们在日常生活中随处可见这种运动类型,汽车的运动就是如此,当我们在平坦的地面上行走时大多也是这种运动,例如这正是 Tiago(机器人)的运动方式。

平面关节的构型向量是四维的,坐标为 (x,y,cosθ,sinθ)
,代表相应的仿射变换矩阵:

平移关节
这种关节与球关节互补,它使得物体能够在三维空间中移动,但仅通过平移。这是一个自由度为三的关节。为了将其与我们的身体联系起来,我们可以想象固定脚踝关节以防止旋转,然后通过抬起和放下、上下、左右以及前后移动我们的脚。这正是平移关节所允许的运动。
自由浮动关节
这个关节允许在三维空间中进行具有六个自由度的自由运动。由于它所带来的多种可能性,它也是最难控制的非复合关节。
速查表:SE(3) 运算
刚体变换

复合变换
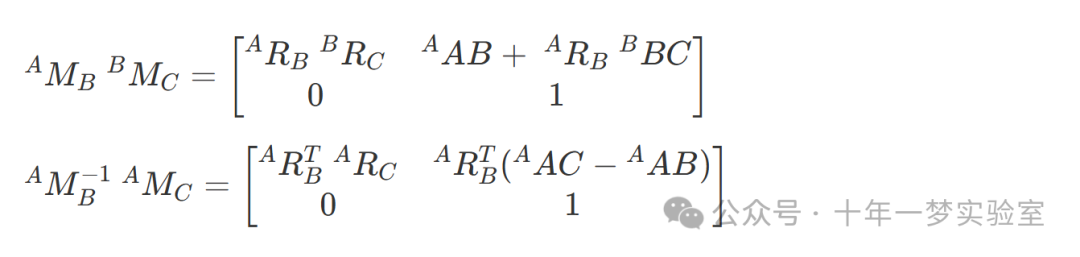
运动应用

力的应用

惯性
惯性应用

惯性相加
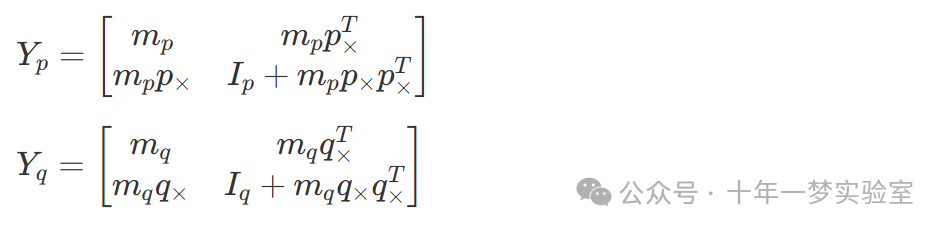
叉积
运动 - 运动叉积
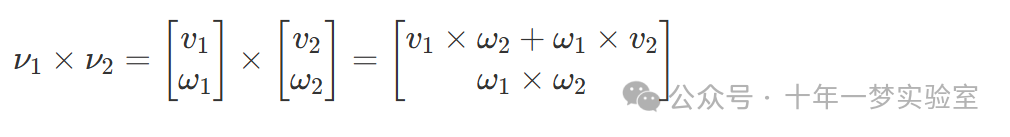
运动 - 力叉积

关节

递归牛顿 - 欧拉算法(RNEA)
初始化

前向循环

后向循环

注意

https://gepettoweb.laas.fr/doc/stack-of-tasks/pinocchio/master/doxygen-html/md_doc_c_maths_se3.html




















 1620
1620

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








