【Eigen教程】几何变换（七）

最新推荐文章于 2025-02-21 16:13:44 发布

十年一梦实验室

最新推荐文章于 2025-02-21 16:13:44 发布

阅读量1k

点赞数 17

本文链接：https://blog.youkuaiyun.com/cxyhjl/article/details/145485085

版权

1. 欧拉角

1.1. 介绍

欧拉角是描述刚体相对于固定坐标系的方向的三个角度。旋转可以围绕原始坐标系的轴 x-y-z（假设保持静止，外在的），或围绕旋转坐标系的轴 x-y-z（内在的，与运动的物体固连），每次基本旋转后相对于外在坐标系改变其方向。

1.2. 横滚、俯仰和偏航

欧拉角通常表示为：

γ 或 φ，表示绕 x 轴的旋转
β 或 θ，表示绕 y 轴的旋转
α 或 ψ，表示绕 z 轴的旋转

1.3. 正规欧拉角和泰特-布莱恩角

存在十二种可能的旋转轴序列，可以分为两类：

正规欧拉角，其中一个旋转轴重复（x-z-x, x-y-x, y-x-y, y-z-y, z-y-z, z-x-z）
泰特-布莱恩角，围绕所有轴旋转（x-z-y, x-y-z, y-x-z, y-z-x, z-x-y, z-y-x）

有时，这两类序列都称为“欧拉角”。在这种情况下，第一组的序列称为正规或经典欧拉角。对于泰特-布莱恩角，有六种选择旋转轴的可能性。六种可能的序列是：

x-y'-z'（内在旋转）或 z-y-x（外在旋转）
y-z'-x'（内在旋转）或 x-z-y（外在旋转）
z-x'-y'（内在旋转）或 y-x-z（外在旋转）
x-z'-y'（内在旋转）或 y-z-x（外在旋转）
z-y'-x'（内在旋转）或 x-y-z（外在旋转）：内在旋转称为：偏航、俯仰和横滚
y-x'-z'（内在旋转）或 z-x-y（外在旋转）

1.4 旋转矩阵

1.5 从旋转矩阵确定偏航、俯仰和滚转

有四个象限可供选择反正切函数。每个象限应通过使用参数的分子和分母的符号来选择。分子的符号选择方向是在x轴的上方还是下方，分母选择方向是在y轴的左侧还是右侧。函数atan2可以为我们计算：

1.6 符号和范围

1.7 泰特-布莱恩角

1.8 等效的正欧拉角

点击此处查看互动演示:
https://www.andre-gaschler.com/rotationconverter/

1.9. 旋转和平移在变换中的顺序

为了应用变换，首先我们在预乘的框架轴上应用旋转，然后我们在预乘的框架轴上再次平移

1.10. 万向节锁

角度 α、β 和 γ 是唯一确定的，除了奇异情况。如果 cos(β) = 0 或 β = ±π/2

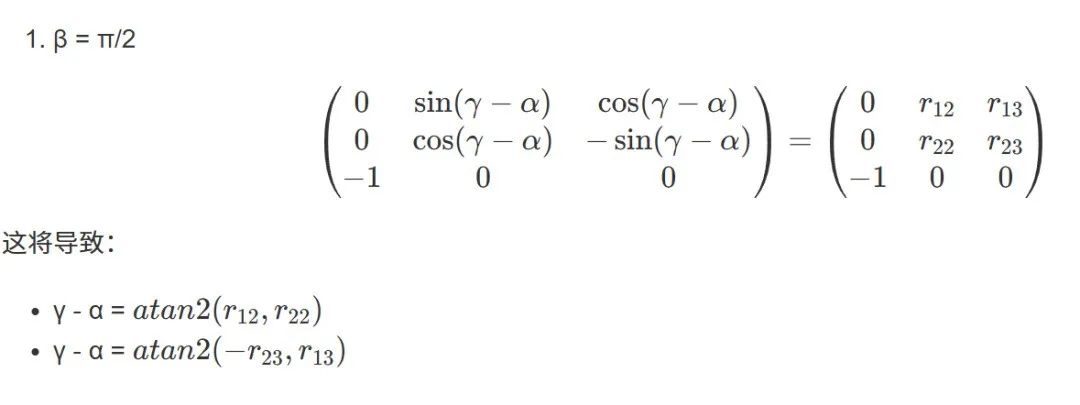
这意味着对于给定的旋转矩阵，在 β = ±π/2 时，有无限多组（滚动，偏航）角度。

访问链接：[link](https://compsci290-s2016.github.io/CoursePage/Materials/EulerAnglesViz/) ，查看交互式万向节可视化内容。

当然，让我们使用一个数值例子来说明万向节锁问题，然后解释该问题如何在欧拉角表示中表现出来，而不是四元数。

数值示例：

考虑一个我们希望使用滚-俯仰-偏航序列（通常在航空中使用）旋转的3D对象。为了简单起见，我们使用度数：

初始方向：未应用旋转。欧拉角为（滚动，俯仰，偏航）=（0°，0°，0°）。
旋转：我们应用+90°的俯仰。现在，我们的欧拉角为（0°，90°，0°）。

此时，对象的“鼻子”指向正上方。问题是：

如果我们现在尝试应用一个例如+45°的滚动，实际在3D空间中的效果将与应用+45°的偏航相同。我们无法区分滚动和偏航；它们已经退化。这就是万向节锁。

数值值：

欧拉角：

在+90°俯仰之后，我们的欧拉角变为：

滚动：0°（或+45°如果在俯仰后尝试滚动）
俯仰：90°
偏航：0°（或+45°如果在俯仰后尝试偏航）

这是有问题的，因为在+90°俯仰之后，滚动和偏航旋转在效果上是无法区分的。

四元数表示：

围绕Y轴的+90°俯仰旋转可以表示为：

现在，如果我们想在这个俯仰之后应用+45°的滚动，使用四元数，我们将上述四元数乘以围绕X轴的+45°滚动的四元数表示，结果是一个独特且唯一的四元数值，平滑地结合了这两个旋转而没有歧义。

为什么欧拉角有这个问题：

欧拉角的万向节锁问题的核心在于旋转的顺序性。当俯仰角为±90°时，滚动和偏航轴变得对齐。因此，围绕其中一个轴旋转与围绕另一个轴旋转是无法区分的。这种重叠或“锁定”导致了自由度的丧失。

为什么四元数没有这个问题：

四元数表示旋转为一个单一的、统一的操作，而不是一个序列。这意味着没有固有的顺序或序列需要担心。+90°俯仰旋转后的四元数旋转加上+45°滚动将产生一个独特的方向，与任何其他旋转组合不同。

此外，四元数在方向之间平滑插值（使用“球面线性插值”），确保连续的旋转而没有欧拉角相关的跳跃或奇点。

总之，四元数的非顺序性质，加上它们独特地表示每个可能方向的能力，使得它们避免了困扰欧拉角的万向节锁问题。

点击此处查看互动演示:
https://quaternions.online/

1.10. 3D旋转矩阵的唯一性

参考文献：matrices - $3D$ rotation matrix uniqueness - Mathematics Stack Exchange https://math.stackexchange.com/questions/105264/3d-rotation-matrix-uniqueness/105380#105380

2. 全局参考和局部切平面坐标

在选择移动和固定轴时，有几种轴约定，这些约定决定了角度的符号。

Tait-Bryan角通常用于描述车辆相对于选定参考系的姿态。车辆中的正x轴总是指向运动方向。对于正y轴和z轴，我们必须面对两种不同的约定：

2.1 东、北、上（ENU） East, North, Up

东、北、上（ENU），用于地理学（z轴向上，x轴在运动方向，y轴指向左）

2.2 北、东、下（NED）North, East, Down

北、东、下（NED），特别用于航空航天（z轴向下，x轴在运动方向，y轴指向右）

对于像汽车、坦克这样的陆地车辆，ENU系统（东-北-上）作为外部参考（世界坐标系），车辆（车体）的正y轴或俯仰轴总是指向其左侧，正z轴或偏航轴总是指向上。

对于像潜艇、船只、飞机等的空中和海上车辆，使用NED系统（北-东-下）作为外部参考（世界坐标系），车辆（车体）的正y轴或俯仰轴总是指向其右侧，正z轴或偏航轴总是指向下。

数学公式：

3. 轴角表示

轴角表示在三维欧几里得空间中的旋转由两个量表示：

一个单位向量 e 表示旋转轴的方向，
一个角度 θ

示例：

上述例子可以表示为：

罗德里格斯旋转公式

旋转的指数坐标

泰勒级数

刚体运动的指数坐标

4. 四元数

四元数数系扩展了由威廉·罗恩·哈密顿引入的复数。哈密顿将四元数定义为两个向量（在三维空间中的两条线）的商。四元数通常表示为以下形式：

其中 a, b, c 和 d 是实数；i, j 和 k 是基本四元数（可以解释为沿三个空间轴指向的单位向量的符号）。

4.1. 基础

四元数集合通过分量加法构成了实数上的四维向量空间，基为 {1,i,j,k}
，其乘法规则为：

四元数的向量定义：

4.1.1. 四元数惯例：哈密顿和JPL

参考文献：1
(https://fzheng.me/2017/11/12/quaternion_conventions_en/)

4.2. 四元数的逆

共轭

四元数的共轭是将虚部取相反数：

如果四元数与其共轭相乘，我们得到一个实数。实部是其长度的平方：

长度

四元数的长度定义为

可以验证，乘积的长度是长度的乘积。

四元数的逆为：

4.3. 四元数乘法（哈密顿积）

4.4 作为方向表示的四元数

4.5 用单位四元数变换参考坐标系

4.6 四元数逆位姿

4.7 四元数相对位姿

4.8 四元数与欧拉角之间的转换

有一篇关于四元数的非常不错的文章可供阅读。
https://danceswithcode.net/engineeringnotes/quaternions/quaternions.html

4.9 表示从一个向量到另一个向量旋转的四元数

参考文献：math - Finding quaternion representing the rotation from one vector to another - Stack Overflow https://stackoverflow.com/questions/1171849/finding-quaternion-representing-the-rotation-from-one-vector-to-another

4.10 四元数与轴 - 角表示

// P  = [0, p1, p2, p3]  <-- 点向量 P = [0, p1, p2, p3]
// alpha = 旋转角度
// [x, y, z] = 旋转轴（单位向量）
// R = [cos(alpha/2), sin(alpha/2)*x, sin(alpha/2)*y, sin(alpha/2)*z] <-- 旋转
// R' = [w, -x, -y, -z]
// P' = RPR'
// P' = H(H(R, P), R')

Eigen::Vector3d p(1,0,0);// 定义向量 p，初始值为 (1, 0, 0)

Quaternion P;// 定义四元数 P
P.w =0;// 四元数 P 的实部为 0
P.x =p(0);// 四元数 P 的 x 分量为向量 p 的第一个分量
P.y =p(1);// 四元数 P 的 y 分量为向量 p 的第二个分量
P.z =p(2);// 四元数 P 的 z 分量为向量 p 的第三个分量

// 旋转 90 度绕 y 轴
double alpha = M_PI /2;// 定义旋转角度 alpha 为 π/2（即 90 度）
Quaternion R;// 定义四元数 R
Eigen::Vector3d r(0,1,0);// 定义旋转轴向量 r，为 (0, 1, 0)
r = r.normalized();// 将旋转轴向量标准化

R.w =cos(alpha /2);// 四元数 R 的实部为 cos(alpha/2)
R.x =sin(alpha /2)*r(0);// 四元数 R 的 x 分量为 sin(alpha/2) * r 的第一个分量
R.y =sin(alpha /2)*r(1);// 四元数 R 的 y 分量为 sin(alpha/2) * r 的第二个分量
R.z =sin(alpha /2)*r(2);// 四元数 R 的 z 分量为 sin(alpha/2) * r 的第三个分量

std::cout << R.w <<","<< R.x <<","<< R.y <<","<< R.z << std::endl;// 输出四元数 R 的各分量

Quaternion R_prime =quaternionInversion(R);// 计算四元数 R 的共轭四元数 R'
Quaternion P_prime =quaternionMultiplication(quaternionMultiplication(R, P), R_prime);// 计算 P' = RPR'

// 旋转 90 度绕 y 轴后的点 (1, 0, 0)，结果是 (0, 0, -1)。
// 请注意，P' 的第一个元素总是 0，因此可以忽略。

参考: 1 rotations - How do you rotate a vector by a unit quaternion? - Mathematics Stack Exchange https://math.stackexchange.com/questions/40164/how-do-you-rotate-a-vector-by-a-unit-quaternion

4.11 用四元数完整表示一个坐标系

为了在三维空间中表示一个位置，使用表示方向的四元数和表示位置的向量的组合。

对于位置，可以使用 Vector3d，它是一个由三个双精度数组成的向量。
对于方向，使用 Quaterniond，它是一个使用双精度的四元数。

定义位置和方向

Eigen::Vector3d position(1.0, 2.0, 3.0); // 示例位置 (x, y, z)
Eigen::Quaterniond orientation; // 用于方向的四元数

初始化四元数

可以通过几种方式初始化四元数，例如从轴 - 角表示、从旋转矩阵或直接设置其分量。

// 示例：从轴和角度初始化四元数
Eigen::Vector3d axis(0, 1, 0); // 围绕 y 轴旋转
double angle = M_PI / 4; // 45 度
orientation = Eigen::AngleAxisd(angle, axis.normalized());

使用位置和方向

一旦有了位置和四元数，就可以用它们来变换点、计算旋转等。

// 示例：使用四元数旋转一个点
Eigen::Vector3d point(1, 0, 0);
Eigen::Vector3d rotatedPoint = orientation * point;

组合位置和方向

如果你想创建一个同时包含位置和方向的变换矩阵，可以使用仿射变换。

Eigen::Affine3d transform = Eigen::Translation3d(position) * orientation;

4.12 用四元数表示的坐标系的乘法

下面是一个完整的综合示例：

double x1 =1.0, y1 =0.0, z1 =0.0;
// 定义变量 x1, y1, z1 表示第一个位置的坐标
double q_w1 =1.0, q_x1 =0.0, q_y1 =0.0, q_z1 =0.0;
// 定义四元数 q_w1, q_x1, q_y1, q_z1 表示第一个姿态的四元数
double x2 =1.0, y2 =0.0, z2 =0.0;
// 定义变量 x2, y2, z2 表示第二个位置的坐标
double q_w2 =1.0, q_x2 =0.0, q_y2 =0.0, q_z2 =0.0;
// 定义四元数 q_w2, q_x2, q_y2, q_z2 表示第二个姿态的四元数

Eigen::Affine3d pose1 =Eigen::Translation3d(x1, y1, z1)*Eigen::Quaterniond(q_w1, q_x1, q_y1, q_z1);
// 创建第一个变换矩阵 pose1，结合了位移和四元数表示的旋转
Eigen::Affine3d pose2 =Eigen::Translation3d(x2, y2, z2)*Eigen::Quaterniond(q_w2, q_x2, q_y2, q_z2);
// 创建第二个变换矩阵 pose2，结合了位移和四元数表示的旋转

Eigen::Affine3d result = pose1 * pose2;
// 计算 pose1 和 pose2 的复合变换，并将结果存储在 result 中

Eigen::Vector3d res_translation = result.translation();
// 提取 result 变换中的平移部分
Eigen::Quaterniond res_quaternion(result.rotation());
// 提取 result 变换中的旋转部分，并将其表示为四元数

std::cout <<"Resulting Pose Translation: "<< res_translation.transpose()<< std::endl;
// 输出复合变换的平移部分
std::cout <<"Resulting Pose Quaternion: "
          << res_quaternion.w()<<" "
          << res_quaternion.x()<<" "
          << res_quaternion.y()<<" "
          << res_quaternion.z()<< std::endl;
// 输出复合变换的四元数部分

这段代码先定义了两个位置和对应的姿态四元数，然后创建结合了位移和平移的变换矩阵 pose1 和 pose2，计算它们的复合变换，并提取平移和旋转部分，最后输出复合变换的平移和四元数表示。

使用四元数进行旋转：

使用轴 - 角进行旋转：

4.12.1 使用四元数旋转向量

4.12.2 用四元数变换位置的完整表示（方向和位移）

当你拥有一个同时包含方向（旋转）和位移的位置完整表示，并且想要使用四元数对其进行变换时，你需要同时考虑旋转和位移分量。

我们进行如下表示：

为了用变换坐标系对源坐标系进行变换：

使用变换坐标系的方向来旋转源坐标系的方向。
用变换坐标系的方向来旋转源坐标系的位移，然后加上变换坐标系的位移。

以下是一个使用 `numpy` 和 `numpy - quaternion` 库的 Python 代码示例：

import numpy as np
import quaternion

# 定义四元数和位移
# 为了示例的目的，假设如下：
# 对于两个坐标系，分别绕 z 轴旋转 45 度
# 并且平移 (1,0,0)

angle = np.pi /4
# 定义旋转角度为 45 度 (π/4)

axis = np.array([0,0,1])
# 定义旋转轴为 z 轴

q_s = quaternion.from_rotation_vector(angle * axis)
# 将旋转角度和轴转换为四元数 q_s 表示源坐标系的旋转

t_s = np.array([1,0,0])
# 定义源坐标系的平移向量 t_s

q_t = quaternion.from_rotation_vector(angle * axis)
# 将旋转角度和轴转换为四元数 q_t 表示目标坐标系的旋转

t_t = np.array([1,0,0])
# 定义目标坐标系的平移向量 t_t

# 1. 复合旋转
q_combined = q_t * q_s
# 计算两个旋转的复合四元数 q_combined

# 2. 旋转源坐标系的平移向量，然后进行平移
# 将平移向量转换为四元数形式
t_s_quat = np.quaternion(0, t_s[0], t_s[1], t_s[2])

# 旋转平移向量
t_s_rotated_quat = q_t * t_s_quat * q_t.inverse()

# 提取旋转后的向量部分并加上目标坐标系的平移
t_combined = np.array([t_s_rotated_quat.x, t_s_rotated_quat.y, t_s_rotated_quat.z])+ t_t

print(f"Combined Orientation (Quaternion): {q_combined}")
# 输出复合旋转的四元数表示

print(f"Combined Translation: {t_combined}")
# 输出复合平移向量

这段代码首先定义了两个四元数和对应的位移向量，然后计算两个旋转的复合四元数，并旋转源坐标系的平移向量，再将结果加上目标坐标系的平移，最后输出复合的旋转（四元数表示）和平移向量。

4.12.3 用四元数表示的完整位姿（位置和方向）的逆

4.12.4 两个相机与惯性测量单元（IMU）相对位姿示例

如果给定的变换是惯性测量单元在相机坐标系中的位置，那么我们需要对方法稍作修改。

我们用Python实现这一过程：

import numpy as np
from pyquaternion import Quaternion

defrelative_pose(q_C0_IMU, t_C0_IMU, q_C1_IMU, t_C1_IMU):
    # 计算相对四元数
    q_C0_C1 = q_C0_IMU * q_C1_IMU.inverse

    # 计算相对位移
    t_diff = np.array(t_C1_IMU)- np.array(t_C0_IMU)
    t_C0_C1 = q_C0_IMU.rotate(t_diff)

    return q_C0_C1, t_C0_C1.tolist()

# 定义 IMU 相对于 Camera0 和 Camera1 的四元数和位移
q_C0_IMU = Quaternion(w=0.6328142, x=0.3155095, y=-0.3155095, z=0.6328142)
t_C0_IMU =[0.234508,0.028785,0.039920]

q_C1_IMU = Quaternion(w=0.3155095, x=-0.6328142, y=-0.6328142, z=-0.3155095)
t_C1_IMU =[0.234508,0.028785,-0.012908]

q_C0_C1, t_C0_C1 = relative_pose(q_C0_IMU, t_C0_IMU, q_C1_IMU, t_C1_IMU)
print("相对于 Camera0 的 Camera1 四元数:", q_C0_C1)
print("相对于 Camera0 的 Camera1 位移:", t_C0_C1)

这段代码首先定义了 IMU 相对于 Camera0 和 Camera1 的四元数和位移，然后计算它们之间的相对姿态（四元数表示）和相对位移。最后输出相对姿态和位移的结果。
这段 Python 代码应该能得出相机1相对于相机0的位姿。

4.12.5 用四元数表示相对位姿（下标消去法）

4.13 四元数球面线性插值（Slerp）

下面是使用 C++ 和 Eigen 库实现四元数球面线性插值（Slerp）的代码示例：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>

// 定义一个函数来进行四元数球面线性插值（Slerp）
Eigen::Quaterniond slerp(const Eigen::Quaterniond& q1,const Eigen::Quaterniond& q2,double t){
    // 计算两个四元数之间的夹角
    double dot_product = q1.dot(q2);
    
    // 如果点积小于 0，取反以获得最短路径插值
    if(dot_product <0.0){
        q2 =-q2;
        dot_product =-dot_product;
    }
    
    // 限制点积在 [0, 1] 之间
    dot_product = std::clamp(dot_product,-1.0,1.0);
    
    // 计算夹角 theta
    double theta = std::acos(dot_product);
    
    // 计算插值权重
    double sin_theta = std::sqrt(1.0- dot_product * dot_product);
    
    // 如果 sin(theta) 非常小（接近 0），直接返回线性插值
    if(std::abs(sin_theta)<1e-6){
        returnEigen::Quaterniond(
            (1.0- t)* q1.coeffs()+ t * q2.coeffs()
        ).normalized();
    }
    
    // 使用 Slerp 公式计算插值四元数
    double a = std::sin((1.0- t)* theta)/ sin_theta;
    double b = std::sin(t * theta)/ sin_theta;
    return(a * q1.coeffs()+ b * q2.coeffs()).normalized();
}

intmain(){
    // 定义两个四元数
    Eigen::Quaterniond q1(0.7071,0.0,0.7071,0.0);// 四元数1
    Eigen::Quaterniond q2(0.0,0.7071,0.7071,0.0);// 四元数2
    
    // 进行插值
    double t =0.5;// 插值参数（0 <= t <= 1）
    Eigen::Quaterniond q_interp =slerp(q1, q2, t);
    
    // 输出结果
    std::cout <<"Interpolated Quaternion: "<< q_interp.coeffs().transpose()<< std::endl;
    
    return0;
}

这段代码定义了一个函数 slerp，用于计算两个四元数之间的球面线性插值，并在 main 函数中示例化了两个四元数，并计算它们在 t=0.5
位置的插值。最后输出插值结果。