【C++】sophus : ceres_typetraits.hpp、ceres_manifold.hpp (九)

ceres_typetraits.hpp

这段代码主要定义了用于区分和映射向量类型和标量类型的工具。下面是详细总结：

1. 命名空间和头文件保护：

• 使用预处理指令#ifndef 和#define 定义头文件保护，防止重复包含。

• 引入头文件common.hpp。

模板函数和类型特征：

• 定义了两个模板函数complete，用于检测类型 T 是否完整，并返回std::true_type 或std::false_type。

• 使用模板别名IsSpecialized 检测类型 T 是否特化。

区分可映射向量类型和标量类型的类型特征：

• 使用模板别名IsMappable 区分类型 T 是否可以映射到Eigen::Map。

• 定义一个constexpr 布尔值IsMappableV，用于表示类型 T 是否可映射。

Mapper 模板结构体：

• 定义了一个模板结构体Mapper，用于将标量或向量类型映射到指向数据的指针。

• Mapper 结构体根据不同的条件进行特化，处理标量类型和可映射类型。

• 对于标量类型，Mapper 直接返回标量引用。

• 对于可映射类型，Mapper 使用Eigen::Map 进行映射。

代码的实际应用：

• 该工具主要用于在LieGroup 库中，将不同的切向量类型（如标量或向量）映射到原始数据上，便于进行进一步的数学运算。

这段代码体现了模板编程和类型特征在现代 C++ 中的重要性，能够灵活处理不同类型的数据结构，保证代码的通用性和高效性。

#ifndef SOPHUS_CERES_TYPETRAITS_HPP#define SOPHUS_CERES_TYPETRAITS_HPP
#include "common.hpp"
namespace Sophus {
// 定义一个模板函数 complete，当传入的类型 T 存在并且可以取其大小时返回 std::true_type 类型template <class T, std::size_t = sizeof(T)>constexpr std::true_type complete(T*);// 定义另一个模板函数 complete，当传入的类型 T 不存在或无法取其大小时返回 std::false_type 类型constexpr std::false_type complete(...);
// 定义一个模板别名 IsSpecialized，用于检测类型 T 是否特化template <class T>using IsSpecialized = decltype(complete(std::declval<T*>()));
/// 用于区分可映射的向量类型和标量类型的类型特征////// 我们使用这个类来区分 LieGroup<T>::Tangent 中的 Sophus::Vector<Scalar, N> 和标量类型////// 主要用于将 LieGroup::Tangent 映射到原始数据，有两种选项：///  - LieGroup::Tangent 是 "scalar" (例如 SO2)，则直接解引用指针///  - LieGroup::Tangent 是 Sophus::Vector<...>，则需要使用 Eigen::Map////// 特化 Eigen::internal::traits<T> 对于构造 Eigen::Map<T> 至关重要，因此我们使用该属性来区分这两种选项。/// 目前似乎没有选项可以仅使用 Eigen 的 "external" API 进行检查。template <class T>using IsMappable = IsSpecialized<Eigen::internal::traits<std::decay_t<T>>>;
// 定义一个 constexpr 布尔值 IsMappableV，用于表示类型 T 是否可映射template <class T>constexpr bool IsMappableV = IsMappable<T>::value;
/// 辅助模板结构体，用于将切向量（标量）映射到指向数据的指针template <typename T, typename E = void>struct Mapper {  using Scalar = T;  using Map = Scalar&;  using ConstMap = const Scalar&;
  // 定义 map 函数，将标量指针映射到标量引用  static Map map(Scalar* ptr) noexcept { return *ptr; }  // 定义 map 函数，将 const 标量指针映射到 const 标量引用  static ConstMap map(const Scalar* ptr) noexcept { return *ptr; }};
// 特化的 Mapper 模板结构体，用于处理可映射类型template <typename T>struct Mapper<T, typename std::enable_if_t<IsMappableV<T>>> {  using Scalar = typename T::Scalar;  using Map = Eigen::Map<T>;  using ConstMap = Eigen::Map<const T>;
  // 定义 map 函数，将标量指针映射到 Eigen::Map<T>  static Map map(Scalar* ptr) noexcept { return Map(ptr); }  // 定义 map 函数，将 const 标量指针映射到 Eigen::Map<const T>  static ConstMap map(const Scalar* ptr) noexcept { return ConstMap(ptr); }};
}  // namespace Sophus
#endif

这段代码定义了一组工具，用于支持在 Sophus 中处理模板类型和 Lie 群切向量的映射。它主要通过类型特性（type traits）和模板元编程为 Sophus 库中的 Lie 群实现提供了灵活性和扩展性。以下是总结：

---

功能和用途

1. 类型特性检测：

• 提供一种机制来检查类型是否具有特定的内部特性（如 Eigen 的 internal::traits）。

• 使用这些特性区分可映射的向量类型和标量类型。

数据映射（Mapping）：

• 提供一个通用工具类 Mapper，用于将 Lie 群的切向量映射到原始数据指针。

• 根据类型不同，Mapper 处理标量（如 double）或向量（如 Eigen::Vector）的映射，适配不同 Lie 群切向量的需求。

---

主要组件

1. 类型检查工具

• IsSpecialized

  ：

  template <classT, std::size_t =sizeof(T)>constexpr std::true_typecomplete(T*);constexpr std::false_typecomplete(...);template <classT>using IsSpecialized =decltype(complete(std::declval<T*>()));

  • 利用 decltype 和 sizeof 检测类型是否定义了 Eigen::internal::traits。

  • 检查一个类型是否为特定模板的特化类型。

  • 实现方式：

• IsMappable 和 IsMappableV

  ：

  • 用于判断一个类型是否可以映射（是否为 Eigen 向量类型）。

  • IsMappable<T>

     检测类型 T 是否特化了 Eigen::internal::traits。

  • IsMappableV

     提供值版本，简化了调用。

2. 数据映射工具：Mapper

• 作用

  ：

  • 根据类型的特性（标量或向量），提供不同的映射方式。

  • 标量

    ：直接解引用指针。

  • 向量

    ：通过 Eigen::Map 实现映射。

• 实现细节

  ：

  • 默认模板处理标量类型：

    template <typename T,typename E =void>struct Mapper {using Scalar = T;using Map = Scalar&;using ConstMap =const Scalar&;static Mapmap(Scalar* ptr)noexcept{return *ptr; }static ConstMapmap(const Scalar* ptr)noexcept{return *ptr; } };

  • 对可映射向量类型（IsMappableV<T> == true）的特化：

    template <typename T>structMapper<T,typename std::enable_if_t<IsMappableV<T>>> {using Scalar =typename T::Scalar;using Map = Eigen::Map<T>;using ConstMap = Eigen::Map<const T>;static Mapmap(Scalar* ptr)noexcept{returnMap(ptr); }static ConstMapmap(const Scalar* ptr)noexcept{returnConstMap(ptr); } };

---

应用场景

1. Lie 群切向量的数据映射：

• 适配 Lie 群中切向量的存储和操作。

• 例如，在优化中使用切向量进行参数更新时，可以直接通过 Mapper 将指针映射为 Eigen 的 Map 类型。

类型区分：

• 在需要对标量和向量类型执行不同操作的场景中，IsMappable 提供了编译期的类型分类能力。

与 Eigen 和 Sophus 的集成：

• 通过检测 Eigen::internal::traits，实现对 Sophus 和 Eigen 类型的无缝支持。

---

主要优势

1. 泛型支持：

• 通过模板和类型特性，支持任意标量类型或可映射向量类型。

高效映射：

• 使用 Eigen::Map 避免了拷贝，实现了直接在原始数据上操作。

可扩展性：

• 提供了扩展 Lie 群类型和切向量映射的基础。

Sophus 和 Eigen 集成友好：

• 对 Eigen 的内部特性进行了深度利用，专门为 Eigen::Vector 提供支持。

---

示例用法

• 标量类型（如 double）

  ：

  double data =1.23;auto value = Sophus::Mapper<double>::map(&data);// 返回 data 的引用

• 向量类型（如 Eigen::Vector3d）

  ：

  Eigen::Vector3ddata(1.0,2.0,3.0);auto map = Sophus::Mapper<Eigen::Vector3d>::map(data.data());// 返回 Eigen::Map

---

---

ceres_manifold.hpp

这段代码定义了一个模板化的 Manifold 类，它是基于 Ceres 优化库中的 ceres::Manifold，用于处理 Sophus 中的 Lie 群操作。以下是代码的总结：

背景

Lie 群广泛用于机器人学、计算机视觉和图形学中的运动表示。Sophus 是一个 C++ 库，用于表示和操作 Lie 群及其相关的数学对象。

功能

Manifold 类实现了 Ceres 的流形接口，允许在优化中使用 Sophus 的 Lie 群表示。Ceres 的流形接口为优化问题提供了自定义的加法、减法和相关的雅可比计算。

主要功能概述

1. 模板化设计：

• 通过模板参数 LieGroup，支持不同维度或类型的 Lie 群（如 SE(3)、SO(3) 等）。

• LieGroup<double>

   定义了具体的 Lie 群实现，Tangent 是其对应的切空间类型。

核心接口实现：

• Plus: 定义 Lie 群上的“加法”操作（通过指数映射）。

  • • 数学公式：T_plus_delta = T * exp(delta)

    • exp(delta)

       将切空间增量 delta 映射到 Lie 群上。

• PlusJacobian: 计算“加法”操作在零增量 delta=0 时的雅可比矩阵。

  • 数学公式：Dx T * exp(x) | x=0

• Minus

  : 定义 Lie 群上的“减法”操作（通过对数映射）。

  • 数学公式：y_minus_x = log(x.inverse() * y)

  • 将 Lie 群元素 x 和 y 的差值映射到切空间。

• MinusJacobian

  : 计算“减法”操作的雅可比矩阵。

  • 数学公式：Dx log(x.inverse() * y) | x=0

• AmbientSize 和 TangentSize: 分别返回 Lie 群参数维度和切空间维度。

矩阵映射：

• 使用 Eigen 提供的 Map 和 Sophus 的 Mapper，方便在 C++ 数组和 Eigen 对象之间切换。

• 例如，TangentConstMap 和 TangentMap 直接映射到切空间。

扩展性：

• 通过模板参数和虚函数，支持各种 Lie 群的流形操作，可直接集成到 Ceres 优化问题中。

代码应用场景

• 用于非线性优化问题，其中变量位于 Lie 群（例如旋转 SO(3) 或刚体变换 SE(3)）上。

• 提供了一种无缝将 Sophus 和 Ceres 集成的方法，简化了 Lie 群相关问题的雅可比计算。

优点

• 模块化设计

  ：模板化和继承使得代码易于扩展到其他 Lie 群类型。

• 高效计算

  ：借助 Sophus 的预定义函数（如 exp、log、Dx_this_mul_exp_x_at_0），避免手动推导和实现雅可比。

• 优化友好

  ：符合 Ceres 的接口规范，能直接在 Ceres 中定义流形约束优化问题。

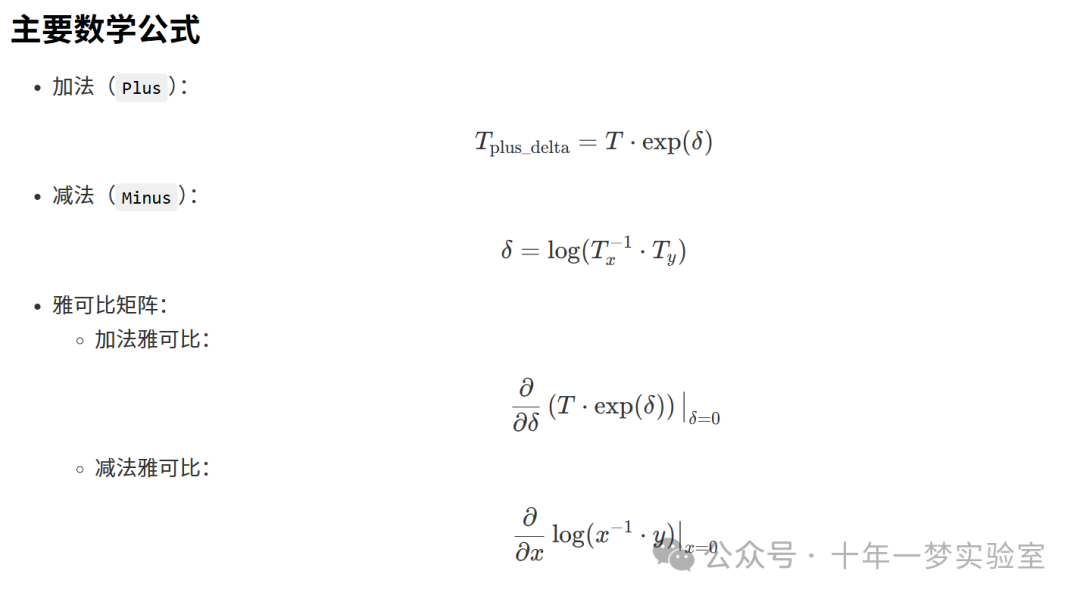
#pragma once
#include <ceres/manifold.h>  // 包含 Ceres 库中的流形头文件#include <sophus/ceres_typetraits.hpp>  // 包含 Sophus 库中的类型特征头文件
namespace Sophus {
/// 为 LieGroup 实现的模板化局部参数化（实现了 LieGroup::Dx_this_mul_exp_x_at_0() ）template <template <typename, int = 0> class LieGroup>class Manifold : public ceres::Manifold { public:  using LieGroupd = LieGroup<double>;  // 使用 double 类型实例化 LieGroup 模板  using Tangent = typename LieGroupd::Tangent;  // 定义切向量类型  using TangentMap = typename Sophus::Mapper<Tangent>::Map;  // 定义切向量的映射类型  using TangentConstMap = typename Sophus::Mapper<Tangent>::ConstMap;  // 定义常量切向量的映射类型  static int constexpr DoF = LieGroupd::DoF;  // 定义自由度常量  static int constexpr num_parameters = LieGroupd::num_parameters;  // 定义参数数量常量
  /// LieGroup 在 Ceres 中的加操作  ///  ///  T * exp(x)  ///  bool Plus(double const* T_raw, double const* delta_raw,            double* T_plus_delta_raw) const override {    Eigen::Map<LieGroupd const> const T(T_raw);  // 将原始数据映射为常量 LieGroupd    TangentConstMap delta = Sophus::Mapper<Tangent>::map(delta_raw);  // 将原始增量数据映射为常量切向量    Eigen::Map<LieGroupd> T_plus_delta(T_plus_delta_raw);  // 将结果数据映射为 LieGroupd    T_plus_delta = T * LieGroupd::exp(delta);  // 计算 T * exp(delta)    return true;  }
  /// LieGroup 在 Ceres 中的加操作的雅可比矩阵  ///  /// Dx T * exp(x)  当 x=0 时  ///  bool PlusJacobian(double const* T_raw, double* jacobian_raw) const override {    Eigen::Map<LieGroupd const> T(T_raw);  // 将原始数据映射为常量 LieGroupd    Eigen::Map<Eigen::Matrix<double, num_parameters, DoF,                             DoF == 1 ? Eigen::ColMajor : Eigen::RowMajor>>        jacobian(jacobian_raw);  // 将雅可比矩阵数据映射为矩阵类型    jacobian = T.Dx_this_mul_exp_x_at_0();  // 计算雅可比矩阵    return true;  }
  bool Minus(double const* y_raw, double const* x_raw,             double* y_minus_x_raw) const override {    Eigen::Map<LieGroupd const> y(y_raw), x(x_raw);  // 将原始数据映射为常量 LieGroupd    TangentMap y_minus_x = Sophus::Mapper<Tangent>::map(y_minus_x_raw);  // 将结果数据映射为切向量
    y_minus_x = (x.inverse() * y).log();  // 计算 x 的逆与 y 的乘积的对数    return true;  }
  bool MinusJacobian(double const* x_raw, double* jacobian_raw) const override {    Eigen::Map<LieGroupd const> x(x_raw);  // 将原始数据映射为常量 LieGroupd    Eigen::Map<Eigen::Matrix<double, DoF, num_parameters, Eigen::RowMajor>>        jacobian(jacobian_raw);  // 将雅可比矩阵数据映射为矩阵类型    jacobian = x.Dx_log_this_inv_by_x_at_this();  // 计算雅可比矩阵    return true;  }
  int AmbientSize() const override { return LieGroupd::num_parameters; }  // 返回参数数量
  int TangentSize() const override { return LieGroupd::DoF; }  // 返回自由度数量};
}  // namespace Sophus