广告插入:伯特兰盒子悖论——颠覆你的常识系列二。
相信大家都听过这样一个荒谬的说法: 1 + 2 + 3 + 4 + ⋯ = − 1 12 1+2+3+4+\dots=-\cfrac{1}{12} 1+2+3+4+⋯=−121,也就是所有的自然数之和等于一个定值,且是一个负数,这是咋证明出来的呢?让我们看这里:
首先我们需要知道几个式子:
-
1 − 1 + 1 − 1 + 1 − 1 + ⋯ = 1 2 1-1+1-1+1-1+\dots=\cfrac{1}{2} 1−1+1−1+1−1+⋯=21
证明:设 A = 1 − 1 + 1 − 1 + 1 − 1 + … A=1-1+1-1+1-1+\dots A=1−1+1−1+1−1+…,则:
∴ A = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + … = 1 − ( 1 − 1 + 1 − 1 + 1 − 1 + … ) = 1 − A \begin{aligned}\therefore A&=1-1+1-1+1-1+1-1+\dots\\&=1-(1-1+1-1+1-1+\dots)\\&=1-A\end{aligned} ∴A=1−1+1−1+1−1+1−1+…=1−(1−1+1−1+1−1+…)=1−A
∴ A = 1 2 \therefore A=\cfrac{1}{2} ∴A=21
-
1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + ⋯ = 1 4 1-2+3-4+5-6+7-8+\dots=\cfrac{1}{4} 1−2+3−4+5−6+7−8+⋯=41
证明:设 B = 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + … B=1-2+3-4+5-6+7-8+\dots B=1−2+3−4+5−6+7−8+…,则:
∴ 2 × B = 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + ⋯ + 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + … = 1 + ( − 2 + 1 ) + ( 3 − 2 ) + ( − 4 + 3 ) + ( 5 − 4 ) + ( − 6 + 5 ) + … = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + … = 1 2 \begin{aligned}\therefore 2\times B&=1-2+3-4+5-6+7-8+\dots+1-2+3-4+5-6+7-8+\dots\\&=1+(-2+1)+(3-2)+(-4+3)+(5-4)+(-6+5)+\dots\\&=1-1+1-1+1-1+1-1+\dots\\&=\cfrac{1}{2}\end{aligned} ∴2×B=1−2+3−4+5−6+7−8+⋯+1−2+3−4+5−6+7−8+…=1+(−2+1)+(3−2)+(−4+3)+(5−4)+(−6+5)+…=1−1+1−1+1−1+1−1+…=21
∴ B = 1 4 \therefore B=\cfrac{1}{4} ∴B=41
好了,有了这些基础知识,我们就可以开始算 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + … 1+2+3+4+5+6+7+8+\dots 1+2+3+4+5+6+7+8+… 了。
设 C = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + … C=1+2+3+4+5+6+7+8+\dots C=1+2+3+4+5+6+7+8+…,则:
∴ 4 × C = 4 + 8 + 12 + 16 + 20 + … \therefore4\times C=4+8+12+16+20+\dots ∴4×C=4+8+12+16+20+…
∴ C − 4 × C = 1 + 2 + 3 + 4 + 5 + 6 + ⋯ − 4 − 8 − 12 − 16 − 20 − … = 1 + ( 2 − 4 ) + 3 + ( 4 − 8 ) + … = 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + … = 1 4 \begin{aligned}\therefore C-4\times C&=1+2+3+4+5+6+\dots-4-8-12-16-20-\dots\\&=1+(2-4)+3+(4-8)+\dots\\&=1-2+3-4+5-6+7-8+\dots\\&=\cfrac{1}{4}\end{aligned} ∴C−4×C=1+2+3+4+5+6+⋯−4−8−12−16−20−…=1+(2−4)+3+(4−8)+…=1−2+3−4+5−6+7−8+…=41
∴ C = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ⋯ = − 1 12 \therefore C=1+2+3+4+5+6+7+8+\dots=-\cfrac{1}{12} ∴C=1+2+3+4+5+6+7+8+⋯=−121
其实学过高数的同学早就已经发现问题了:我们一开始求得这个数列 1 − 1 + 1 − 1 + 1 − 1 + … 1-1+1-1+1-1+\dots 1−1+1−1+1−1+… 本身就是没有意义的,因为在高数中要算一个无穷级数的和首先就得满足收敛。收敛指什么呢?
收敛就是指一个无穷级数求和的函数图像会逐渐平缓,最终趋于一条直线,比如 1 1 − 1 3 + 1 5 − 1 7 + … \cfrac{1}{1}-\cfrac{1}{3}+\cfrac{1}{5}-\cfrac{1}{7}+\dots 11−31+51−71+… 的函数图像就长这样:
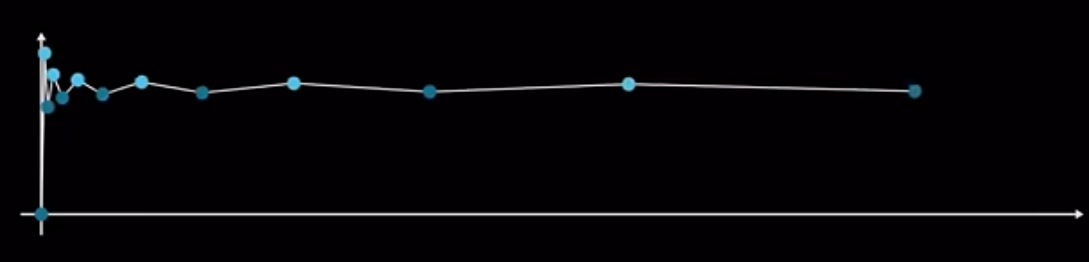
我们会发现它逐渐趋向于一条直线,所以我们可以算出来它的值就是 π 4 \cfrac{\pi}{4} 4π。
而 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + … 1-1+1-1+1-1+1-1+\dots 1−1+1−1+1−1+1−1+… 就不一样了,它的函数图像明显长这样:
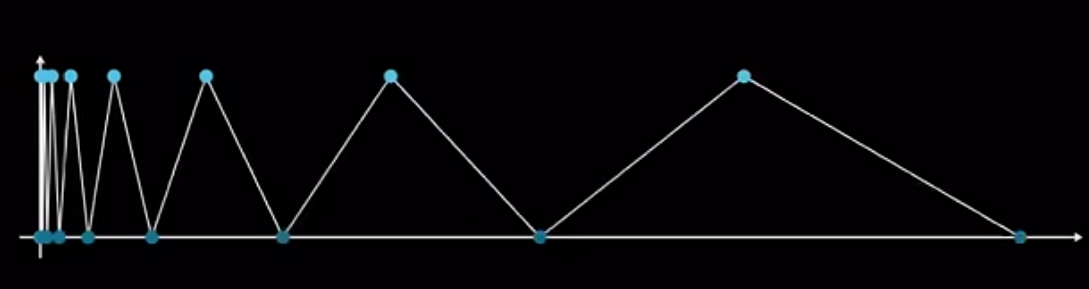
一直在 1 1 1 和 0 0 0 之间跳动,所以说我们并不能算出 1 − 1 + 1 − 1 + 1 − 1 + … 1-1+1-1+1-1+\dots 1−1+1−1+1−1+… 到底等于多少。
再比如说 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + … 1+1+1+1+1+1+1+1+\dots 1+1+1+1+1+1+1+1+… 等于多少呢?
我们会发现它的函数图像长这样:
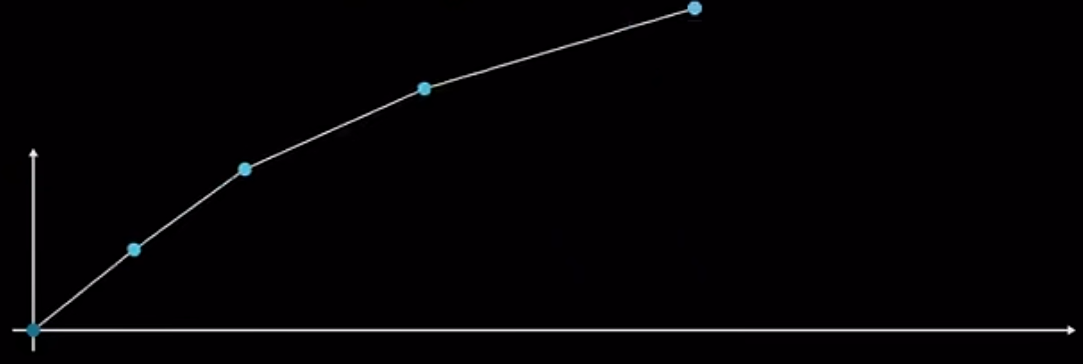
逐渐王远处跑,所以我们也是算不出来这个式子到底等于几的。
但这就有很多人反驳了:那作者你怎么给我解释一下卡西米尔效应?
卡西米尔效应,其实就是在真空中把两块铁板靠的很近很近,那么这两块铁板之间就会因为量子的涨落而带来一定的斥力,而这个斥力的大小与量子场内的驻波的波节的个数成正比。这个力的大小之间的比值就是驻波的波节的个数。也就是他们之间的斥力为 F + 2 F + 3 F + … F+2F+3F+\dots F+2F+3F+…。
但是物理学家们不管是实际验证还是用其他方法计算,都发现了一个惊人的事实:这个几个力的合力竟然朝里,且大小就是 1 12 F \cfrac{1}{12}F 121F。
再比如说黎曼函数 ζ ( z ) = 1 1 z + 1 2 z + 1 3 z + 1 4 z + … , Re ( z ) > 1 \zeta(z)=\cfrac{1}{1^z}+\cfrac{1}{2^z}+\cfrac{1}{3^z}+\cfrac{1}{4^z}+\dots,\operatorname{Re}(z)>1 ζ(z)=1z1+2z1+3z1+4z1+…,Re(z)>1,那么当我们把 z = − 1 z=-1 z=−1 时,原式就成了自然数的求和,而这个黎曼函数算出来的值就是 − 1 12 -\cfrac{1}{12} −121。
所以一会成立一会又不成立,这个式子到底等于多少呢?作者也不知道,建议大家去看看这个视频,或许能帮助你理解。(主要是作者的脑容量不够了……)





















 1810
1810

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








