插个小广告:没看过“垫付你的常识系列一”的同学可以点击此处进入
问题描述
现在有一个箱子,里面装着 10 10 10 个球,有红球有绿球,我们并不知道这个箱子里有多少个红球、多少个绿球,现在我从箱子里摸出了一个红球,那么请问第二次摸到红球的概率大还是绿球的概率大?
解析
你可能感觉箱子里的红球变少了,摸到绿球的概率应该会比红球大一点吧。但实际上下次摸到绿球的概率仍然比红球小,而且小得多。
我们可以这么思考:因为我们一开始就摸出了一个红球,所以说这个箱子里应该有很多红球,而这个箱子里有很多红球恰恰说明了我们下次摸到红球的概率大。这就像是有个人坑了你,你不会觉得他今天坑了我以后就会少坑点我,恰恰相反,这说明他就是个坑人。(在线提醒:你们以后如果遇到了这样的人千万不要和他交朋友。)
那这个概率又是怎么算的呢?我们可以这样想,首先从红球和绿球之间分隔开:

然后我们拿走了其中一个红球,相当于把红球又分成了两份:
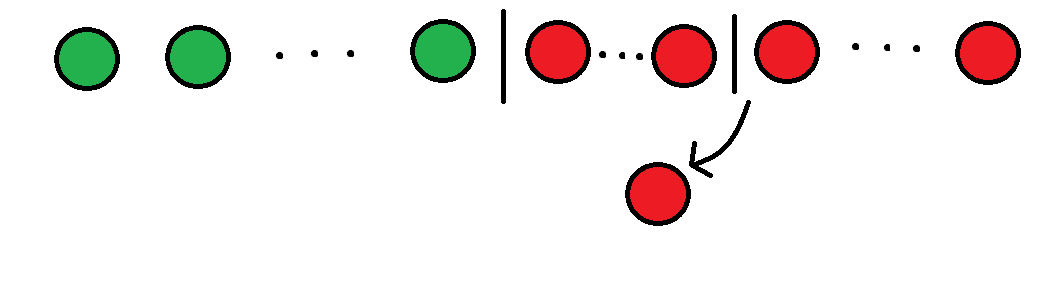
于是就成了一共 9 9 9 个球分成 3 3 3 份,其中 2 2 2 份是红球,求抽到红球的概率。这一听就很像 2 3 \cfrac{2}{3} 32 对吧?
如果你觉得这不科学,你可以用概率暴算( N N N 表示总球数,是定值, n n n 表示红球个数):
P ( 第二次抽到红球 ) = P ( 连续两次抽到红球 ) P ( 第一次抽到红球 ) = ∑ n = 1 N 1 N + 1 × n ⋅ ( n − 1 ) N ⋅ ( N − 1 ) ∑ n = 1 N 1 N + 1 ⋅ n N = 2 3 \begin{align}\operatorname{P}(\text{第二次抽到红球})&=\cfrac{\operatorname{P}(\text{连续两次抽到红球})}{\operatorname{P}(\text{第一次抽到红球})}\\&=\cfrac{\sum_{n=1}^N\cfrac{1}{N+1}\times\cfrac{n\cdot(n-1)}{N\cdot(N-1)}}{\sum_{n=1}^N\cfrac{1}{N+1}\cdot\cfrac{n}{N}}\\&=\cfrac{2}{3}\end{align} P(第二次抽到红球)=P(第一次抽到红球)P(连续两次抽到红球)=∑n=1NN+11⋅Nn∑n=1NN+11×N⋅(N−1)n⋅(n−1)=32
如果你觉得数学太难了,也可以自己动手实操(俗话说得好:自己动手,丰衣足食。),答案也是 2 3 \cfrac{2}{3} 32。
如果你先自己动手太麻烦,也不妨写个 python 程序,答案还是 2 3 \cfrac{2}{3} 32。
而这还不是它最反直觉的地方,它最反直觉的地方在于它不管在红球有几个的情况下都一样,甚至只有两个红球时也是这个答案。所以下次在考试时看到前三题都选 A,这说明是第四题肯定不能选 A,还是出题老师很喜欢 A 呢?
本文灵感来源视频:前三道选择题都选A,第四道你敢选A吗?。





















 425
425

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








