博客围绕无人车激光雷达BEV图绘制展开，因原始激光雷达点处于车体局部坐标系，需转换到像素坐标系。介绍了二维坐标系变换，包括翻转和平移两步，给出了相应矩阵公式，合并后得到最终坐标变换公式，还提供了C++代码及旋转平移矩阵公式。
1.动机
在项目中，我们常常需要绘制无人车激光雷达的BEV图。而原始激光雷达的点所处的坐标是车体局部坐标系（简称为vehiclepose）。所以就涉及到一个坐标系的转换，如图所示，由vehiclepose坐标系（记为O1）转换到pixel坐标系（记为O4）。
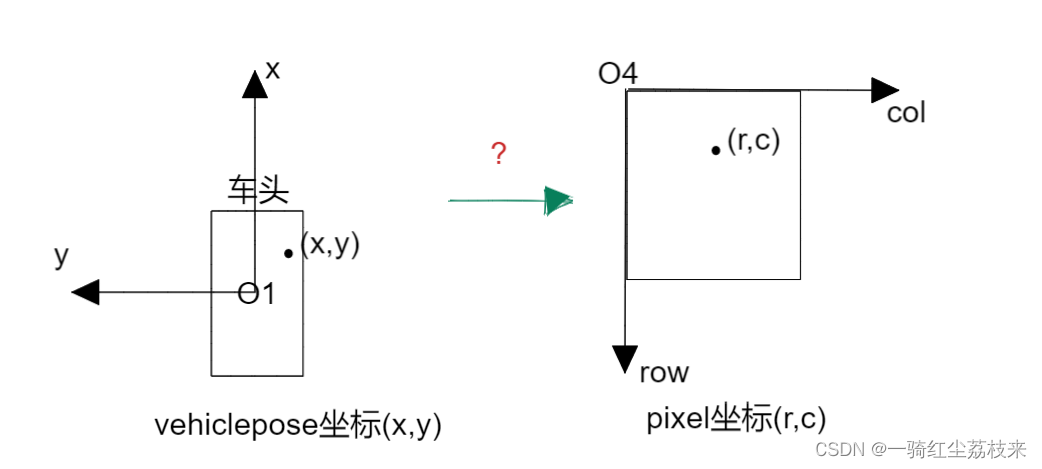
这里直接给出变换公式：
{
R=−x1+dRC=−y1+dC \begin{cases} R=-x1+dR \\ C=-y1+dC \end{cases} {
R=−x1+dRC=−y1+dC
可以看到实际上计算非常简单。感兴趣可以看下面的细节。
2.细节
二维坐标系的变换涉及到翻转和平移。下面就分成翻转和平移 2步完成这个转换：
2.1翻转
首先需要由O1，xy坐标轴都翻转，变成O2：
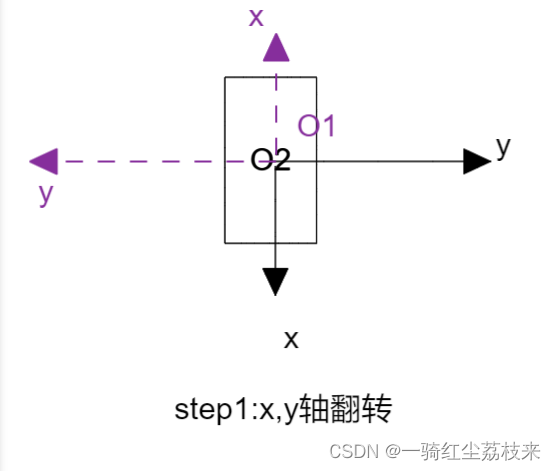
用翻转矩阵表达就是：
[x2y2]=[−100−1][x1y1]\begin{bmatrix} x2 \\ y2 \end{bmatrix}=\begin{bmatrix} -1& 0\\ 0 & -1\end{bmatrix}\begin{bmatrix} x1 \\ y1 \end{bmatrix}[x2y2]=[−100−1
最低0.47元/天 解锁文章
扫一扫
970
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
