概率机器人_C3_卡尔曼滤波——噪声模型初始化问题

问题：噪声矩阵Q,R 的确定，决定了系统的能否收敛，收敛速度。如何确定呢？

---

数学基础：https://wenku.baidu.com/view/0ba46c5280eb6294dc886c32.html

x 是关于t的函数， t 时刻开始， x(t) 泰勒展开为

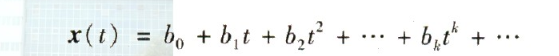
t= 0, x(0)=bo

右边写成x(t+1)= x'= 

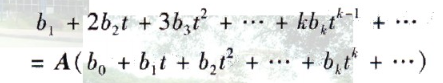
系统相同， 得到 b0*A=b1

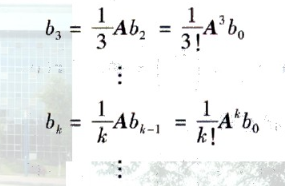
带回，x(t),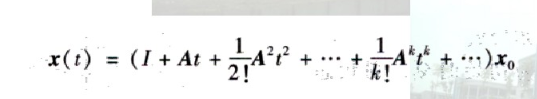 

0--t 时间的状态转移矩阵为 括号内的数。可以记做

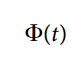
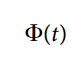和 A 矩阵（动态矩阵）维度相同，如果是2*2，  如何表示状态误差呢？

 

---