【教程4＞第5章＞第3节】通过MATLAB分析不同长度PN序列的自相关性能

已于 2025-01-09 05:52:05 修改
阅读量265 收藏 3
点赞数 1
分类专栏： # 第5章·通信—帧同步相位同步位同步 文章标签： fpga开发 PN序列 m序列 帧同步 教程4 matlab
于 2025-01-02 23:38:34 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/ccsss22/article/details/144897405
版权

 欢迎订阅FPGA/MATLAB/Simulink系列教程

《★教程1:matlab入门100例》

《★教程2:fpga入门100例》

《★教程3:simulink入门60例》

《★教程4:FPGA/MATLAB/Simulink联合开发入门与进阶X例》

目录

1.软件版本

2.理论简介

2.1 PN序列概述

2.2 通过m序列产生PN序列

2.3 不同长度PN序列的自相关性能

3.通过MATLAB产生PN序列

4.不通长度PN序列的抗干扰性能分析

4.1 PN长度=31

4.2 PN长度=63

4.3 PN长度=127

4.4 PN长度=255

1.软件版本

vivado2019.2，matlab2022a

2.理论简介

2.1 PN序列概述

       PN序列即伪随机序列，是一种由近似随机但实际有一定规律的周期性二进制序列组成的常用地址码。其具有类似于随机序列的基本特性，貌似随机但实际上是可通过特定的规则或算法生成和复现。

       PN 序列具有近似于白噪声的自相关特性，即除了在零时延处自相关函数有一个尖锐的峰值外，在其他时延处的自相关值都接近于零。同时，PN 序列是周期序列，这是它与真正随机序列的重要区别之一。

2.2 通过m序列产生PN序列

        m序列是最长线性反馈移位寄存器序列（Maximum - length Linear Feedback Shift Register Sequence）的简称。它是一种由线性反馈移位寄存器（LFSR）产生的伪随机序列。m 序列的周期2^n-1，其中n是移位寄存器的级数。其结构如下图所示：

2.3 不同长度PN序列的自相关性能

       自相关函数在零时延处有一个主峰，表示序列与自身完全对齐时的相关性最大。由于长度较短，在非零时延处的自相关旁瓣相对较大，与主峰的比值相对较高。例如，一个周期为7的m序列，其自相关函数在非零时延处的旁瓣可能会比较明显，虽然旁瓣值小于主峰，但在一些对自相关性能要求苛刻的应用中可能会产生干扰。

       在同步检测方面，短PN 序列的短周期有利于快速同步，因为接收端不需要等待太长时间就可以遍历一个完整的周期来寻找同步点。然而，其较大的自相关旁瓣可能会导致在噪声环境下产生误判。而长PN序列虽然周期长，同步时间长，但一旦同步成功，其良好的自相关性能可以提供非常高的同步精度。在抗干扰方面，长PN 序列可以有效地抵抗多径干扰、窄带干扰和同频干扰等多种干扰。

      因此，在实际设计中，我们需要根据信道的情况，来设计最佳长度的PN序列。在本课程中，我们将通过MATLAB来分析不同长度PN序列的抗干扰性能。

3.通过MATLAB产生PN序列

首先定义一个基于m序列的伪随机序列子函数为：

function [y]=mseq(X)
 
m=length(X);
len=2^m-1;  
temp=0;  
y=zeros(1,len);  
regs = [1 zeros(1, m-2) 1];  
for i=1:len
    y(i)=regs(m);
    temp = mod(sum(X.*regs) , 2);  
    regs(2:length(regs)) = regs(1:length(regs)-1); % 移位
    regs(1)=temp; % 异或 
end
%补充一个数据，数据到2的幂次方
y=[y];
end

然后我们调用该子函数：

clc;
clear;
close all;
warning off;
rng('default');


[PN1]=mseq([0,0,0,1,1,0]);

figure;
stem(PN1)
ylim([0,1.2]);

运行后，得到如下的结果：

这个就是一个长度为63的PN序列，即：

1,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,1,1,1,0,1,0,0,0,1,1,1,0,0,1,0,0,1,0,1,1,0,1,1,1,0,1,1,0,0,1,1,0,1,0,1,0,1,1,1,1,1,1,0,0,0,0,0

4.不通长度PN序列的抗干扰性能分析

这里，我们采用AWGN信道作为分析PN性能信道模型。首先我们先编写如下的MATLAB程序：

clc;
clear;
close all;
warning off;
rng('default');


[PN1]=2*mseq([0,0,0,0,1,1])-1;

figure;
stem(PN1)
ylim([0,1.2]);


data1 = [randn(1,256),PN1,randn(1,512)];

PK1 = xcorr(data1,PN1);
PK2 = PK1.^2;

figure;
subplot(211);
plot(PK1)
title('peak');
subplot(212);
plot(PK2)
title('peak^2');

运行后，我们可以看到如下仿真结果：

       第一个图PN序列的自相关运算后得到的相关峰，第二个是相关峰的平方。一般情况下，峰值通过平方运算后，可以进一步增加相关峰的性能。

        下面我们来分析不同长度下PN序列的自相关性性能。

4.1 PN长度=31

先编写matlab程序：

% 清除命令行窗口内容
clc;
% 清除工作空间中的变量
clear;
% 关闭所有图形窗口
close all;
% 关闭警告信息
warning off;
% 设置随机数生成器的种子为默认值
rng('default');


% 生成一个 m 序列并转换为 +1 和 -1 的形式，可能用于后续处理
[PN1]=2*mseq([0,0,0,1,1])-1;


% 绘制 PN1 的离散序列图
figure;
stem(PN1)
% 设置 y 轴范围
ylim([0,1.2]);


% 组合随机数据、PN1 序列和更多随机数据形成新的数据序列
data1 = [randn(1,256),PN1,randn(1,512)];


% 给 data1 加入噪声，信噪比为 -5dB，'measured' 表示根据信号的功率来计算噪声功率
datan1= awgn(data1,-5,'measured');
% 计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 创建一个新的图形窗口并划分为 4x2 的子图布局，在第一个子图中绘制 PK1
figure;
subplot(421);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 -5dB
title('peak,SNR=-5');
% 在第二个子图中绘制 PK2
subplot(422);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 0dB
datan1= awgn(data1,0,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第三个子图中绘制 PK1
subplot(423);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 0dB
title('peak,SNR=0');
% 在第四个子图中绘制 PK2
subplot(424);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 5dB
datan1= awgn(data1,5,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第五个子图中绘制 PK1
subplot(425);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 5dB
title('peak,SNR=5');
% 在第六个子图中绘制 PK2
subplot(426);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 10dB
datan1= awgn(data1,10,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第七个子图中绘制 PK1
subplot(427);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 10dB
title('peak,SNR=10');
% 在第八个子图中绘制 PK2
subplot(428);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');

运行后结果如下：

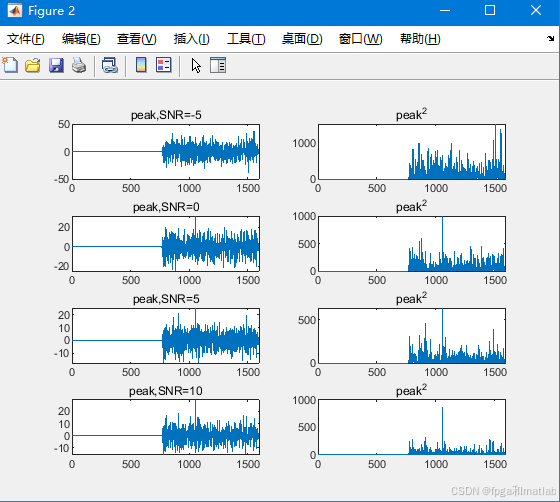
可以看到，PN长度为31时，SNR大于10后，出现了相关峰，但是其峰值较小，且峰值附近的噪声也较大。在实际应用中会导致错误检测。当SNR小于10时，基本没法检测到明显的相关峰。

4.2 PN长度=63

 将上面的matlab程序改为：

% 清除命令行窗口内容
clc;
% 清除工作空间中的变量
clear;
% 关闭所有图形窗口
close all;
% 关闭警告信息
warning off;
% 设置随机数生成器的种子为默认值
rng('default');


% 生成一个 m 序列并转换为 +1 和 -1 的形式，可能用于后续处理
[PN1]=2*mseq([0,0,0,0,1,1])-1;


% 绘制 PN1 的离散序列图
figure;
stem(PN1)
% 设置 y 轴范围
ylim([0,1.2]);


% 组合随机数据、PN1 序列和更多随机数据形成新的数据序列
data1 = [randn(1,256),PN1,randn(1,512)];


% 给 data1 加入噪声，信噪比为 -5dB，'measured' 表示根据信号的功率来计算噪声功率
datan1= awgn(data1,-5,'measured');
% 计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 创建一个新的图形窗口并划分为 4x2 的子图布局，在第一个子图中绘制 PK1
figure;
subplot(421);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 -5dB
title('peak,SNR=-5');
% 在第二个子图中绘制 PK2
subplot(422);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 0dB
datan1= awgn(data1,0,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第三个子图中绘制 PK1
subplot(423);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 0dB
title('peak,SNR=0');
% 在第四个子图中绘制 PK2
subplot(424);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 5dB
datan1= awgn(data1,5,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第五个子图中绘制 PK1
subplot(425);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 5dB
title('peak,SNR=5');
% 在第六个子图中绘制 PK2
subplot(426);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 10dB
datan1= awgn(data1,10,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第七个子图中绘制 PK1
subplot(427);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 10dB
title('peak,SNR=10');
% 在第八个子图中绘制 PK2
subplot(428);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');

 运行后结果如下：

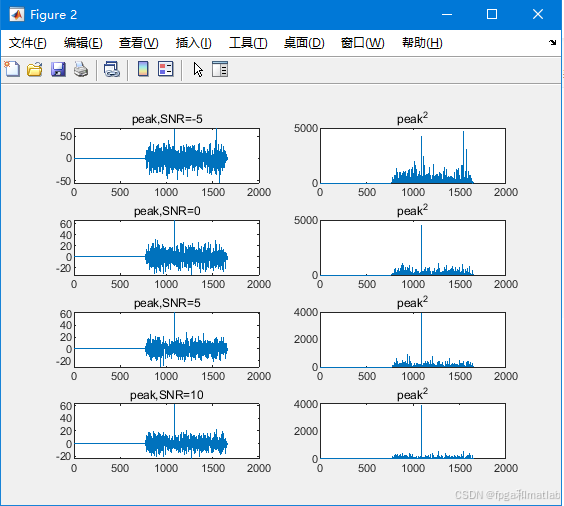
当PN长度为63时，SNR大于0，均可以获得较为明显的相关峰，而当SNR<=0时，相关峰无法精确识别。

4.3 PN长度=127

 将上面的matlab程序改为：

% 清除命令行窗口内容
clc;
% 清除工作空间中的变量
clear;
% 关闭所有图形窗口
close all;
% 关闭警告信息
warning off;
% 设置随机数生成器的种子为默认值
rng('default');


% 生成一个 m 序列并转换为 +1 和 -1 的形式，可能用于后续处理
[PN1]=2*mseq([0,0,0,0,0,1,1])-1;


% 绘制 PN1 的离散序列图
figure;
stem(PN1)
% 设置 y 轴范围
ylim([0,1.2]);


% 组合随机数据、PN1 序列和更多随机数据形成新的数据序列
data1 = [randn(1,256),PN1,randn(1,512)];


% 给 data1 加入噪声，信噪比为 -5dB，'measured' 表示根据信号的功率来计算噪声功率
datan1= awgn(data1,-5,'measured');
% 计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 创建一个新的图形窗口并划分为 4x2 的子图布局，在第一个子图中绘制 PK1
figure;
subplot(421);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 -5dB
title('peak,SNR=-5');
% 在第二个子图中绘制 PK2
subplot(422);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 0dB
datan1= awgn(data1,0,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第三个子图中绘制 PK1
subplot(423);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 0dB
title('peak,SNR=0');
% 在第四个子图中绘制 PK2
subplot(424);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 5dB
datan1= awgn(data1,5,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第五个子图中绘制 PK1
subplot(425);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 5dB
title('peak,SNR=5');
% 在第六个子图中绘制 PK2
subplot(426);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 10dB
datan1= awgn(data1,10,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第七个子图中绘制 PK1
subplot(427);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 10dB
title('peak,SNR=10');
% 在第八个子图中绘制 PK2
subplot(428);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');

 运行后结果如下：

可以看到，PN长度为127时，在不同SNR下，均可以获得较为明显的相关峰。

4.4 PN长度=255

将上面的matlab程序改为：

% 清除命令行窗口内容
clc;
% 清除工作空间中的变量
clear;
% 关闭所有图形窗口
close all;
% 关闭警告信息
warning off;
% 设置随机数生成器的种子为默认值
rng('default');


% 生成一个 m 序列并转换为 +1 和 -1 的形式，可能用于后续处理
[PN1]=2*mseq([0,0,0,0,1,1,1,1])-1;


% 绘制 PN1 的离散序列图
figure;
stem(PN1)
% 设置 y 轴范围
ylim([0,1.2]);


% 组合随机数据、PN1 序列和更多随机数据形成新的数据序列
data1 = [randn(1,256),PN1,randn(1,512)];


% 给 data1 加入噪声，信噪比为 -5dB，'measured' 表示根据信号的功率来计算噪声功率
datan1= awgn(data1,-5,'measured');
% 计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 创建一个新的图形窗口并划分为 4x2 的子图布局，在第一个子图中绘制 PK1
figure;
subplot(421);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 -5dB
title('peak,SNR=-5');
% 在第二个子图中绘制 PK2
subplot(422);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 0dB
datan1= awgn(data1,0,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第三个子图中绘制 PK1
subplot(423);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 0dB
title('peak,SNR=0');
% 在第四个子图中绘制 PK2
subplot(424);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 5dB
datan1= awgn(data1,5,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第五个子图中绘制 PK1
subplot(425);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 5dB
title('peak,SNR=5');
% 在第六个子图中绘制 PK2
subplot(426);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');



% 给 data1 加入噪声，信噪比为 10dB
datan1= awgn(data1,10,'measured');
% 重新计算 data1 与 PN1 的互相关
PK1 = xcorr(datan1,PN1);
% 对互相关结果进行平方运算
PK2 = PK1.^2;


% 在第七个子图中绘制 PK1
subplot(427);
plot(PK1)
% 为该子图添加标题，表明当前 SNR 为 10dB
title('peak,SNR=10');
% 在第八个子图中绘制 PK2
subplot(428);
plot(PK2)
% 为该子图添加标题，表明当前是 PK1 的平方
title('peak^2');

 运行后结果如下：

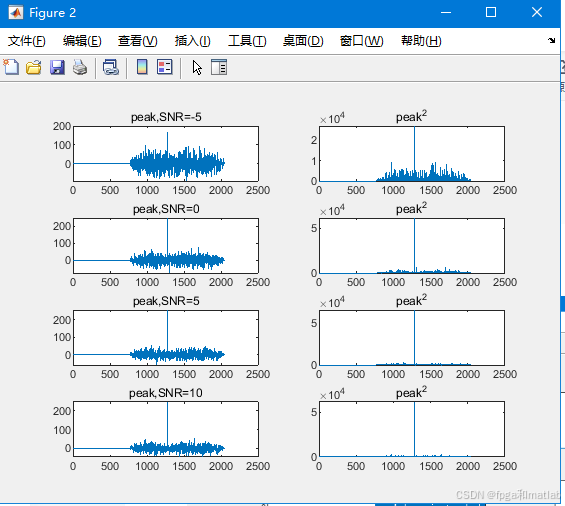
可以看到，PN长度为255时，在不同SNR下，均可以获得较为明显的相关峰。

       综上所述，在一般的通信系统中(满足SNR>0时正常通信)，选择PN长度为63就可以满足需求。因此在本课题中，我们选择长度为63的PN序列。

【教程4＞第5章＞第7节】通过FPGA实现基带帧数据与本地PN序列做相关运算得到相关峰
FPGA/MATLAB学习教程/源码/项目合作开发
01-10 624
基带数据和本地的PN序列做相关运算，也称之为伪码匹配滤波。可以理解为本地的PN序列为滤波器的系数，然后对输入的基带数据做滤波。通过伪码匹配滤波，我们可以利用本地 PN 序列和基带帧数据进行相关运算。
【教程4＞第5章＞第4节】通过FPGA实现数据帧插入PN序列组帧
FPGA/MATLAB学习教程/源码/项目合作开发
01-02 137
首先，我们要对输入的数据进行组帧，每一帧数据的结构如下图所示：其中，63bit的PN序列可以作为一种帧的识别码。不同的通信系统可以采用不同的 PN 序列作为帧头，通过识别这个 PN 序列，接收端可以判断出数据是否来自正确的发送源或者是否属于正确的通信流程。1024bit 的数据部分是用于承载实际要传输的信息的。在发送端，首先生成 63bit 的 PN 序列作为帧头，然后将 1024bit 的数据部分紧跟在帧头后面，从而组成一帧完整的数据。
PN序列的产生及其自相关特性仿真
10-29
PN序列的产生及其自相关特性仿真，用于信源信号的调制
PN序列自相关特性分析
Prozzz777
11-28 1万+
PN序列就是伪随机序列（Pseudo—Noise Code），所谓的伪就是说这个序列随机性很强，统计特性很好但并不是真正的随机数，体现PN序列具有周期性。PN序列是由通过线性反馈移位寄存器实现的，移位寄存器的级数决定了其周期性的长短。 Matlab 代码： 参考：https://wenku.baidu.com/view/e44cdf6227d3240c8447ef44.html clear all...
使用LFSR产生PN序列
最新发布
lzr232的博客
04-22 321
使用LFSR生成PN随机序列
PN序列的产生以及相关函数的计算
山山 | 33
03-18 9530
求 PN 序列并极化（给定初始序列[1 0 0 0 0 0]），c(n)代表序列第 n 个值，c(0)代表 c(N) function cout=c(L,n) head=[[1 0 0 0 0 1],%[6,1] [1 1 0 0 1 1],%[6,5,2,1] [1 0 0 1 1 1]];%[6,5,4,1] head_L=logic...
数字通信——扩频调制
weixin_52743423的博客
06-03 1838
Communication Systems -4ed - Haykin 数字通信笔记
PN序列产生程序--m序列
10-25
适合初学DSSS信号产生
【教程4＞第5章＞第2节】基于PN序列的帧同步系统理论概述和FPGA设计构架
FPGA/MATLAB学习教程/源码/项目合作开发
01-02 242
在本课程中，我们以QPSK信号为例进行学习。在QPSK发射端，对基带数据加入PN序列，和数据组成帧结构，然后通过成型滤波得到QPSK映射数据。接收端则对QPSK信号进行解调，然后对恢复的基带数据做PN伪码匹配滤波得到相关峰，最后对相关峰进行峰值检测，从而完成帧同步。本小节，我们就帧同步的具体原理和FPGA设计构架做一个整体学习。
PN 序列生成：生成长度为 31 的 m 序列。-matlab开发
06-01
总之，MATLAB是实现PN序列生成的理想平台，通过理解和运用上述方法，我们可以生成具有特定长度和属性的m序列，为无线通信中的各种功能提供基础。在下载并解压`PN_sequence_generation.zip`文件后，你可以找到实现这...
m序列的产生原理及其性质
Jackiezhang1993的博客
03-31 1万+
1 LFSR 1.1 定义 线性反馈移位寄存器（LFSR，linear feedback shift register）由n个移位寄存器和若干个异或门组成（各个反馈系数路径只由模二加/异或组成为线性反馈），如下图所示。n级移位寄存器共有2^n个状态，除去全0状态外还剩种状态，故一个n级线性反馈移位寄存器产生的最长周期为。 LFSR有2种形式，分别为异或门内/外接LFSR，如下图。其中，有n级移位寄存器...
matlab—PN序列代码
05-06
PN序列的代码。输入生成多项式可生成PN序列。测试可用
PN序列生成函数：该函数生成PN序列（最大长度序列）-matlab开发
06-01
要使用这个函数，只需定义一个变量，比如 var， var = pnseq(a, b, c); 对于 a、b 和 c，请参阅 zip 文件
pn9序列生成器
01-17
用VHDL编写的pn9序列生成器 library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; entity pn_9 is port(clk,rst:in std_logic; pnout:out std_logic ); end pn_9; architecture behavior of pn_9 is signal shifter :std_logic_vector(8 downto 0); begin pnout<=shifter(8); process(rst,clk)
用MATLAB产生m序列+互相关、自相关特性分析
babala的博客
03-16 2万+
题目 考虑周期N=63的两个pn序列，一个序列的反馈抽头为[6,1]，另一个序列的反馈抽头为[6,5,2,1]。 (a) 计算这两个序列的互相关函数和自相关函数 (b) 比较(a)中所得的互相关函数和序列[6,5,2,1]与镜像序列[6,5,4,1]之间的互相关函数。 主体代码 clc,clear; N=63;%周期为63 %产生反馈抽头，从左到右依次表示寄存器1,2,3,4,5,6 p1=[1,...
m序列产生原理及其性质
热门推荐
kinsun
05-06 14万+
m序列产生原理及其性质 一、m序列的简介 1、m序列是最长线性移位寄存器序列的简称。顾名思义，m序列是由多级移位寄存器或其延迟元件通过线性反馈产生的最长的码序列。在二进制移位寄存器中，若n为移位寄存器的级数，n级移位寄存器共有 2n 个状态，除去全0状态外还剩下 2n-1 中状态，因此它能产生的最大长度的码序列为 2n-1 位，也就是说，一个n级线性反馈移位寄存器产生的最长周期等于 2n-1 ...
伪随机序列——m序列及MATLAB仿真
明天你好的博客
11-05 1万+
在通信系统中的随机噪声会使模拟信号产生失真和使数字信号出现误码，并且，它还是限制信道容量的一个重要因素。因此人们经常希望消除或减小通信系统中的随机噪声。另外，有时人们会希望获得随机噪声。例如，在实验室中对通信设备或系统性能进行测试时，可能要故意加人一定的随机噪声。伪随机噪声具有类似于随机噪声的某些统计特性，同时又能够重复产生。由于它具有随机噪声的优点，又避免了随机噪声的缺点，因此获得了日益广泛的实际应用。目前广泛应用的伪随机噪声都是由周期性数字序列经过滤波等处理后得出的。
伽罗华域下的伪随机序列图像编码（一）
视觉小新的博客
03-28 2575
最近看了一篇TPAMI文章Determining Both Surface Position and Orientation in Structured-Light-Based Sensing ，是用伪随机序列编码图像，图像是这样的： 最后利用该编码图像重构出来的结果是这样的 具体怎么编码呢？怎么得到最终的结果呢？今天先简单从下面三部分介绍： 1，伪随机序列 2，伽罗华域...
通信原理_时域相关_01（MATLAB_xcorr）
flypassion的博客
12-25 4695
在通信系统中，捕获、同步等过程都会涉及到相关处理，而相关又分为时域相关和频域相关，这里主要对时域相关的处理进行简单介绍。 时域相关指的是本地码（PN码，M码等具有良好的自相关性的码）和接受到的信号进行相关处理，通过相关值来判断相关性的强弱，进而确定相关位置（即获得捕获位置、同步位置等）。时域相关计算本质就是本地码和输入信号乘积求和（复数信号是信号和本地码的共轭相乘求和）算出相关值。 相关计算和...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

fpga和matlab

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值