OFDM信道估计matlab误码率仿真,对比LS线性插值,LS样条spline插值以及MMSE

最新推荐文章于 2024-12-15 20:09:35 发布

fpga和matlab

最新推荐文章于 2024-12-15 20:09:35 发布

阅读量1.3k

点赞数 6

分类专栏：部分上传资源仿真展示与分析 MATLAB 板块1:通信与信号处理文章标签： matlab OFDM信道估计 LS线性插值 LS样条spline插值 MMSE

本文链接：https://blog.youkuaiyun.com/ccsss22/article/details/139013958

版权

MATLAB 同时被 3 个专栏收录

1617 篇文章

订阅专栏

板块1:通信与信号处理

625 篇文章

订阅专栏

部分上传资源仿真展示与分析

136 篇文章

订阅专栏

OFDM（Orthogonal Frequency Division Multiplexing，正交频分复用）系统因其高效的数据传输能力和对抗多径传播的能力而广泛应用于无线通信领域。在OFDM系统中，信道估计是至关重要的，因为它直接影响到接收端对信号的正确解调。下面将深入探讨几种常见的信道估计方法：最小二乘法（Least Squares, LS）、LS线性插值、LS样条Spline插值以及最小均方误差（Minimum Mean Square Error, MMSE）方法。

1. 最小二乘法（LS）信道估计

最小二乘法是最基础的信道估计方法，它通过最小化实际观测值与模型预测值之间的平方差来估计信道。在OFDM系统中，已知导频符号（pilot symbols）及其对应的已知传输数据，可以建立如下线性模型：

其中，y 是接收到的含有噪声的导频符号向量，X 是已知的导频位置指示矩阵，ℎh 是待估计的信道频率响应向量，n 是加性高斯白噪声向量。LS估计h^LS 可以通过解下面的优化问题得到：

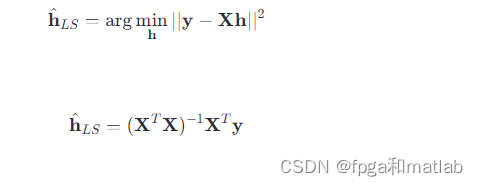
2. LS线性插值

由于在实际的OFDM系统中，导频不是连续分布的，因此直接应用LS估计会导致非导频位置的信道未知。线性插值是在已知的导频点之间假设信道频率响应呈线性变化，从而估计未知点的信道值。对于两个相邻的导频点 i 和 i+1，其间的任意一点 k 的信道估计值可通过线性内插公式得到：

3. LS样条Spline插值

相比于线性插值，样条Spline插值提供了一种更平滑的信道估计方法。Spline插值通过在一系列控制点上定义多项式函数，并确保这些函数在连接点处具有连续的一阶、二阶甚至更高阶导数，从而获得更为平滑的曲线。对于一维的信道频率响应估计，自然三次样条（natural cubic spline）是最常用的。其基本思想是在每个导频点间定义一个三次多项式，同时保证每两个相邻多项式在边界处的值、一阶导数和二阶导数连续。具体的数学表达较为复杂，涉及解一个带有边界条件的线性系统。

4. 最小均方误差（MMSE）信道估计

MMSE估计考虑了信道统计特性，相比LS估计能提供更好的性能，尤其是在噪声较大的环境中。MMSE估计的目标是找到一个估计值h^MMSE，使得估计误差的均方值最小：

在已知信道统计特性的前提下，MMSE估计器可以表示为：

这里Rhh 是信道频率响应的协方差矩阵，σ2 是噪声方差，I 是单位矩阵。

5. MATLAB核心程序

....................................................
for t=1:itr
         %%LS估计
         H_est = LS_CE(Y,Xp,loc,Nfft,Nps,'linear');
         err=(H-H_est)*(H-H_est)';
         z=[z err/(Nfft*Nsym)];
         
         %%LS估计
         h_est = ifft(H_est);
         h_DFT = h_est(1:ch_length);
         H_DFT = fft(h_DFT,Nfft); 
         err=(H-H_DFT)*(H-H_DFT)';
         z3=[z3 err/(Nfft*Nsym)];
         
         %%LS估计
         H_est = LS_CE(Y,Xp,loc,Nfft,Nps,'spline');
         err=(H-H_est)*(H-H_est)';
         z1=[z1 err/(Nfft*Nsym)];
         
         %LS估计
         h_est = ifft(H_est);
         h_DFT = h_est(1:ch_length);
         H_DFT = fft(h_DFT,Nfft); 
         err=(H-H_DFT)*(H-H_DFT)';
         z2=[z2 err/(Nfft*Nsym)];  
         
         % 为MMSE估计准备信道协方差矩阵
         H_est = MMSE_CE(Y,Xp,loc,Nfft,Nps,h,SNR);
         err=(H-H_est)*(H-H_est)';
         zm=[zm err/(Nfft*Nsym)];
         
         % MMSE Estimator - DFT Based
         h_est = ifft(H_est);
         h_DFT = h_est(1:ch_length);
         H_DFT = fft(h_DFT,Nfft); 
         err=(H-H_DFT)*(H-H_DFT)';
         zms=[zms err/(Nfft*Nsym)];
     end
      % 累加每次迭代的MSE
     z_linin=z_linin+z;
     z_splin=z_splin+z1;
     z_lindft=z_lindft+z2;
     z_spldft=z_spldft+z2;
     zmmse=zmmse+zm;
     zmmse_dft=zmmse_dft+zms;
end


figure(1)
semilogy(snr1,(1/itr)*z_linin,'r+:', snr1,(1/itr)*z_splin,'bo:', snr1,(1/itr)*z_lindft,'--xb', snr1,(1/itr)*z_spldft,'--sk');
legend('LS - 线性插值','LS - 样条三次插值','LS - 线性插补(DFT)','LS - S-样条二次插值(DFT)');
xlabel('SNR');
ylabel('MSE');
grid on
hold on

figure(2)
semilogy(snr1,(1/itr)*zmmse,'r+:',snr1,(1/itr)*zmmse_dft,'bo:');
xlabel('SNR');
ylabel('MSE');
legend('MMSE','MMSE（DFT）');
hold on
grid on


figure(3)
semilogy(snr1,(1/itr)*z_linin,'r+:', snr1,(1/itr)*z_splin,'bo:', snr1, (1/itr)*zmmse,'--xk');
xlabel('SNR');
ylabel('MSE');
legend('LS - 线性插值','LS - 样条三次插值','MMSE');
hold on
grid on 
up4089

6. 仿真结果

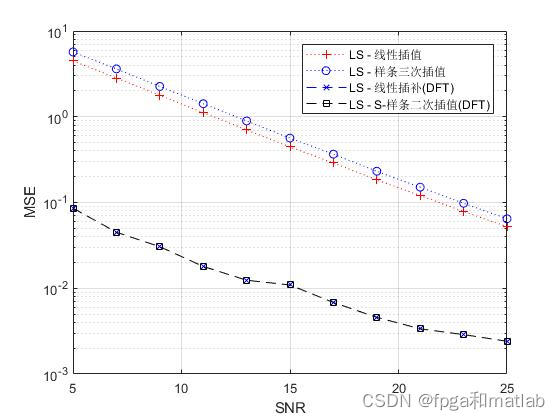
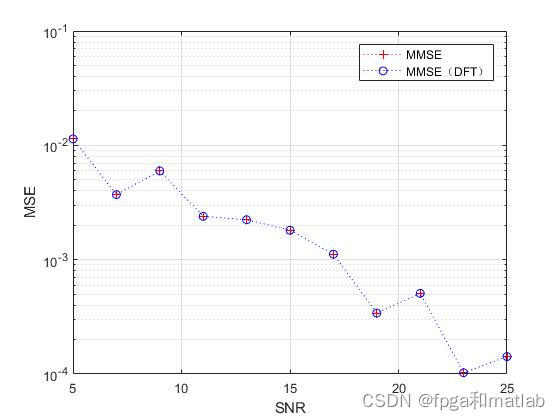
不同的信道估计方法各有优劣，LS简单直观但可能在噪声影响下表现不佳；LS插值方法提高了信道估计的连续性；Spline插值进一步提升了平滑度和精确度；而MMSE估计通过利用信道先验知识，在统计意义上提供了最优的估计性能，特别是在低信噪比环境下。选择合适的信道估计方法需综合考虑系统要求、复杂度和性能指标。