【MATLAB例程】基于Taylor迭代的二维TOA定位解算程序，锚点数量可自由设置。附代码下载链接

Taylor迭代可以在噪声复杂的情况下，取得良好的定位效果，广泛应用于TDOA的解算过程中，但如果TOA的情况下，噪声呈现非高斯，可是可以使用Taylor的，本文给出其二维平面上的例程。
参考文献：《基于Taylor-Chan算法的改进UWB室内三维定位方法》

简介

Taylor 方法（又称迭代线性化方法）用于求解非线性测距模型的最小二乘解，通过在当前估计点处对测距方程进行一阶泰勒展开，线性化后利用最小二乘（LS）迭代更新位置估计，直到收敛。

• 适用场景：锚点数目 $N\ge 3$（二维），测量为 TOA（Time of Arrival），噪声满足高斯分布近似。
• 优点：实现简单，计算量低；收敛速度与初值选取有关。
• 参考文献：《基于 Taylor–Chan 算法的改进 UWB 室内三维定位方法》。

1. 初始化

   num_stations = 4;                  % 锚点数
   std_var1 = 1e-11;                  % TOA 时间噪声标准差
   stations_position = 100*rand(num_stations,2);  
   c = 3e8;                           % 光速
   position = 5*ones(1,2)+5*randn(1,2); % 待定位真值
   

   • 随机生成 4 个锚点位置；
   • 随机生成目标真实坐标；
   • 通过 $\Delta t=\Vert \mathbf{x}-{\mathbf{s}}_i\Vert /c+{\epsilon }_i$ 构造有噪 TOA 测量。

2. TOA 测量建模

   delta   = ones(N,1)*position - stations_position;
   r_ideal = sqrt(sum(delta.^2,2));
   delta_t = r_ideal/c + std_var1*randn(size(r_ideal));
   r       = delta_t * c;
   

   • 计算理想距离 $r_i^{\text{ideal}}=\Vert \mathbf{x}-{\mathbf{s}}_i\Vert$；
   • 加入测时误差 ${\epsilon }_i\sim \mathcal{N}(0,{\sigma }_t^2)$，得到带噪测距 $r_i$。

3. 迭代线性化（Taylor 展开）

   • 初值选取：取所有锚点坐标平均值

     $${\mathbf{x}}^{(0)}=\frac{1}{N}\sum _{i=1}^N{\mathbf{s}}_i.$$

   • 第 $k$ 次迭代：

     1. 计算残差向量

        $$B_i=\Vert {\mathbf{x}}^{(k)}-{\mathbf{s}}_i\Vert -r_i,i=1,\dots ,N.$$

     2. 构造雅可比矩阵

        $$A_{i,:}=\left[\frac{x^{(k)}-s_{i,x}}{\Vert {\mathbf{x}}^{(k)}-{\mathbf{s}}_i\Vert },\frac{y^{(k)}-s_{i,y}}{\Vert {\mathbf{x}}^{(k)}-{\mathbf{s}}_i\Vert }\right].$$

     3. 线性最小二乘更新

        $$\Delta \mathbf{x}=(A^{T}A{)}^{-1}{A}^T\mathbf{B},{\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+\Delta \mathbf{x}.$$

     4. 判断收敛：$\Vert \Delta \mathbf{x}\Vert <ϵ$ 或达到最大迭代次数。

4. 结果可视化与输出

   • 绘制锚点、真实位置与迭代后估计位置；
   • 画出迭代误差随迭代次数的曲线；
   • 在命令行打印最终估计值及误差。

更多细节，见程序中的注释，具有丰富的中文注释

运行结果

4个锚点的示例

定位示意图：

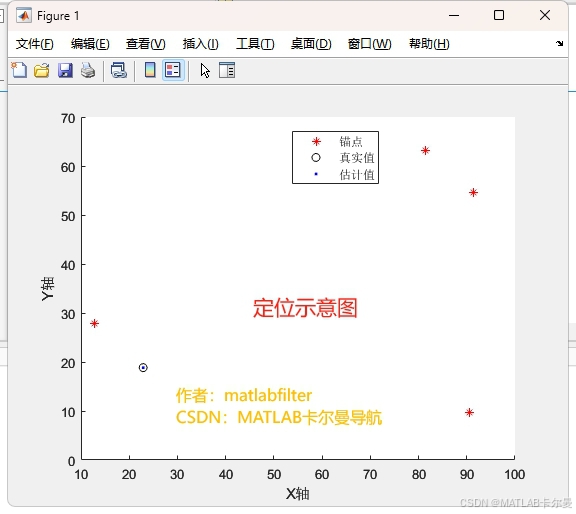
定位结果：

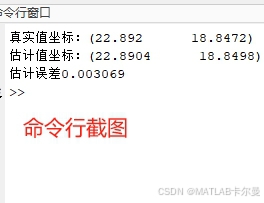
迭代时的误差曲线：

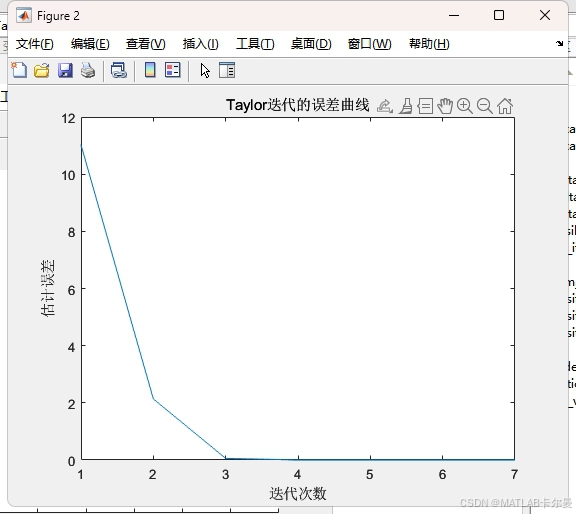
40个锚点的示例

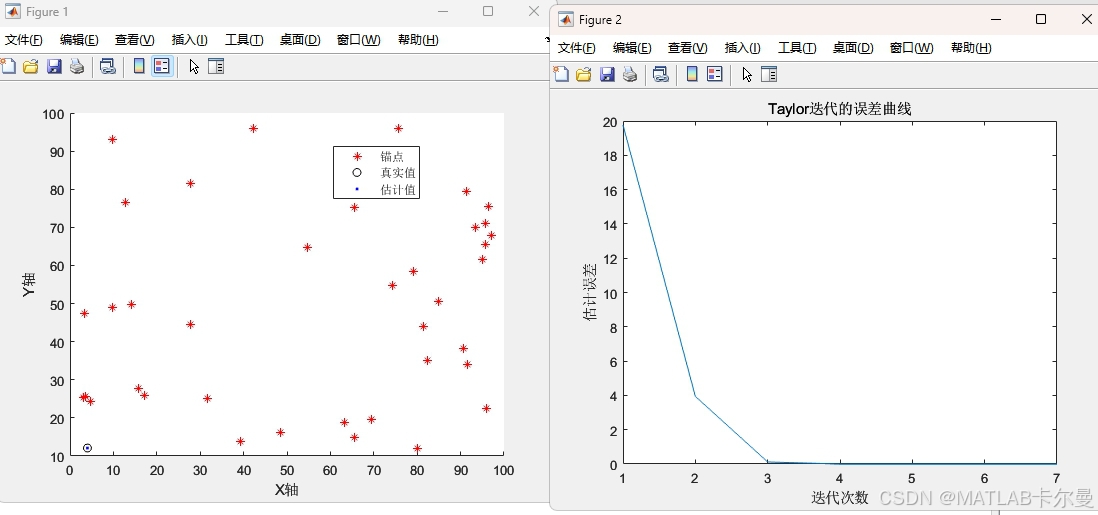
matlab源代码

部分代码如下：

% Taylor方法解算TOA，二维目标、N个锚点
% 参考文献:《基于Taylor-Chan算法的改进UWB室内三维定位方法》
% 作者：matlabfilter
% 2025-07-12/Ver1
%% 初始化
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
num_stations = 4; % 基站数量（锚点数量）
std_var1 = 1e-11; %TOA时间误差（标准差）
% 固定基站位置
stations_position = 100*rand(num_stations,2);
c = 3e8;
% 生成待定位点坐标
position = 5*ones(1,2)+5*randn(1,2);
%% TOA 建模

%% 迭代过程
% 基站均值作为初值

%% 绘图

%% 坐标输出

修改基站数量的代码：

完整代码见对应的付费专栏：https://blog.youkuaiyun.com/callmeup/article/details/149293309?spm=1011.2415.3001.5331

或单个代码的下载链接：https://download.youkuaiyun.com/download/callmeup/91359667

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者