【MATLAB例程】 基于MVC（Max Versoria Criterion）的EKF和经典EKF的对比，例程用于二维平面的运动估计|附MATLAB代码下载链接

本文介绍一种基于Versoria函数改进的扩展卡尔曼滤波（MVC-EKF）算法，与传统EKF进行对比，重点解决传统EKF在非高斯噪声条件下的鲁棒性问题。

程序介绍

算法核心创新

本代码实现了一种基于Versoria函数改进的扩展卡尔曼滤波（MVC-EKF）算法，重点解决传统EKF在非高斯噪声条件下的鲁棒性问题。主要创新体现在：

1. Versoria权重函数：通过指数型权重函数动态调整卡尔曼增益

2. 协方差迭代机制：采用Joseph形式协方差更新公式

系统模型与公式推导

状态空间模型

• 状态方程（线性运动模型）：
  $$x_{k+1}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]x_k+\left[\begin{array}{c}1\\ 2\end{array}\right]+w_k$$
  过程噪声$w_k\sim \mathcal{N}(0,Q)$, $Q=0.01I_2$

• 观测方程（非线性测量模型）：
  $$z_k=\left[\begin{array}{c}\sqrt{x_{1,k}}\\ \sqrt{x_{2,k}}\end{array}\right]+v_k$$
  观测噪声$v_k\sim \mathcal{N}(0,R)+{\delta }_{10<k<30}\cdot 10$, $R=I_2$

雅可比矩阵计算

• 状态转移雅可比矩阵：
  $$F_k=\frac{\partial f}{\partial x}=I_2$$

• 观测雅可比矩阵（关键非线性处理）：
  $$H_k=\left[\begin{array}{cc}\frac{x_1}{\sqrt{x_1^2+x_2^2}}& \frac{x_2}{\sqrt{x_1^2+x_2^2}}\\ \frac{1}{2\sqrt{x_1}}& \frac{1}{2\sqrt{x_2}}\end{array}\right]$$
  该矩阵在预测状态${\hat{x}}_k^{-}$处线性化，实现泰勒一阶近似

法实现流程

预测步骤（EKF与MVC-EKF共享）

x_pred = f(x_est(:,k-1))  
P_pred = F_k * P_est * F_k' + Q

更新步骤差异

步骤	EKF	MVC-EKF改进
卡尔曼增益	$K_k=P_{p}red{H}_k^T{S}_k^{-1}$	$K_k^{MVC}=w_{MVC}\cdot K_k$
状态更新	${\hat{x}}_k=x_{p}red+K_k{ϵ}_k$	${\hat{x}}_k^{MVC}=x_{p}red+K_k^{MVC}{ϵ}_k$
协方差更新	$P_k=(I-K_k{H}_k)P_{p}red$	$P_k^{MVC}=(I-K_k^{MVC}{H}_k)P_{p}red$

性能评估方法

代码实现多维度误差分析，包含：

1. 均方根误差（RMSE）：
   $$\text{RMSE}=\sqrt{\frac{1}{N}\sum _{k=1}^N({\hat{x}}_k-x_k^{true}{)}^2}$$
   该指标综合反映估计精度

2. 极大值误差：
   $$\text{MAX\_ERR}=\max (|{\hat{x}}_k-x_k^{true}|)$$
   反映算法在异常值冲击下的鲁棒性

3. 标准差：
   $$\text{STD}=\sqrt{\frac{1}{N-1}\sum _{k=1}^N(e_k-\bar{e}{)}^2}$$
   表征误差分布的离散程度

运行结果

状态曲线：

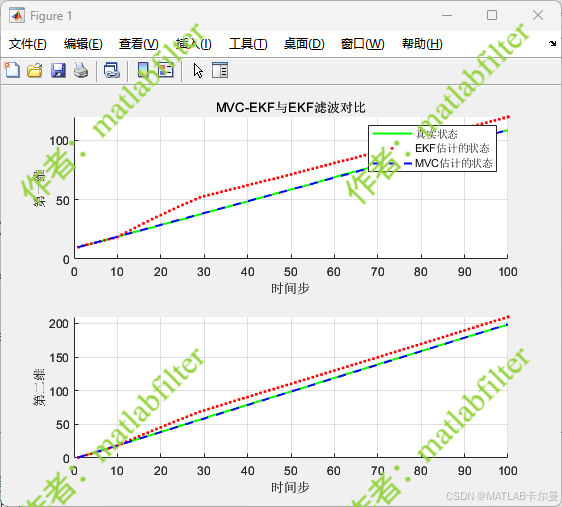
状态误差曲线：

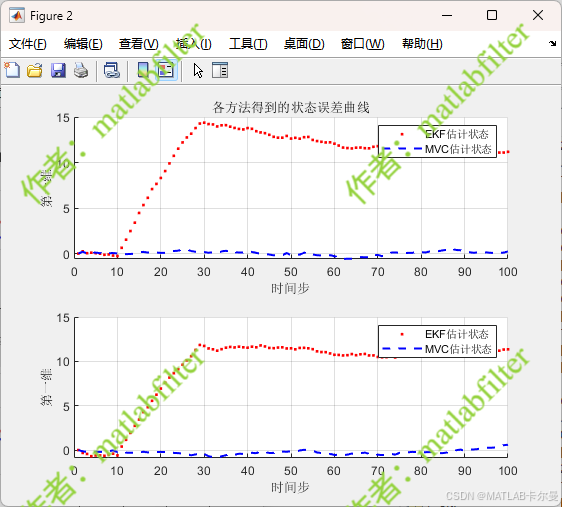
命令行的结果输出：

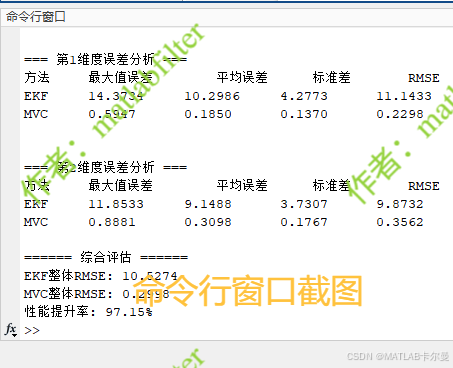
matlab代码

部分代码：

% 基于MVC的EKF，含有与EKF的对比二维平面的运动估计
% 核心：目标跟踪或状态估计，通过Versoria函数优化协方差更新
% 2025-06-21/Ver1

clear; clc; close all;
% rng(0);
%% 系统模型定义
% 定义状态空间模型
% x(k+1) = f(x(k)) + w(k)
% y(k) = h(x(k)) + v(k)

% 非线性状态转移函数
f = @(x) [x(1) + 1;  x(2) + 2];
% 非线性观测函数(距离与角度)
h = @(x) [x(1)^0.5; x(2)^0.5];

% f 和 h 的雅可比矩阵
F = @(x) [1, 0; 0, 1]; % f 的雅可比矩阵
% H = @(x) [2 * x(1), 1];     % h 的雅可比矩阵
H = @(x) [x(1)*(x(1)^2+x(2)^2)^(-0.5),x(2)*(x(1)^2+x(2)^2)^(-0.5);
    0.5*x(1)^(-0.5),0.5*x(2)^(-0.5)];     % h 的雅可比矩阵

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/91092933

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者