【MATLAB代码】基于MVC（Max Versoria Criterion）和MCC的EKF，两种算法对比，例程用于二维平面的运动估计|附代码下载链接

在这里插入图片描述

本文所述的代码实现MVC和MCC的EKF，即：通过Versoria函数（MVC）和最大相关熵准则（MCC）优化滤波器在非高斯噪声条件下的鲁棒性。系统针对二维平面运动目标跟踪场景，重点解决观测异常值干扰下的状态估计问题

文章目录

程序介绍
运行结果
MATLAB代码

程序介绍

程序包含三大核心模块：

经典EKF实现：基于线性化近似的标准滤波流程
MCC-EKF改进：通过高斯核函数抑制脉冲噪声影响
MVC-EKF创新：采用Versoria加权函数优化协方差更新策略

系统模型数学描述

状态空间模型：

% 状态转移方程（线性）
f = @(x) [x(1) + 1;  x(2) + 2];  

% 观测方程（非线性极坐标）
h = @(x) [norm(x); atan2(x(2),x(1))];

对应的雅可比矩阵推导：

H = @(x) [x(1)/r, x(2)/r;          % r = sqrt(x1²+x2²)
          -x2/(x1²+x2²), x1/(x1²+x2²)];

噪声模型：

过程噪声： $w_k \sim \mathcal{N}(0,Q)$ , $Q=0.01I_2$
观测噪声： $v_k \sim \mathcal{N}(0,R) + \delta_{10<k<30} \cdot 10$ , $R=I_2$

核心算法公式

1. 经典EKF更新方程

预测步骤：
$\begin{aligned} \hat{x}_k^- &= f(\hat{x}_{k-1}) \\ P_k^- &= F_{k-1}P_{k-1}F_{k-1}^T + Q \end{aligned}$

更新步骤：
$\begin{aligned} K_k &= P_k^- H_k^T (H_k P_k^- H_k^T + R)^{-1} \\ \hat{x}_k &= \hat{x}_k^- + K_k(z_k - h(\hat{x}_k^-)) \\ P_k &= (I - K_k H_k)P_k^- \end{aligned}$

MCC-EKF改进算法：
引入高斯核相关熵准则：

MCC = @(y, y_pred) exp(-0.5*((y - y_pred)/sigma).^2);  % σ=2

更新方程为：
$\hat{x}_k = \hat{x}_k^- + \text{diag}(w_{MCC}) \cdot K_k (z_k - h(\hat{x}_k^-))$
其中权重 $w_{MCC}$ 通过核函数计算，能有效抑制脉冲噪声

MVC：
采用Versoria加权函数优化协方差更新：

MVC = @(y, y_pred, R) exp(-0.5*(y-y_pred).^2./R);  % Versoria函数

更新过程：
$\begin{aligned} w_{MVC} &= \frac{3}{2\sigma_v^2} \left(1 + \frac{(z_k - h(\hat{x}_k^-))^2}{\sigma_v^2}\right)^{-1} \\ \hat{x}_k &= \hat{x}_k^- + w_{MVC} K_k (z_k - h(\hat{x}_k^-)) \end{aligned}$
该函数通过自适应调整增益矩阵，增强对异常值的鲁棒性

运行结果

状态曲线：
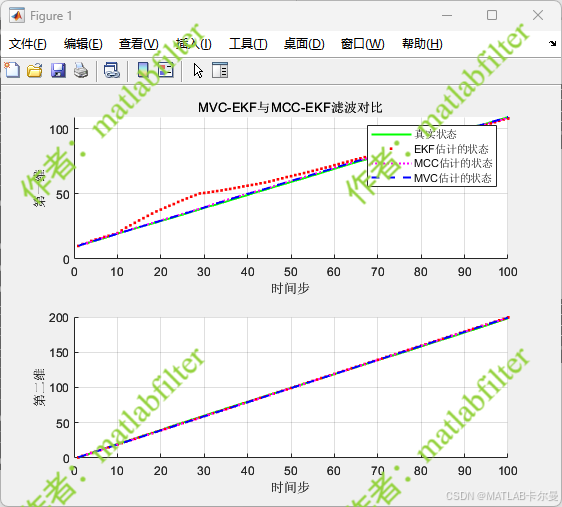
在这里插入图片描述
状态误差曲线：

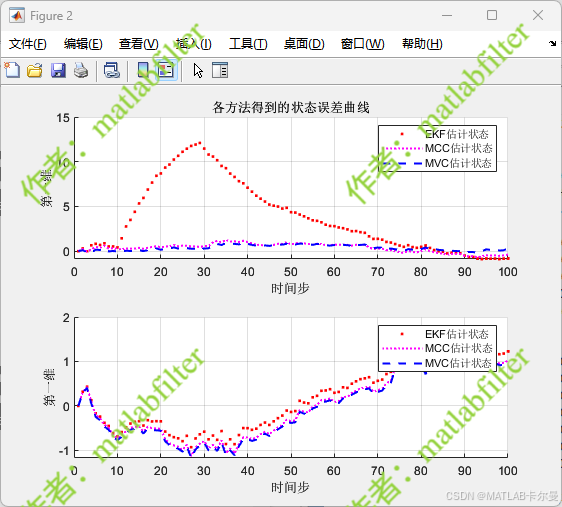
MATLAB代码

程序结构如下：
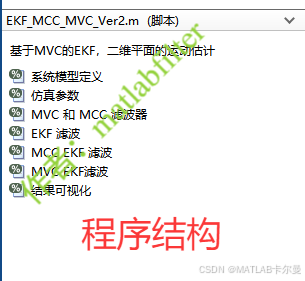
在这里插入图片描述
部分源代码：

% 基于MVC的EKF，二维平面的运动估计
% 核心：目标跟踪或状态估计，通过Versoria函数优化协方差更新
% 2025-05-08/Ver1
% 2025-06-09/Ver2：MVC和MCC的对比，修复bug

clear; clc; close all;
rng(0);
%% 系统模型定义
% 定义状态空间模型
% x(k+1) = f(x(k)) + w(k)
% y(k) = h(x(k)) + v(k)

% 非线性状态转移函数
f = @(x) [x(1) + 1;  x(2) + 2];
% 非线性观测函数(距离与角度)
h = @(x) [(x(1)^2+x(2)^2)^0.5; atan(x(2)/x(1))];

% f 和 h 的雅可比矩阵
F = @(x) [1, 0; 0, 1]; % f 的雅可比矩阵
% H = @(x) [2 * x(1), 1];     % h 的雅可比矩阵
H = @(x) [x(1)*(x(1)^2+x(2)^2)^(-0.5),x(2)*(x(1)^2+x(2)^2)^(-0.5);
    -x(2)/(x(1)^2+x(2)^2),x(1)/(x(1)^2)+x(2)^2];     % h 的雅可比矩阵

% 噪声协方差矩阵
Q = 0.01 * eye(2); % 过程噪声协方差
R = diag([1,1]);           % 测量噪声协方差

%% 仿真参数
n = 2;      % 状态维度
N = 100;     % 时间步数
x_true = zeros(n, N); % 真实状态
x_est_ekf = zeros(n, N);  % MCC 估计状态
x_est_mcc = zeros(n, N);  % MCC 估计状态
x_est_mvc = zeros(n, N);  % MVC 估计状态
y_meas = zeros(2, N);     % 测量值

% 初始状态
x_true(:, 1) = [10; 1];
x_est_ekf(:, 1) = [10; 1];
x_est_mcc(:, 1) = [10; 1];
x_est_mvc(:, 1) = [10; 1];

% 随机生成有噪声的测量值
for k = 1:N
    y_meas(:,k) = h(x_true(:, k)) + diag(sqrt(R) ).* randn;
    if 10<k && k<30
        y_meas(:,k) = h(x_true(:, k)) + diag(sqrt(R) ) * randn + 10; %特定时刻的异常值
    end
    if k < N
        x_true(:, k+1) = f(x_true(:, k)) + sqrt(Q) * randn(n, 1);

    end
end

%% MVC 和 MCC 滤波器
% 初始估计误差协方差
P_ekf = eye(n); % 经典EKF 初始误差协方差
P_mcc = eye(n); % MCC 初始误差协方差
P_mvc = eye(n); % MVC 初始误差协方差
% 定义 MCC 函数（高斯核相关熵）