【MATLAB例程】基于MCC（最大相关熵）的EKF，一维滤波，用于解决观测噪声的异常|附下载链接

最新推荐文章于 2026-01-01 21:20:54 发布

原创最新推荐文章于 2026-01-01 21:20:54 发布 · 1.2k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

卡尔曼专题免费专栏专栏收录该内容

98 篇文章

订阅专栏

在这里插入图片描述

本文所述的代码实现了一种基于最大相关熵准则（Maximum Correntropy Criterion, MCC）的鲁棒性卡尔曼滤波算法（MCC-KF），重点解决传统卡尔曼滤波在观测噪声存在异常值时估计精度下降的问题。通过引入高斯核函数对残差进行加权处理，有效降低了异常观测值对状态估计的干扰。

代码说明

函数结构：
- 代码以 mcc_kalman_filter 函数形式封装，直接运行即可生成结果。
MCC 核权重：
- 使用高斯核函数计算权重：
```
w = exp(-y^2 / (2 * sigma^2));
```
- 当残差较大时（异常值影响残差），权重 w 会减小，从而降低异常值对更新的影响。
滤波过程：
- 先预测状态和协方差：
```
x_pred = F * x_estimates(t - 1);
P_pred = F * P * F' + Q;
```
- 再根据 MCC 调整残差，计算卡尔曼增益并更新状态和协方差。
异常值处理：
- 在生成观测数据时，添加异常值：
```
noise(10:15) = noise(10:15) + 10;
```
- 通过 MCC 的核权重机制，滤波器对异常值表现出鲁棒性。
绘图结果：
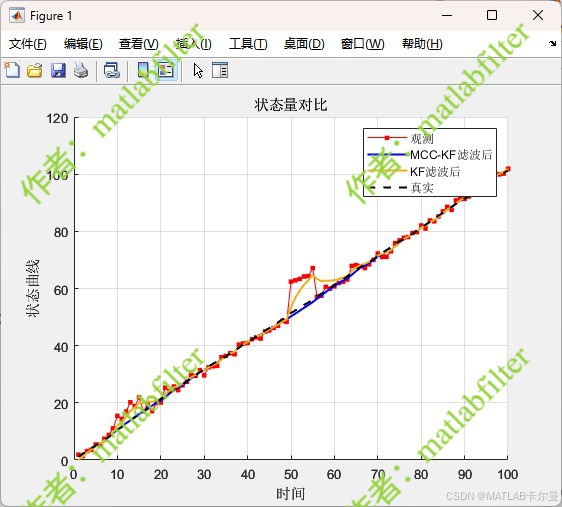
- 绘制真实状态、观测值和 MCC 卡尔曼滤波的估计值，直观显示滤波效果。

运行结果

滤波结果：
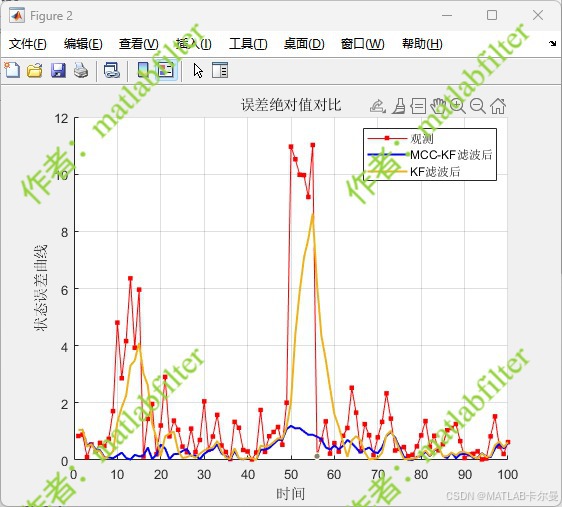
在这里插入图片描述
误差绝对值对比：

命令行截图：
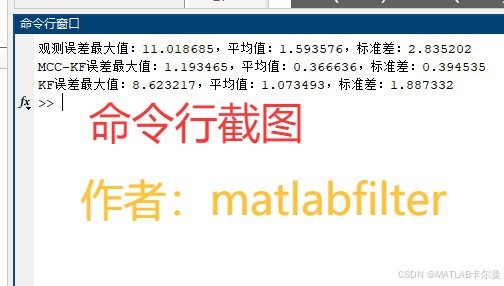
在这里插入图片描述

从图中可以观察到， $MCC$ 卡尔曼滤波能够有效抑制异常值对状态估计的影响。

MATLAB源代码

部分代码如下：

% 关于MCC（最大相关熵）的一维卡尔曼滤波例程，用于解决观测噪声的异常
% 2025-06-04/Ver1
clc;clear ;close all;
% rng(0);

%% 初始化
% 参数设置
T = 100;             % 时间步数
n = 1;              % 状态维度
m = 1;              % 观测维度
sigma = 2;        % 高斯核的带宽参数

% 系统模型
F = 1;              % 状态转移矩阵
H = 1;              % 观测矩阵
Q = 0.1;           % 过程噪声协方差
R = 1;              % 观测噪声协方差

% 初始状态
x0 = 0;             % 初始状态
P0 = 1;             % 初始协方差

% 生成观测数据（含异常值）
true_state = cumsum(randn(T, 1) * 0.1) + [1:T]'; % 真实状态
noise = randn(T, 1);                    % 观测噪声
noise(10:15) = noise(10:15) + 5;       % 添加异常值
noise(50:55) = noise(50:55) + 10;       % 添加异常值
z = true_state + noise;                 % 观测值

% 初始化卡尔曼滤波
x_est_MCCKF = zeros(T, 1);  % 保存状态估计
x_est_MCCKF(1) = x0;        % 初始状态估计
x_est_KF = zeros(T, 1);  % 保存状态估计